
Question Number 11606 by Joel576 last updated on 29/Mar/17
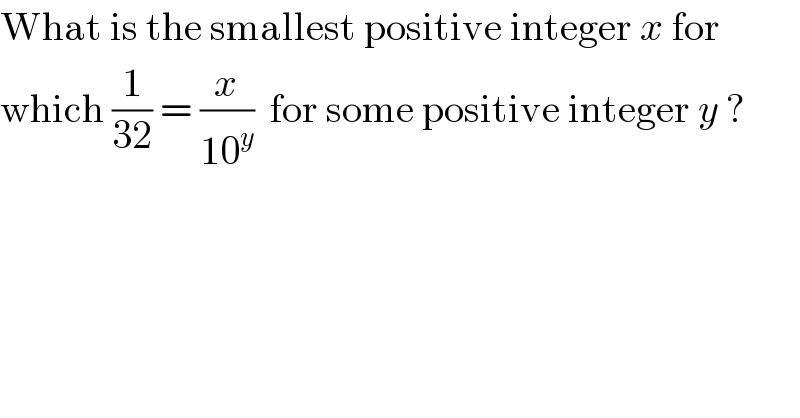
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{positive}\:\mathrm{integer}\:{x}\:\mathrm{for} \\ $$$$\mathrm{which}\:\frac{\mathrm{1}}{\mathrm{32}}\:=\:\frac{{x}}{\mathrm{10}^{{y}} }\:\:\mathrm{for}\:\mathrm{some}\:\mathrm{positive}\:\mathrm{integer}\:{y}\:? \\ $$
Answered by mrW1 last updated on 29/Mar/17
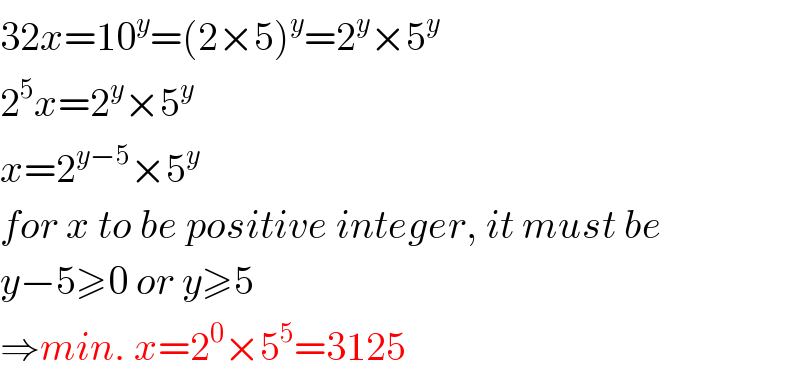
$$\mathrm{32}{x}=\mathrm{10}^{{y}} =\left(\mathrm{2}×\mathrm{5}\right)^{{y}} =\mathrm{2}^{{y}} ×\mathrm{5}^{{y}} \\ $$$$\mathrm{2}^{\mathrm{5}} {x}=\mathrm{2}^{{y}} ×\mathrm{5}^{{y}} \\ $$$${x}=\mathrm{2}^{{y}−\mathrm{5}} ×\mathrm{5}^{{y}} \\ $$$${for}\:{x}\:{to}\:{be}\:{positive}\:{integer},\:{it}\:{must}\:{be} \\ $$$${y}−\mathrm{5}\geqslant\mathrm{0}\:{or}\:{y}\geqslant\mathrm{5} \\ $$$$\Rightarrow{min}.\:{x}=\mathrm{2}^{\mathrm{0}} ×\mathrm{5}^{\mathrm{5}} =\mathrm{3125} \\ $$
