
Previous in Differential Equation Next in Differential Equation
Question Number 116054 by Study last updated on 30/Sep/20
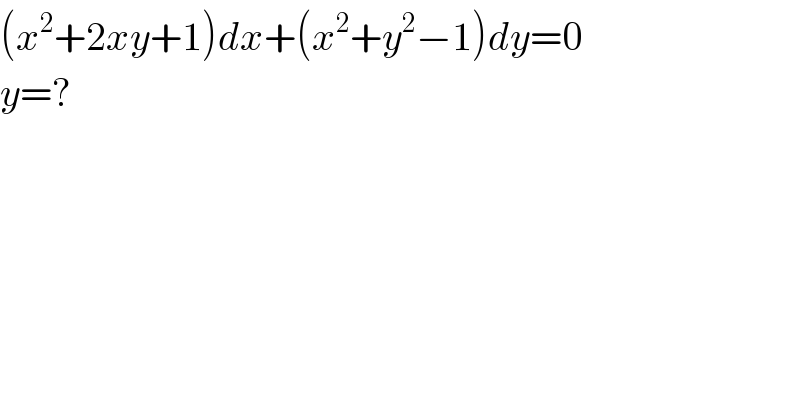
$$\left({x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{1}\right){dx}+\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}\right){dy}=\mathrm{0} \\ $$$${y}=? \\ $$
Commented by mohammad17 last updated on 30/Sep/20
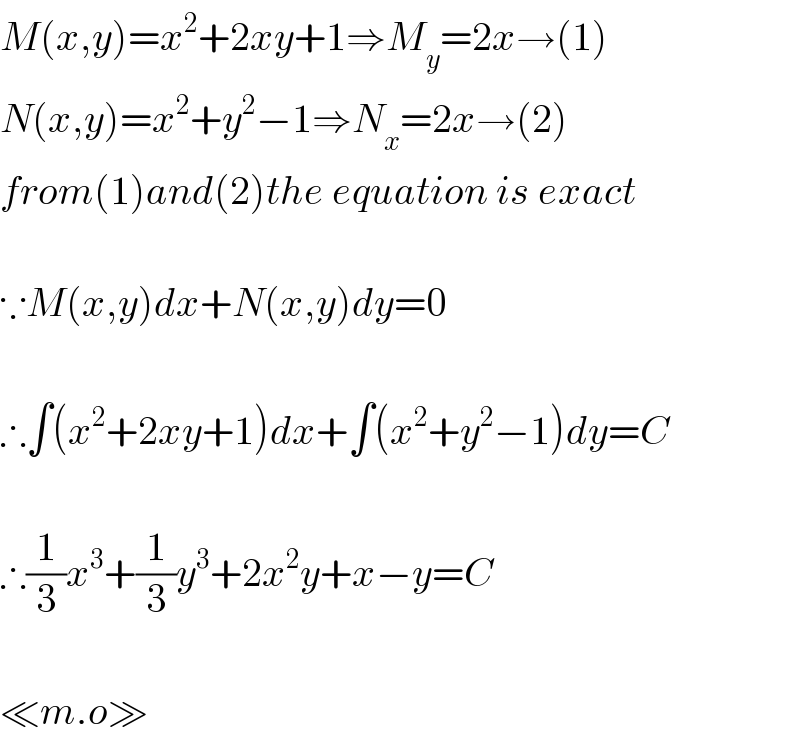
$${M}\left({x},{y}\right)={x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{1}\Rightarrow{M}_{{y}} =\mathrm{2}{x}\rightarrow\left(\mathrm{1}\right) \\ $$$${N}\left({x},{y}\right)={x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}\Rightarrow{N}_{{x}} =\mathrm{2}{x}\rightarrow\left(\mathrm{2}\right) \\ $$$${from}\left(\mathrm{1}\right){and}\left(\mathrm{2}\right){the}\:{equation}\:{is}\:{exact} \\ $$$$ \\ $$$$\because{M}\left({x},{y}\right){dx}+{N}\left({x},{y}\right){dy}=\mathrm{0} \\ $$$$ \\ $$$$\therefore\int\left({x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{1}\right){dx}+\int\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{1}\right){dy}={C} \\ $$$$ \\ $$$$\therefore\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{3}}{y}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} {y}+{x}−{y}={C} \\ $$$$ \\ $$$$\ll{m}.{o}\gg \\ $$
Answered by MWSuSon last updated on 30/Sep/20
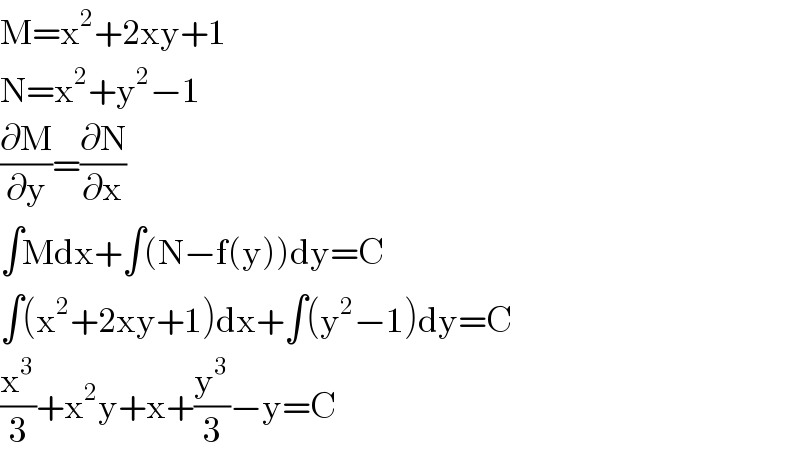
$$\mathrm{M}=\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{1} \\ $$$$\mathrm{N}=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{1} \\ $$$$\frac{\partial\mathrm{M}}{\partial\mathrm{y}}=\frac{\partial\mathrm{N}}{\partial\mathrm{x}} \\ $$$$\int\mathrm{Mdx}+\int\left(\mathrm{N}−\mathrm{f}\left(\mathrm{y}\right)\right)\mathrm{dy}=\mathrm{C} \\ $$$$\int\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2xy}+\mathrm{1}\right)\mathrm{dx}+\int\left(\mathrm{y}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{dy}=\mathrm{C} \\ $$$$\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{x}+\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{y}=\mathrm{C} \\ $$
