
Question Number 115910 by Eric002 last updated on 29/Sep/20
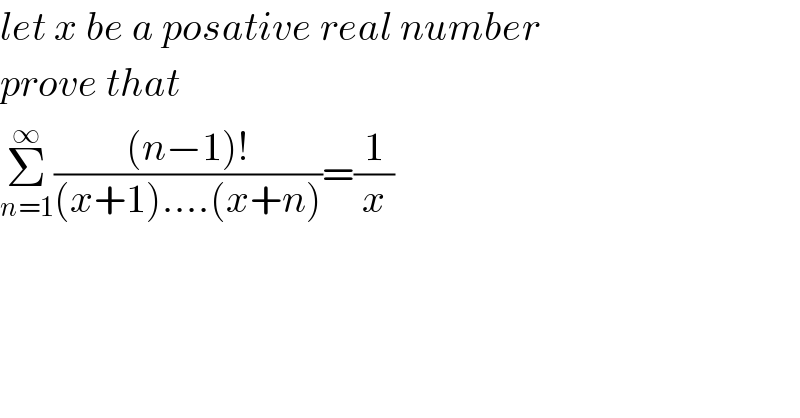
$${let}\:{x}\:{be}\:{a}\:{posative}\:{real}\:{number} \\ $$$${prove}\:{that} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({n}−\mathrm{1}\right)!}{\left({x}+\mathrm{1}\right)....\left({x}+{n}\right)}=\frac{\mathrm{1}}{{x}} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Sep/20
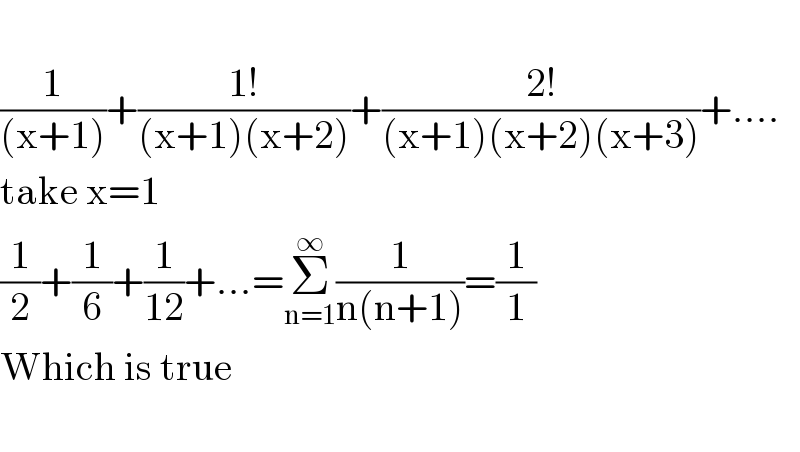
$$ \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{1}!}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)}+\frac{\mathrm{2}!}{\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{3}\right)}+.... \\ $$$$\mathrm{take}\:\mathrm{x}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{12}}+...=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{1}} \\ $$$$\mathrm{Which}\:\mathrm{is}\:\mathrm{true} \\ $$$$ \\ $$
