
Question Number 115896 by bemath last updated on 29/Sep/20
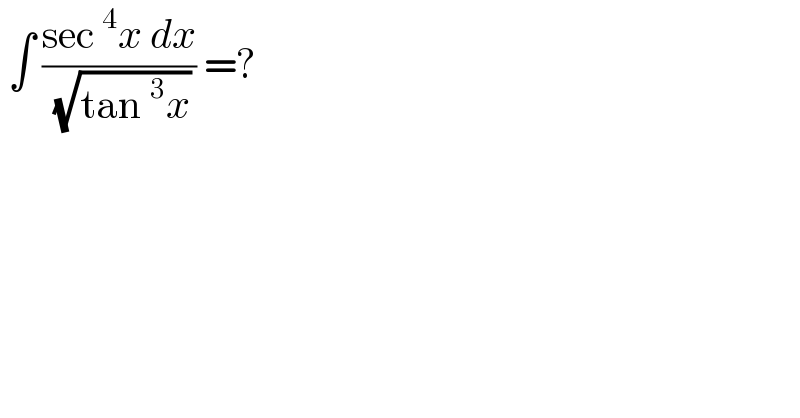
$$\:\int\:\frac{\mathrm{sec}\:^{\mathrm{4}} {x}\:{dx}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{3}} {x}}}\:=? \\ $$
Answered by TANMAY PANACEA last updated on 29/Sep/20
![∫(((1+t^2 )dt)/t^(3/2) ) [t=tanx (dt/dx)=sec^2 x] ∫t^(−(3/2)) +t^(1/2) dt =(t^(−(1/2)) /((−1)/2))+(t^(3/2) /(3/2))+c =−2(tanx)^((−1)/2) +(2/3)(tanx)^(3/2) +C](Q115900.png)
$$\int\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}}{{t}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:\:\:\left[{t}={tanx}\:\:\:\:\:\:\frac{{dt}}{{dx}}={sec}^{\mathrm{2}} {x}\right] \\ $$$$\int{t}^{−\frac{\mathrm{3}}{\mathrm{2}}} +{t}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:{dt} \\ $$$$=\frac{{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\frac{−\mathrm{1}}{\mathrm{2}}}+\frac{{t}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\frac{\mathrm{3}}{\mathrm{2}}}+{c} \\ $$$$=−\mathrm{2}\left({tanx}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} +\frac{\mathrm{2}}{\mathrm{3}}\left({tanx}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{C} \\ $$$$ \\ $$
Commented by bemath last updated on 29/Sep/20

$${thank}\:{you}\:{sir} \\ $$
Answered by Ar Brandon last updated on 29/Sep/20
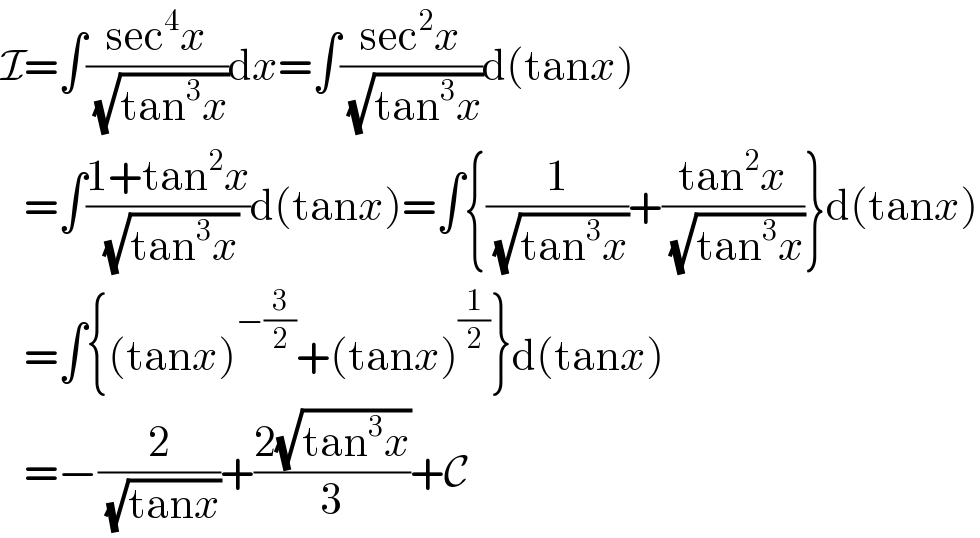
$$\mathcal{I}=\int\frac{\mathrm{sec}^{\mathrm{4}} {x}}{\:\sqrt{\mathrm{tan}^{\mathrm{3}} {x}}}\mathrm{d}{x}=\int\frac{\mathrm{sec}^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}^{\mathrm{3}} {x}}}\mathrm{d}\left(\mathrm{tan}{x}\right) \\ $$$$\:\:\:=\int\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}^{\mathrm{3}} {x}}}\mathrm{d}\left(\mathrm{tan}{x}\right)=\int\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}^{\mathrm{3}} {x}}}+\frac{\mathrm{tan}^{\mathrm{2}} {x}}{\:\sqrt{\mathrm{tan}^{\mathrm{3}} {x}}}\right\}\mathrm{d}\left(\mathrm{tan}{x}\right) \\ $$$$\:\:\:=\int\left\{\left(\mathrm{tan}{x}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} +\left(\mathrm{tan}{x}\right)_{} ^{\frac{\mathrm{1}}{\mathrm{2}}} \right\}\mathrm{d}\left(\mathrm{tan}{x}\right) \\ $$$$\:\:\:=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{tan}{x}}}+\frac{\mathrm{2}\sqrt{\mathrm{tan}^{\mathrm{3}} {x}}}{\mathrm{3}}+\mathcal{C} \\ $$
