
Question Number 115871 by bemath last updated on 29/Sep/20
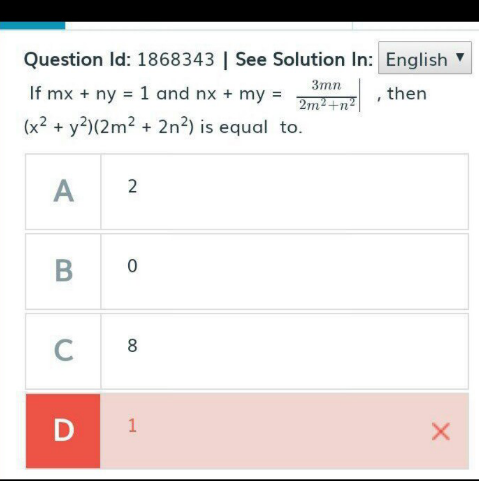
Commented by bemath last updated on 29/Sep/20
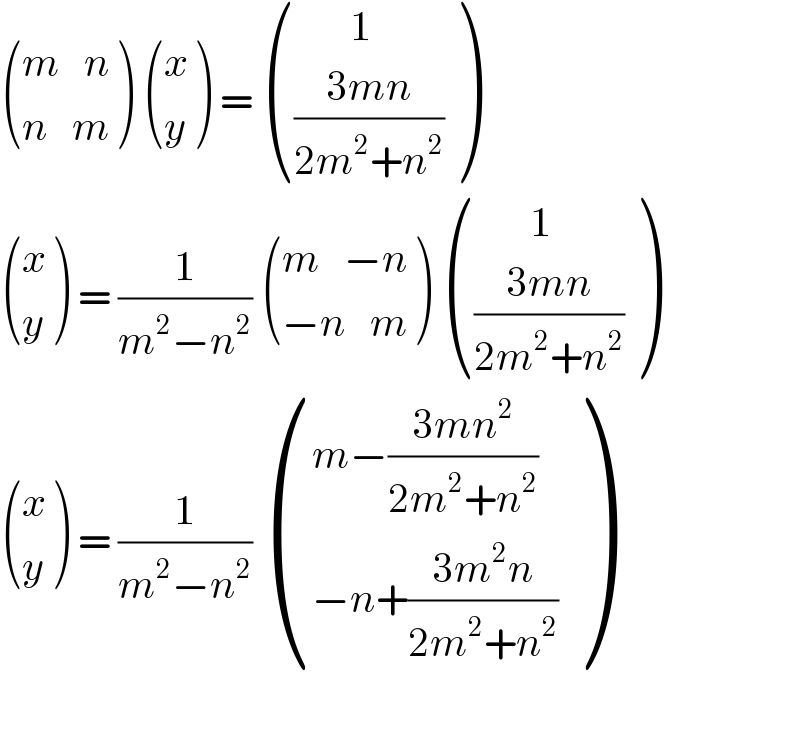
$$\begin{pmatrix}{{m}\:\:\:{n}}\\{{n}\:\:\:{m}}\end{pmatrix}\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\begin{pmatrix}{\:\:\:\:\:\:\:\mathrm{1}}\\{\frac{\mathrm{3}{mn}}{\mathrm{2}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }}\end{pmatrix} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:\begin{pmatrix}{{m}\:\:\:−{n}}\\{−{n}\:\:\:{m}}\end{pmatrix}\:\begin{pmatrix}{\:\:\:\:\:\:\:\mathrm{1}}\\{\frac{\mathrm{3}{mn}}{\mathrm{2}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }}\end{pmatrix} \\ $$$$\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{{m}^{\mathrm{2}} −{n}^{\mathrm{2}} }\:\begin{pmatrix}{{m}−\frac{\mathrm{3}{mn}^{\mathrm{2}} }{\mathrm{2}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }}\\{−{n}+\frac{\mathrm{3}{m}^{\mathrm{2}} {n}}{\mathrm{2}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }}\end{pmatrix} \\ $$$$ \\ $$
Answered by MJS_new last updated on 29/Sep/20

$${mx}+{ny}=\mathrm{1} \\ $$$${nx}+{my}=\frac{\mathrm{3}{mn}}{\mathrm{2}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{2}{m}}{\mathrm{2}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} }\wedge{y}=\frac{{n}}{\mathrm{2}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left(\mathrm{2}{m}^{\mathrm{2}} +\mathrm{2}{n}^{\mathrm{2}} \right)=\frac{\mathrm{2}\left({m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)\left(\mathrm{4}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)}{\left(\mathrm{2}{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)^{\mathrm{2}} }=\alpha \\ $$$$\mathrm{transforming}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{4}{m}^{\mathrm{4}} +\frac{\mathrm{2}\left(\mathrm{2}\alpha−\mathrm{5}\right)}{\alpha−\mathrm{2}}{m}^{\mathrm{2}} {n}^{\mathrm{2}} +{n}^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{let}\:{m}=\frac{\sqrt{\mathrm{2}{p}}}{\mathrm{2}}\wedge{n}=\sqrt{{q}};\:{p},\:{q}\:\geqslant\mathrm{0} \\ $$$${p}^{\mathrm{2}} +\frac{\mathrm{2}\alpha−\mathrm{5}}{\alpha−\mathrm{2}}{pq}+{q}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({p}+{q}\right)^{\mathrm{2}} =\frac{{pq}}{\alpha−\mathrm{2}}\wedge\left({p}−{q}\right)^{\mathrm{2}} =−\frac{\mathrm{4}\alpha−\mathrm{9}}{\alpha−\mathrm{2}}{pq} \\ $$$$\Rightarrow\:\alpha\neq\mathrm{2}\wedge\frac{\mathrm{1}}{\alpha−\mathrm{2}}\geqslant\mathrm{0}\wedge−\frac{\mathrm{4}\alpha−\mathrm{9}}{\alpha−\mathrm{2}}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}<\alpha\leqslant\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{but}\:\mathrm{maybe}\:\mathrm{I}'\mathrm{m}\:\mathrm{wrong}... \\ $$
Commented by MJS_new last updated on 29/Sep/20
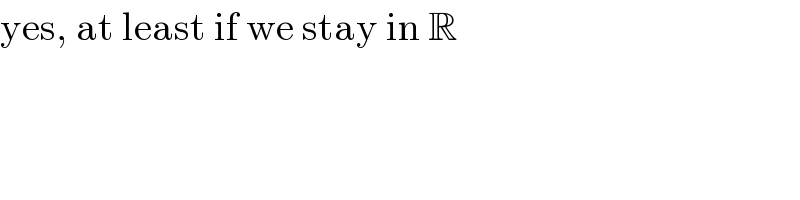
$$\mathrm{yes},\:\mathrm{at}\:\mathrm{least}\:\mathrm{if}\:\mathrm{we}\:\mathrm{stay}\:\mathrm{in}\:\mathbb{R} \\ $$
Commented by bemath last updated on 29/Sep/20
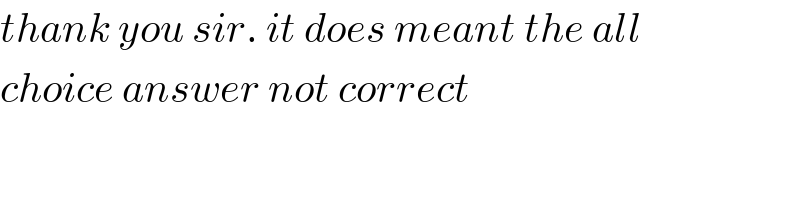
$${thank}\:{you}\:{sir}.\:{it}\:{does}\:{meant}\:{the}\:{all}\: \\ $$$${choice}\:{answer}\:{not}\:{correct} \\ $$
