
Question Number 115859 by bemath last updated on 29/Sep/20

$${Determine},\:{in}\:{simplest}\:{form}\:{the} \\ $$$${smallest}\:{of}\:{the}\:{three}\:{numbers}\:{x}, \\ $$$${y}\:{and}\:{z}\:{which}\:{satisfy}\:{the}\:{system} \\ $$$$\begin{cases}{\mathrm{log}\:_{\mathrm{9}} \left({x}\right)+\mathrm{log}\:_{\mathrm{9}} \left({y}\right)+\mathrm{log}\:_{\mathrm{3}} \left({z}\right)=\mathrm{2}}\\{\mathrm{log}\:_{\mathrm{16}} \left({x}\right)+\mathrm{log}\:_{\mathrm{4}} \left({y}\right)+\mathrm{log}\:_{\mathrm{16}} \left({z}\right)=\mathrm{1}}\\{\mathrm{log}\:_{\mathrm{5}} \left({x}\right)+\mathrm{log}\:_{\mathrm{25}} \left({y}\right)+\mathrm{log}\:_{\mathrm{25}} \left({z}\right)=\mathrm{0}}\end{cases} \\ $$
Answered by bobhans last updated on 29/Sep/20
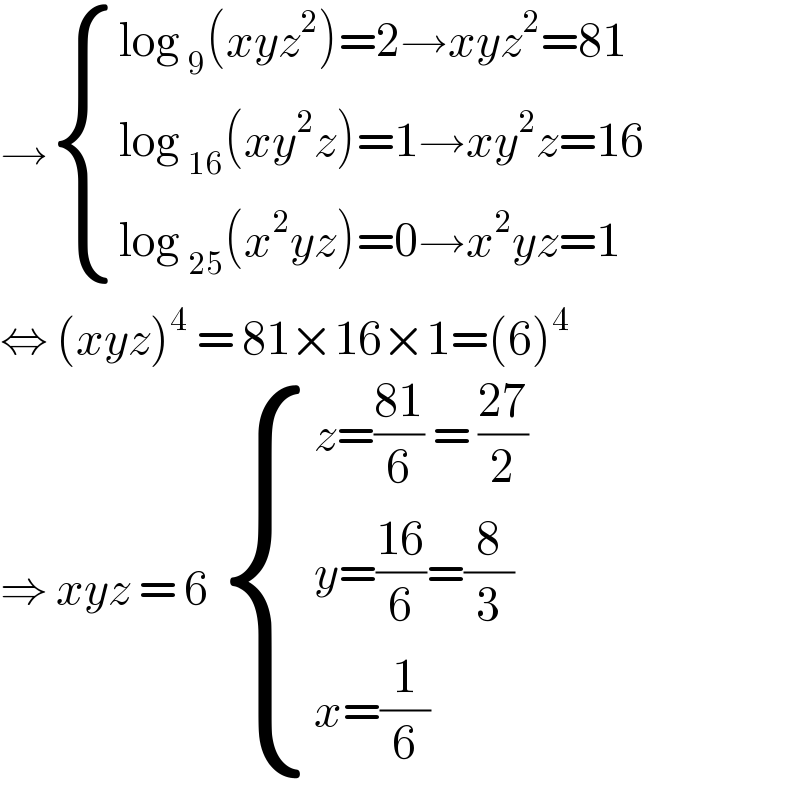
$$\rightarrow\begin{cases}{\mathrm{log}\:_{\mathrm{9}} \left({xyz}^{\mathrm{2}} \right)=\mathrm{2}\rightarrow{xyz}^{\mathrm{2}} =\mathrm{81}}\\{\mathrm{log}\:_{\mathrm{16}} \left({xy}^{\mathrm{2}} {z}\right)=\mathrm{1}\rightarrow{xy}^{\mathrm{2}} {z}=\mathrm{16}}\\{\mathrm{log}\:_{\mathrm{25}} \left({x}^{\mathrm{2}} {yz}\right)=\mathrm{0}\rightarrow{x}^{\mathrm{2}} {yz}=\mathrm{1}}\end{cases} \\ $$$$\Leftrightarrow\:\left({xyz}\right)^{\mathrm{4}} \:=\:\mathrm{81}×\mathrm{16}×\mathrm{1}=\left(\mathrm{6}\right)^{\mathrm{4}} \\ $$$$\Rightarrow\:{xyz}\:=\:\mathrm{6}\:\begin{cases}{{z}=\frac{\mathrm{81}}{\mathrm{6}}\:=\:\frac{\mathrm{27}}{\mathrm{2}}}\\{{y}=\frac{\mathrm{16}}{\mathrm{6}}=\frac{\mathrm{8}}{\mathrm{3}}}\\{{x}=\frac{\mathrm{1}}{\mathrm{6}}}\end{cases} \\ $$
Answered by floor(10²Eta[1]) last updated on 29/Sep/20
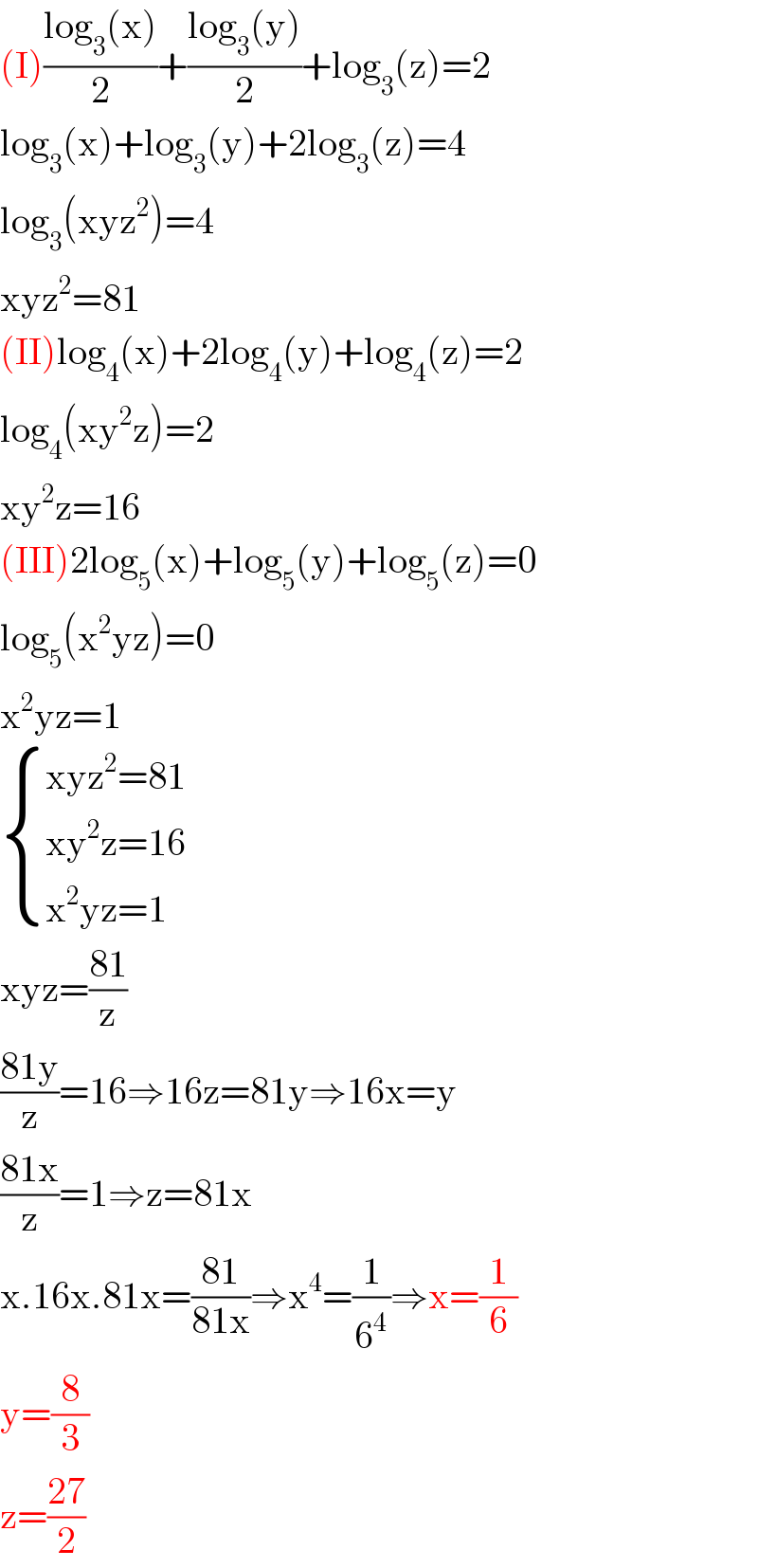
$$\left(\mathrm{I}\right)\frac{\mathrm{log}_{\mathrm{3}} \left(\mathrm{x}\right)}{\mathrm{2}}+\frac{\mathrm{log}_{\mathrm{3}} \left(\mathrm{y}\right)}{\mathrm{2}}+\mathrm{log}_{\mathrm{3}} \left(\mathrm{z}\right)=\mathrm{2} \\ $$$$\mathrm{log}_{\mathrm{3}} \left(\mathrm{x}\right)+\mathrm{log}_{\mathrm{3}} \left(\mathrm{y}\right)+\mathrm{2log}_{\mathrm{3}} \left(\mathrm{z}\right)=\mathrm{4} \\ $$$$\mathrm{log}_{\mathrm{3}} \left(\mathrm{xyz}^{\mathrm{2}} \right)=\mathrm{4} \\ $$$$\mathrm{xyz}^{\mathrm{2}} =\mathrm{81} \\ $$$$\left(\mathrm{II}\right)\mathrm{log}_{\mathrm{4}} \left(\mathrm{x}\right)+\mathrm{2log}_{\mathrm{4}} \left(\mathrm{y}\right)+\mathrm{log}_{\mathrm{4}} \left(\mathrm{z}\right)=\mathrm{2} \\ $$$$\mathrm{log}_{\mathrm{4}} \left(\mathrm{xy}^{\mathrm{2}} \mathrm{z}\right)=\mathrm{2} \\ $$$$\mathrm{xy}^{\mathrm{2}} \mathrm{z}=\mathrm{16} \\ $$$$\left(\mathrm{III}\right)\mathrm{2log}_{\mathrm{5}} \left(\mathrm{x}\right)+\mathrm{log}_{\mathrm{5}} \left(\mathrm{y}\right)+\mathrm{log}_{\mathrm{5}} \left(\mathrm{z}\right)=\mathrm{0} \\ $$$$\mathrm{log}_{\mathrm{5}} \left(\mathrm{x}^{\mathrm{2}} \mathrm{yz}\right)=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} \mathrm{yz}=\mathrm{1} \\ $$$$\begin{cases}{\mathrm{xyz}^{\mathrm{2}} =\mathrm{81}}\\{\mathrm{xy}^{\mathrm{2}} \mathrm{z}=\mathrm{16}}\\{\mathrm{x}^{\mathrm{2}} \mathrm{yz}=\mathrm{1}}\end{cases} \\ $$$$\mathrm{xyz}=\frac{\mathrm{81}}{\mathrm{z}} \\ $$$$\frac{\mathrm{81y}}{\mathrm{z}}=\mathrm{16}\Rightarrow\mathrm{16z}=\mathrm{81y}\Rightarrow\mathrm{16x}=\mathrm{y} \\ $$$$\frac{\mathrm{81x}}{\mathrm{z}}=\mathrm{1}\Rightarrow\mathrm{z}=\mathrm{81x} \\ $$$$\mathrm{x}.\mathrm{16x}.\mathrm{81x}=\frac{\mathrm{81}}{\mathrm{81x}}\Rightarrow\mathrm{x}^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{4}} }\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{y}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\mathrm{z}=\frac{\mathrm{27}}{\mathrm{2}} \\ $$
