
Question Number 115793 by ZiYangLee last updated on 28/Sep/20
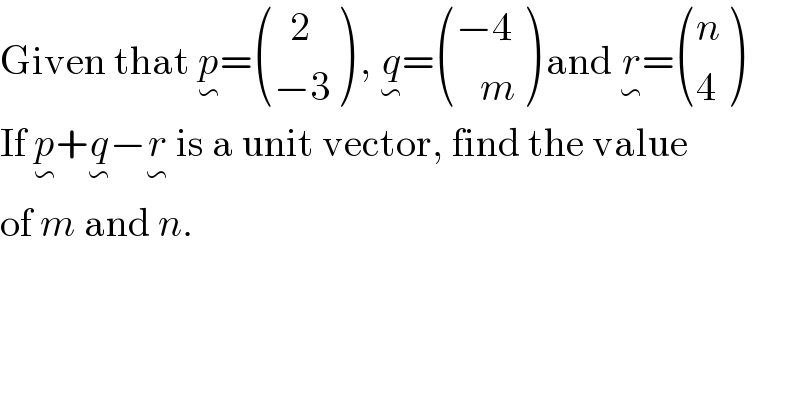
$$\mathrm{Given}\:\mathrm{that}\:\underset{\backsim} {{p}}=\begin{pmatrix}{\:\:\mathrm{2}}\\{−\mathrm{3}}\end{pmatrix}\:,\:\underset{\backsim} {{q}}=\begin{pmatrix}{−\mathrm{4}}\\{\:\:\:{m}}\end{pmatrix}\:\mathrm{and}\:\underset{\backsim} {{r}}=\begin{pmatrix}{{n}}\\{\mathrm{4}}\end{pmatrix} \\ $$$$\mathrm{If}\:\underset{\backsim} {{p}}+\underset{\backsim} {{q}}−\underset{\backsim} {{r}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{unit}\:\mathrm{vector},\:\mathrm{find}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:{m}\:\mathrm{and}\:{n}. \\ $$
Answered by $@y@m last updated on 29/Sep/20
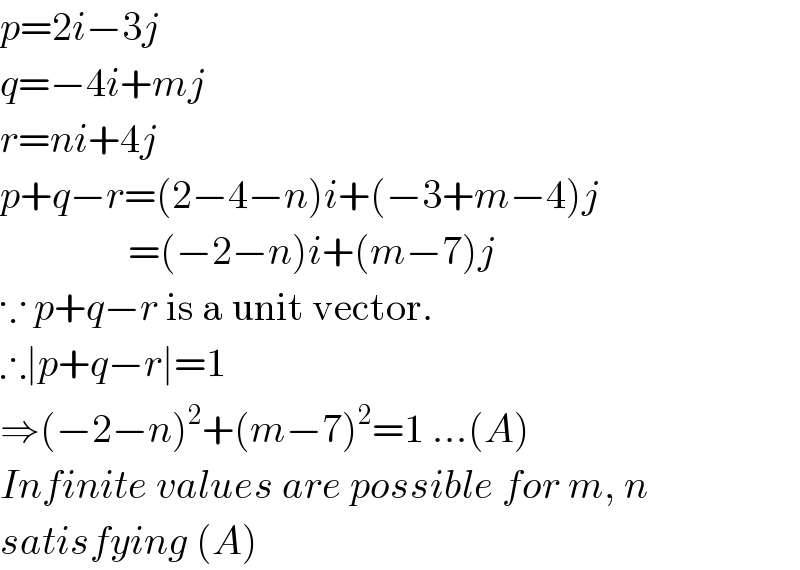
$${p}=\mathrm{2}{i}−\mathrm{3}{j} \\ $$$${q}=−\mathrm{4}{i}+{mj} \\ $$$${r}={ni}+\mathrm{4}{j} \\ $$$${p}+{q}−{r}=\left(\mathrm{2}−\mathrm{4}−{n}\right){i}+\left(−\mathrm{3}+{m}−\mathrm{4}\right){j} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−\mathrm{2}−{n}\right){i}+\left({m}−\mathrm{7}\right){j} \\ $$$$\because\:{p}+{q}−{r}\:\mathrm{is}\:\mathrm{a}\:\mathrm{unit}\:\mathrm{vector}. \\ $$$$\therefore\mid{p}+{q}−{r}\mid=\mathrm{1} \\ $$$$\Rightarrow\left(−\mathrm{2}−{n}\right)^{\mathrm{2}} +\left({m}−\mathrm{7}\right)^{\mathrm{2}} =\mathrm{1}\:...\left({A}\right) \\ $$$${Infinite}\:{values}\:{are}\:{possible}\:{for}\:{m},\:{n} \\ $$$${satisfying}\:\left({A}\right) \\ $$
Commented by ZiYangLee last updated on 29/Sep/20

$$\mathrm{Hmmm}... \\ $$
Commented by ZiYangLee last updated on 05/Oct/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$
