
Question Number 115780 by bemath last updated on 28/Sep/20
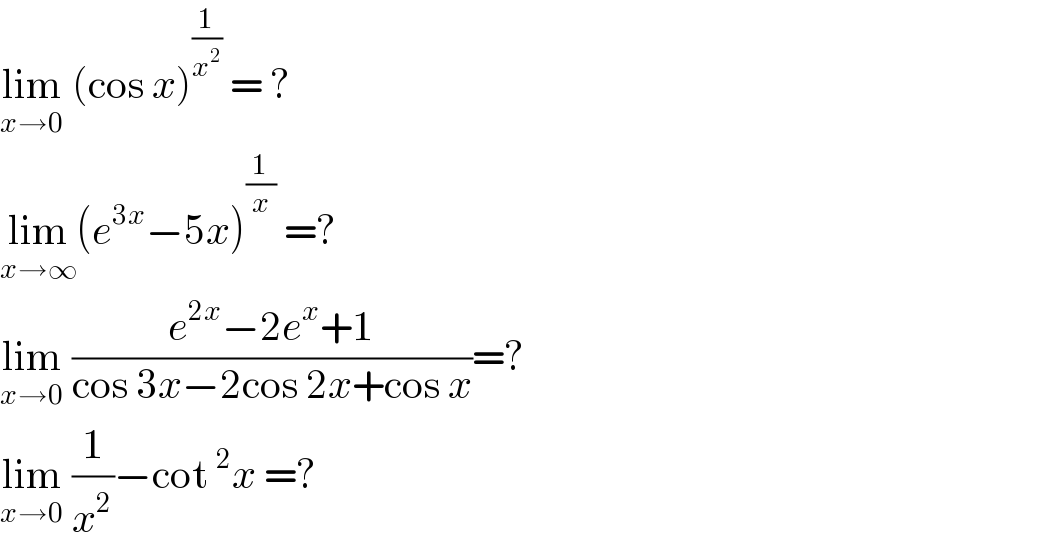
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{cos}\:{x}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\:? \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({e}^{\mathrm{3}{x}} −\mathrm{5}{x}\right)^{\frac{\mathrm{1}}{{x}}} \:=? \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{\mathrm{2}{x}} −\mathrm{2}{e}^{{x}} +\mathrm{1}}{\mathrm{cos}\:\mathrm{3}{x}−\mathrm{2cos}\:\mathrm{2}{x}+\mathrm{cos}\:{x}}=? \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{cot}\:^{\mathrm{2}} {x}\:=? \\ $$
Commented by bobhans last updated on 28/Sep/20
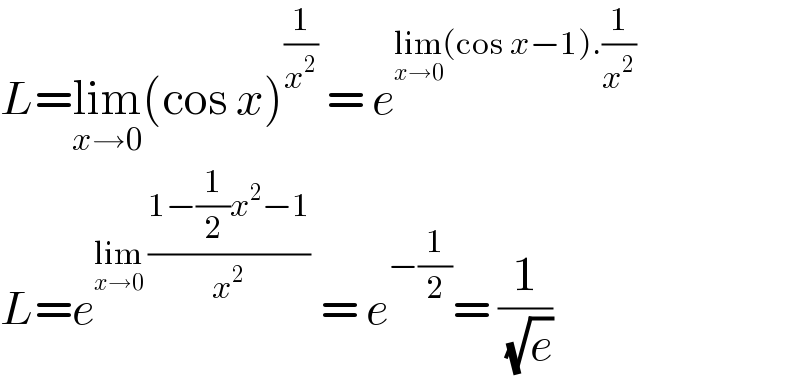
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{cos}\:{x}\right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{cos}\:{x}−\mathrm{1}\right).\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$${L}={e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} }} \:=\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\:\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Sep/20
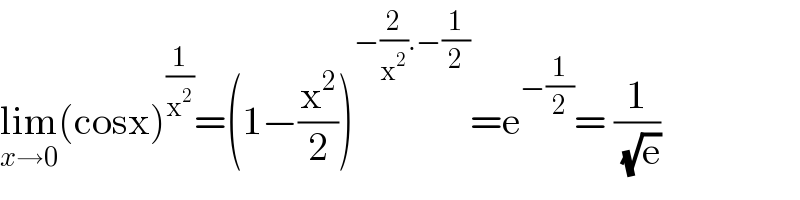
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{cosx}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} =\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{−\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{2}} }.−\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{e}}} \\ $$
Answered by bobhans last updated on 28/Sep/20
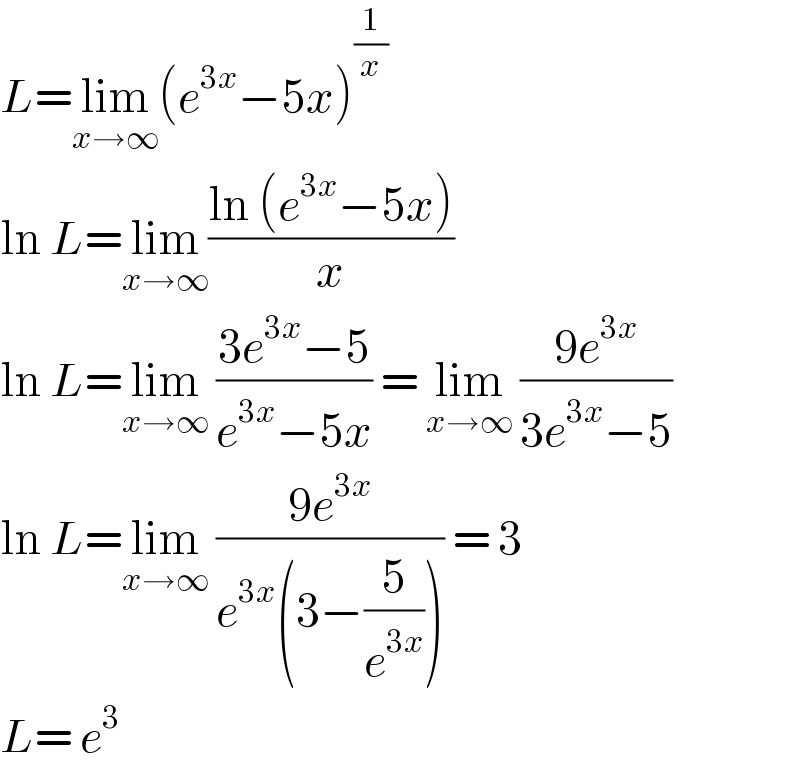
$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({e}^{\mathrm{3}{x}} −\mathrm{5}{x}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$\mathrm{ln}\:{L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\:\left({e}^{\mathrm{3}{x}} −\mathrm{5}{x}\right)}{{x}} \\ $$$$\mathrm{ln}\:{L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}{e}^{\mathrm{3}{x}} −\mathrm{5}}{{e}^{\mathrm{3}{x}} −\mathrm{5}{x}}\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{9}{e}^{\mathrm{3}{x}} }{\mathrm{3}{e}^{\mathrm{3}{x}} −\mathrm{5}} \\ $$$$\mathrm{ln}\:{L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{9}{e}^{\mathrm{3}{x}} }{{e}^{\mathrm{3}{x}} \left(\mathrm{3}−\frac{\mathrm{5}}{{e}^{\mathrm{3}{x}} }\right)}\:=\:\mathrm{3} \\ $$$${L}=\:{e}^{\mathrm{3}} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Sep/20
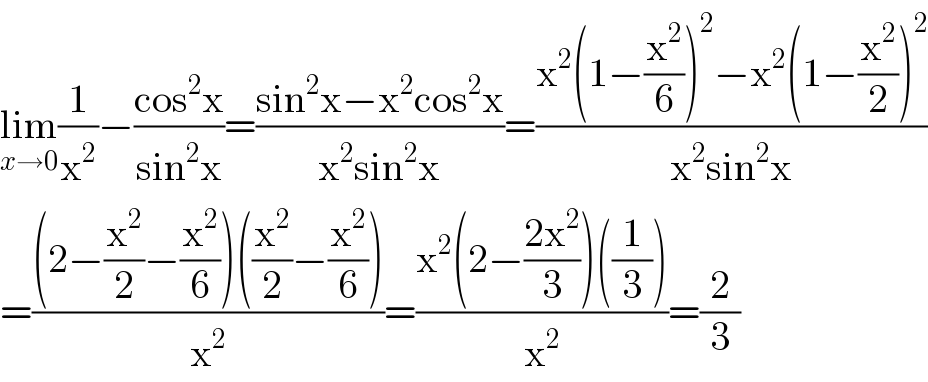
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}=\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{x}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}}=\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}} \\ $$$$=\frac{\left(\mathrm{2}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\right)\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\right)}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{3}}\right)\left(\frac{\mathrm{1}}{\mathrm{3}}\right)}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Sep/20
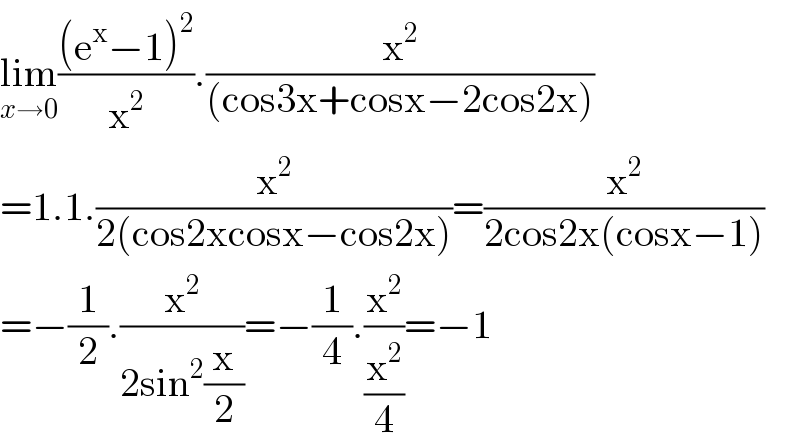
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} }.\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{cos3x}+\mathrm{cosx}−\mathrm{2cos2x}\right)} \\ $$$$=\mathrm{1}.\mathrm{1}.\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{cos2xcosx}−\mathrm{cos2x}\right)}=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2cos2x}\left(\mathrm{cosx}−\mathrm{1}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2sin}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}=−\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{x}^{\mathrm{2}} }{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}}=−\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 28/Sep/20
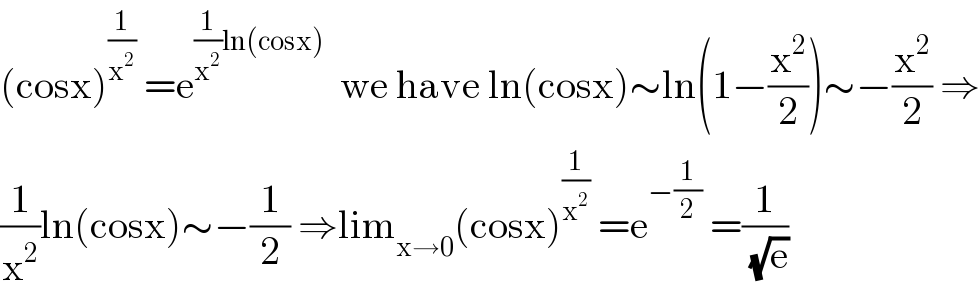
$$\left(\mathrm{cosx}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{cosx}\right)} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{ln}\left(\mathrm{cosx}\right)\sim\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{cosx}\right)\sim−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \left(\mathrm{cosx}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \:=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\sqrt{\mathrm{e}}} \\ $$
Answered by mathmax by abdo last updated on 28/Sep/20
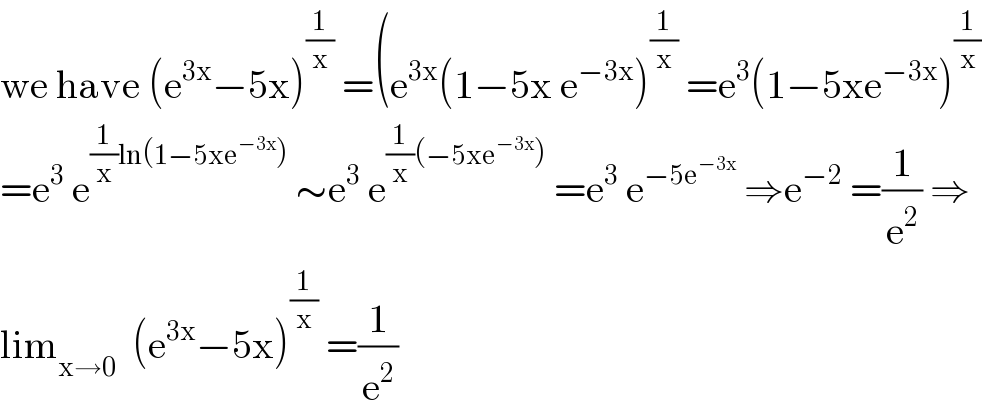
$$\mathrm{we}\:\mathrm{have}\:\left(\mathrm{e}^{\mathrm{3x}} −\mathrm{5x}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\left(\mathrm{e}^{\mathrm{3x}} \left(\mathrm{1}−\mathrm{5x}\:\mathrm{e}^{−\mathrm{3x}} \right)^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\mathrm{e}^{\mathrm{3}} \left(\mathrm{1}−\mathrm{5xe}^{−\mathrm{3x}} \right)^{\frac{\mathrm{1}}{\mathrm{x}}} \right. \\ $$$$=\mathrm{e}^{\mathrm{3}} \:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{1}−\mathrm{5xe}^{−\mathrm{3x}} \right)} \:\sim\mathrm{e}^{\mathrm{3}} \:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}\left(−\mathrm{5xe}^{−\mathrm{3x}} \right)} \:=\mathrm{e}^{\mathrm{3}} \:\mathrm{e}^{−\mathrm{5e}^{−\mathrm{3x}} } \:\Rightarrow\mathrm{e}^{−\mathrm{2}} \:=\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\left(\mathrm{e}^{\mathrm{3x}} −\mathrm{5x}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{2}} } \\ $$
Commented by Dwaipayan Shikari last updated on 28/Sep/20
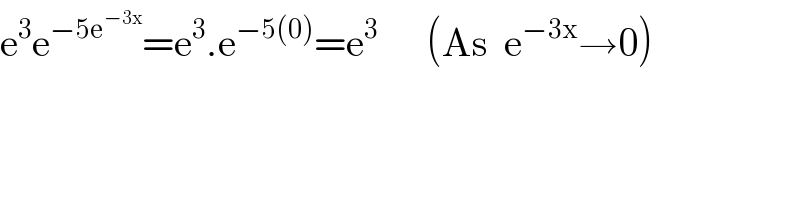
$$\mathrm{e}^{\mathrm{3}} \mathrm{e}^{−\mathrm{5e}^{−\mathrm{3x}} } =\mathrm{e}^{\mathrm{3}} .\mathrm{e}^{−\mathrm{5}\left(\mathrm{0}\right)} =\mathrm{e}^{\mathrm{3}} \:\:\:\:\:\:\left(\mathrm{As}\:\:\mathrm{e}^{−\mathrm{3x}} \rightarrow\mathrm{0}\right) \\ $$
Commented by Bird last updated on 28/Sep/20
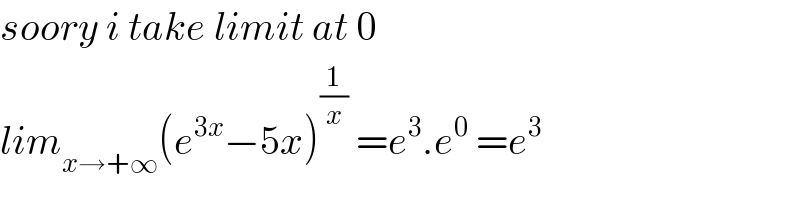
$${soory}\:{i}\:{take}\:{limit}\:{at}\:\mathrm{0} \\ $$$${lim}_{{x}\rightarrow+\infty} \left({e}^{\mathrm{3}{x}} −\mathrm{5}{x}\right)^{\frac{\mathrm{1}}{{x}}} \:={e}^{\mathrm{3}} .{e}^{\mathrm{0}} \:={e}^{\mathrm{3}} \\ $$
Answered by mathmax by abdo last updated on 28/Sep/20
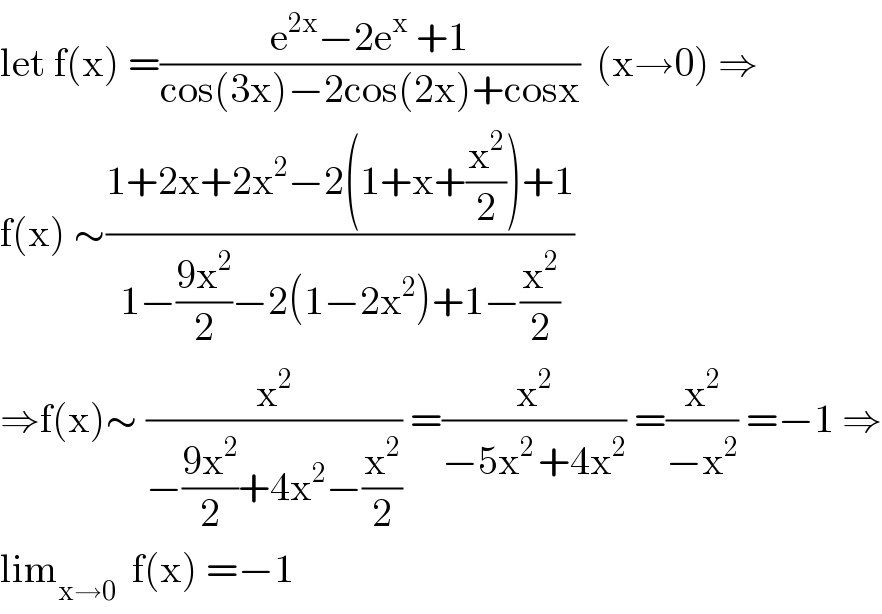
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{e}^{\mathrm{2x}} −\mathrm{2e}^{\mathrm{x}} \:+\mathrm{1}}{\mathrm{cos}\left(\mathrm{3x}\right)−\mathrm{2cos}\left(\mathrm{2x}\right)+\mathrm{cosx}}\:\:\left(\mathrm{x}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:\sim\frac{\mathrm{1}+\mathrm{2x}+\mathrm{2x}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}+\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)+\mathrm{1}}{\mathrm{1}−\frac{\mathrm{9x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\left(\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \right)+\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\sim\:\frac{\mathrm{x}^{\mathrm{2}} }{−\frac{\mathrm{9x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{4x}^{\mathrm{2}} −\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}}\:=\frac{\mathrm{x}^{\mathrm{2}} }{−\mathrm{5x}^{\mathrm{2}\:} +\mathrm{4x}^{\mathrm{2}} }\:=\frac{\mathrm{x}^{\mathrm{2}} }{−\mathrm{x}^{\mathrm{2}} }\:=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{f}\left(\mathrm{x}\right)\:=−\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 28/Sep/20
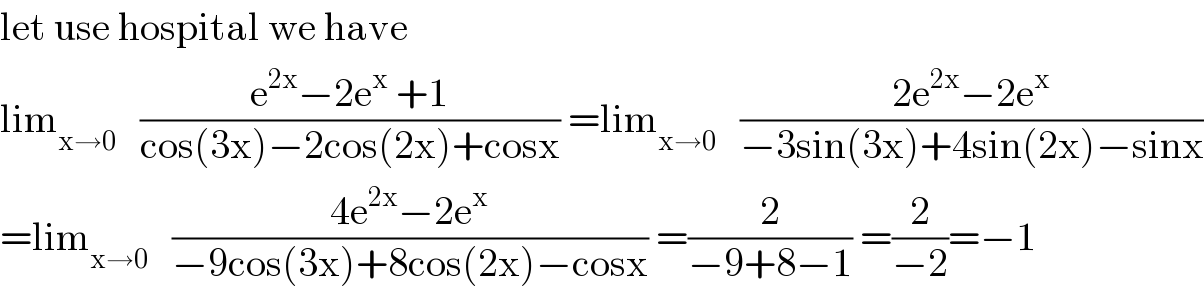
$$\mathrm{let}\:\mathrm{use}\:\mathrm{hospital}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{e}^{\mathrm{2x}} −\mathrm{2e}^{\mathrm{x}} \:+\mathrm{1}}{\mathrm{cos}\left(\mathrm{3x}\right)−\mathrm{2cos}\left(\mathrm{2x}\right)+\mathrm{cosx}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{2e}^{\mathrm{2x}} −\mathrm{2e}^{\mathrm{x}} }{−\mathrm{3sin}\left(\mathrm{3x}\right)+\mathrm{4sin}\left(\mathrm{2x}\right)−\mathrm{sinx}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{4e}^{\mathrm{2x}} −\mathrm{2e}^{\mathrm{x}} }{−\mathrm{9cos}\left(\mathrm{3x}\right)+\mathrm{8cos}\left(\mathrm{2x}\right)−\mathrm{cosx}}\:=\frac{\mathrm{2}}{−\mathrm{9}+\mathrm{8}−\mathrm{1}}\:=\frac{\mathrm{2}}{−\mathrm{2}}=−\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 28/Sep/20
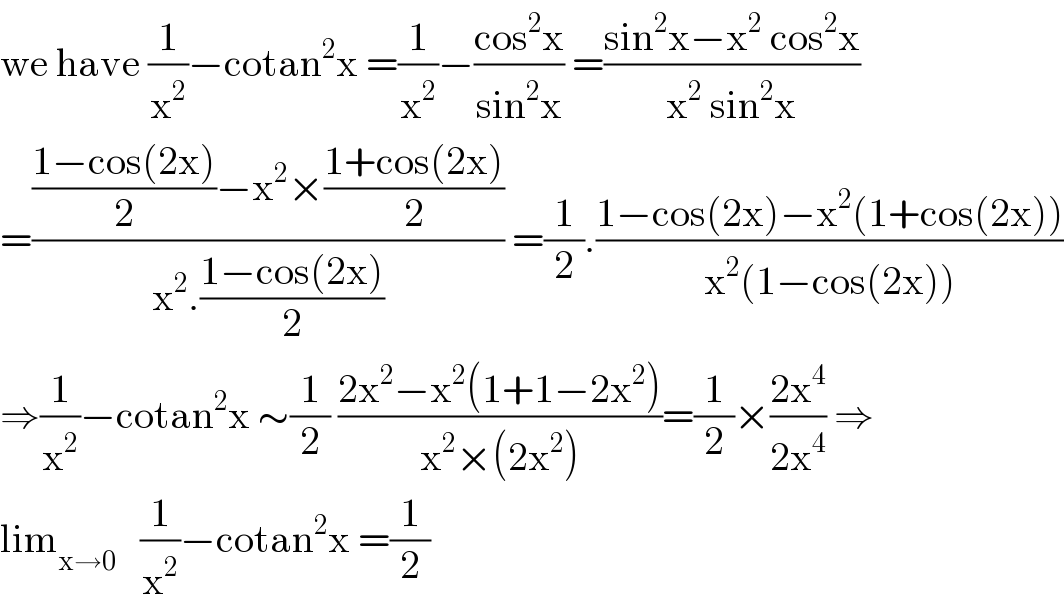
$$\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{cotan}^{\mathrm{2}} \mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\:=\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{x}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \mathrm{x}} \\ $$$$=\frac{\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}−\mathrm{x}^{\mathrm{2}} ×\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} .\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)\right)} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{cotan}^{\mathrm{2}} \mathrm{x}\:\sim\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} ×\left(\mathrm{2x}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2x}^{\mathrm{4}} }{\mathrm{2x}^{\mathrm{4}} }\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{cotan}^{\mathrm{2}} \mathrm{x}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 28/Sep/20

Answered by john santu last updated on 29/Sep/20
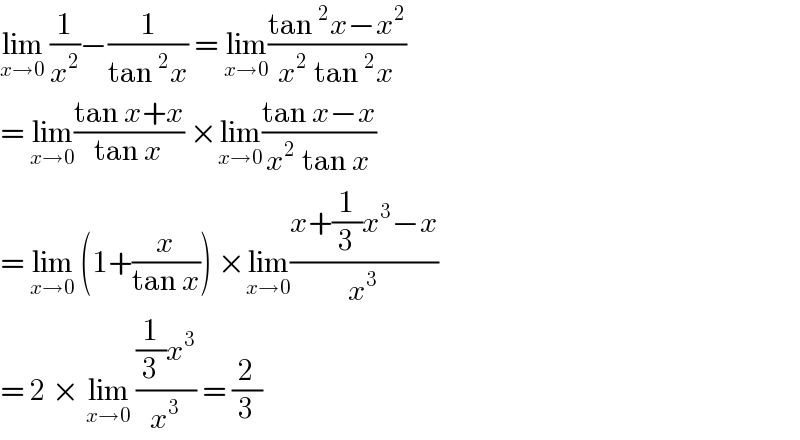
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} {x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:^{\mathrm{2}} {x}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:\mathrm{tan}\:^{\mathrm{2}} {x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:{x}+{x}}{\mathrm{tan}\:{x}}\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:{x}−{x}}{{x}^{\mathrm{2}} \:\mathrm{tan}\:{x}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{{x}}{\mathrm{tan}\:{x}}\right)\:×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}+\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} −{x}}{{x}^{\mathrm{3}} } \\ $$$$=\:\mathrm{2}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
