
Question Number 115743 by bemath last updated on 28/Sep/20
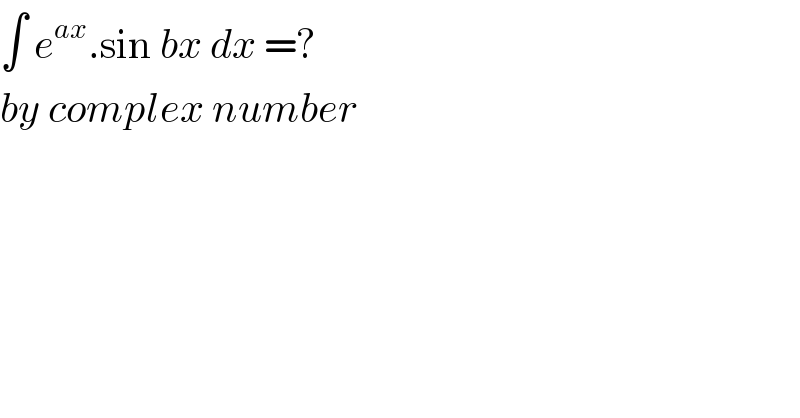
$$\int\:{e}^{{ax}} .\mathrm{sin}\:{bx}\:{dx}\:=? \\ $$$${by}\:{complex}\:{number} \\ $$
Answered by Ar Brandon last updated on 28/Sep/20
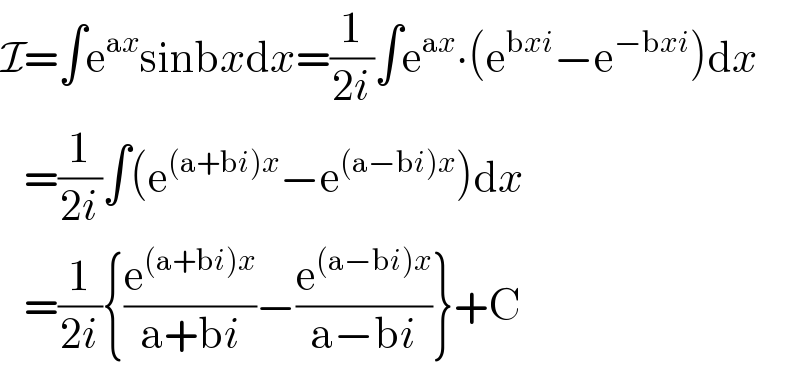
$$\mathcal{I}=\int\mathrm{e}^{\mathrm{a}{x}} \mathrm{sinb}{x}\mathrm{d}{x}=\frac{\mathrm{1}}{\mathrm{2}{i}}\int\mathrm{e}^{\mathrm{a}{x}} \centerdot\left(\mathrm{e}^{\mathrm{b}{xi}} −\mathrm{e}^{−\mathrm{b}{xi}} \right)\mathrm{d}{x} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\int\left(\mathrm{e}^{\left(\mathrm{a}+\mathrm{b}{i}\right){x}} −\mathrm{e}^{\left(\mathrm{a}−\mathrm{b}{i}\right){x}} \right)\mathrm{d}{x} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\frac{\mathrm{e}^{\left(\mathrm{a}+\mathrm{b}{i}\right){x}} }{\mathrm{a}+\mathrm{b}{i}}−\frac{\mathrm{e}^{\left(\mathrm{a}−\mathrm{b}{i}\right){x}} }{\mathrm{a}−\mathrm{b}{i}}\right\}+\mathrm{C} \\ $$
Commented by bemath last updated on 28/Sep/20

$${santuy}\:{bro}.\:{gave}\:{kudos} \\ $$
Answered by Dwaipayan Shikari last updated on 28/Sep/20
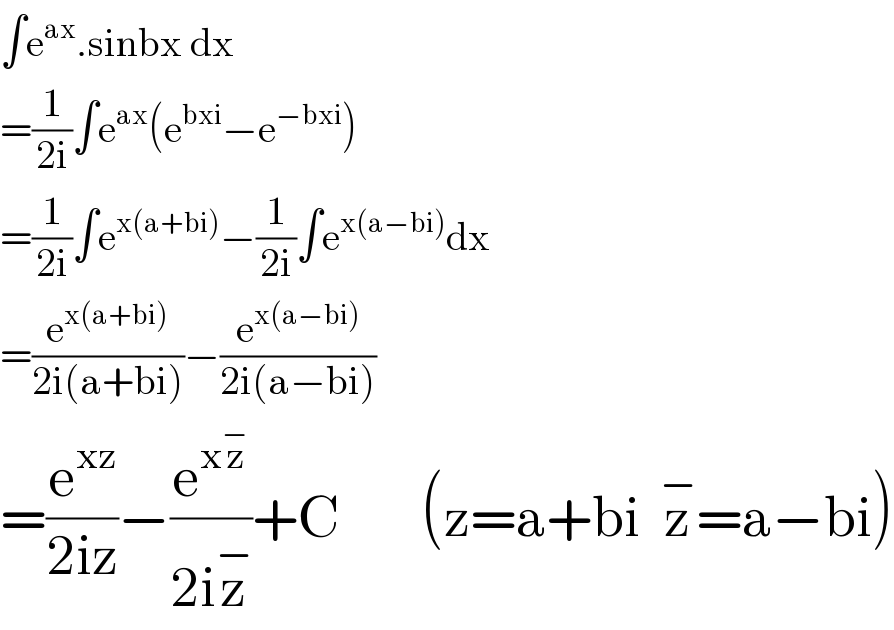
$$\int\mathrm{e}^{\mathrm{ax}} .\mathrm{sinbx}\:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\int\mathrm{e}^{\mathrm{ax}} \left(\mathrm{e}^{\mathrm{bxi}} −\mathrm{e}^{−\mathrm{bxi}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2i}}\int\mathrm{e}^{\mathrm{x}\left(\mathrm{a}+\mathrm{bi}\right)} −\frac{\mathrm{1}}{\mathrm{2i}}\int\mathrm{e}^{\mathrm{x}\left(\mathrm{a}−\mathrm{bi}\right)} \mathrm{dx}\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$=\frac{\mathrm{e}^{\mathrm{x}\left(\mathrm{a}+\mathrm{bi}\right)} }{\mathrm{2i}\left(\mathrm{a}+\mathrm{bi}\right)}−\frac{\mathrm{e}^{\mathrm{x}\left(\mathrm{a}−\mathrm{bi}\right)} }{\mathrm{2i}\left(\mathrm{a}−\mathrm{bi}\right)} \\ $$$$=\frac{\mathrm{e}^{\mathrm{xz}} }{\mathrm{2iz}}−\frac{\mathrm{e}^{\mathrm{x}\overset{−} {\mathrm{z}}} }{\mathrm{2i}\overset{−} {\mathrm{z}}}+\mathrm{C}\:\:\:\:\:\:\:\:\left(\mathrm{z}=\mathrm{a}+\mathrm{bi}\:\:\overset{−} {\mathrm{z}}=\mathrm{a}−\mathrm{bi}\right) \\ $$
Answered by mathmax by abdo last updated on 28/Sep/20
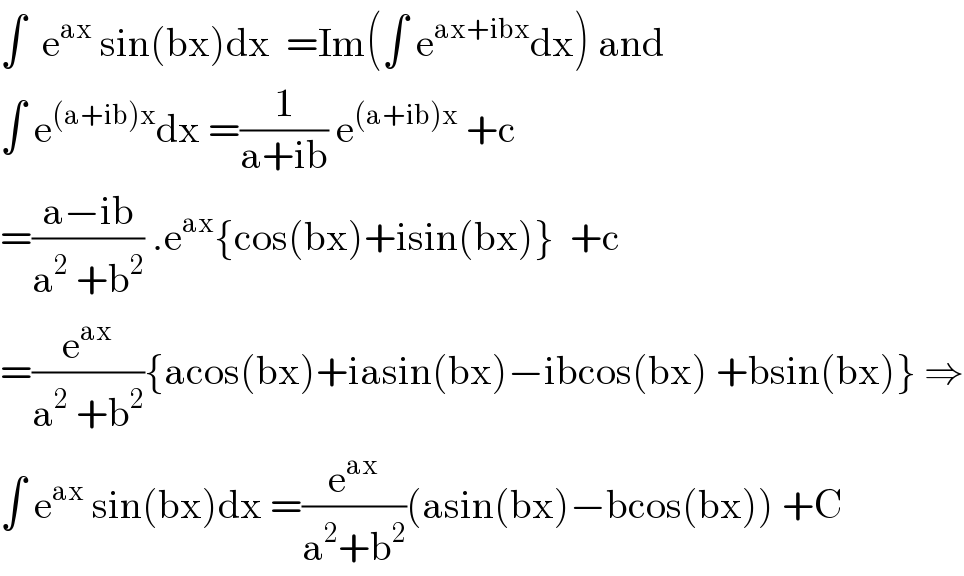
$$\int\:\:\mathrm{e}^{\mathrm{ax}} \:\mathrm{sin}\left(\mathrm{bx}\right)\mathrm{dx}\:\:=\mathrm{Im}\left(\int\:\mathrm{e}^{\mathrm{ax}+\mathrm{ibx}} \mathrm{dx}\right)\:\mathrm{and} \\ $$$$\int\:\mathrm{e}^{\left(\mathrm{a}+\mathrm{ib}\right)\mathrm{x}} \mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{a}+\mathrm{ib}}\:\mathrm{e}^{\left(\mathrm{a}+\mathrm{ib}\right)\mathrm{x}} \:+\mathrm{c} \\ $$$$=\frac{\mathrm{a}−\mathrm{ib}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }\:.\mathrm{e}^{\mathrm{ax}} \left\{\mathrm{cos}\left(\mathrm{bx}\right)+\mathrm{isin}\left(\mathrm{bx}\right)\right\}\:\:+\mathrm{c} \\ $$$$=\frac{\mathrm{e}^{\mathrm{ax}} }{\mathrm{a}^{\mathrm{2}} \:+\mathrm{b}^{\mathrm{2}} }\left\{\mathrm{acos}\left(\mathrm{bx}\right)+\mathrm{iasin}\left(\mathrm{bx}\right)−\mathrm{ibcos}\left(\mathrm{bx}\right)\:+\mathrm{bsin}\left(\mathrm{bx}\right)\right\}\:\Rightarrow \\ $$$$\int\:\mathrm{e}^{\mathrm{ax}} \:\mathrm{sin}\left(\mathrm{bx}\right)\mathrm{dx}\:=\frac{\mathrm{e}^{\mathrm{ax}} }{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\left(\mathrm{asin}\left(\mathrm{bx}\right)−\mathrm{bcos}\left(\mathrm{bx}\right)\right)\:+\mathrm{C} \\ $$
