
Question Number 115732 by gab last updated on 28/Sep/20

Commented by Dwaipayan Shikari last updated on 28/Sep/20
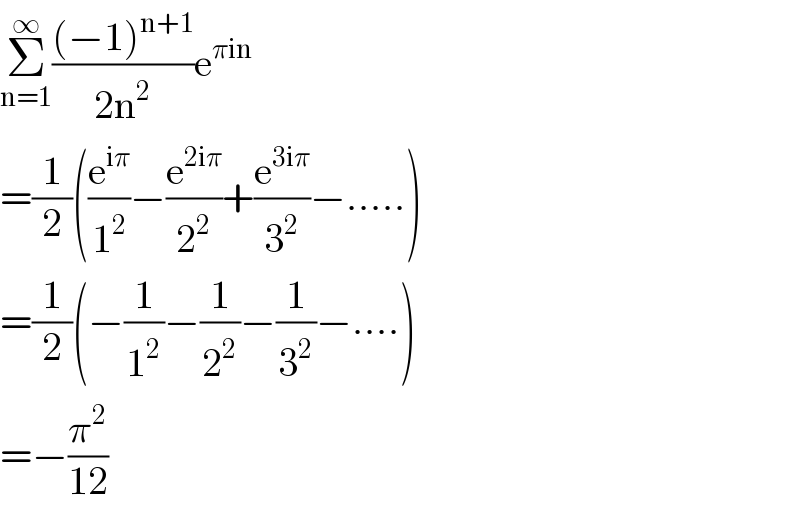
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{2n}^{\mathrm{2}} }\mathrm{e}^{\pi\mathrm{in}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{e}^{\mathrm{i}\pi} }{\mathrm{1}^{\mathrm{2}} }−\frac{\mathrm{e}^{\mathrm{2i}\pi} }{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{e}^{\mathrm{3i}\pi} }{\mathrm{3}^{\mathrm{2}} }−.....\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }−....\right) \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
