
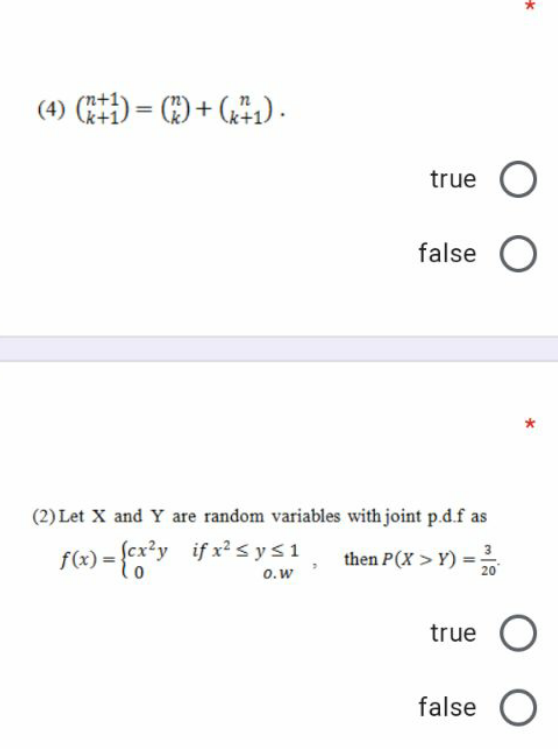
Question Number 115683 by mohammad17 last updated on 27/Sep/20
Answered by Dwaipayan Shikari last updated on 27/Sep/20
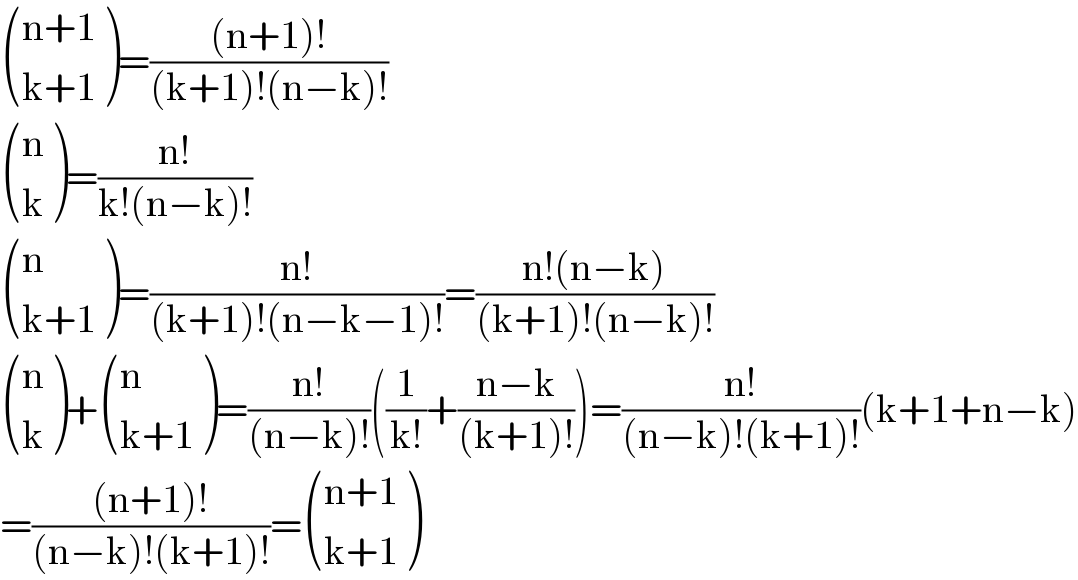
$$\begin{pmatrix}{\mathrm{n}+\mathrm{1}}\\{\mathrm{k}+\mathrm{1}}\end{pmatrix}=\frac{\left(\mathrm{n}+\mathrm{1}\right)!}{\left(\mathrm{k}+\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{k}\right)!} \\ $$$$\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}=\frac{\mathrm{n}!}{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!} \\ $$$$\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}+\mathrm{1}}\end{pmatrix}=\frac{\mathrm{n}!}{\left(\mathrm{k}+\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{k}−\mathrm{1}\right)!}=\frac{\mathrm{n}!\left(\mathrm{n}−\mathrm{k}\right)}{\left(\mathrm{k}+\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{k}\right)!} \\ $$$$\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}+\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}+\mathrm{1}}\end{pmatrix}=\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{k}\right)!}\left(\frac{\mathrm{1}}{\mathrm{k}!}+\frac{\mathrm{n}−\mathrm{k}}{\left(\mathrm{k}+\mathrm{1}\right)!}\right)=\frac{\mathrm{n}!}{\left(\mathrm{n}−\mathrm{k}\right)!\left(\mathrm{k}+\mathrm{1}\right)!}\left(\mathrm{k}+\mathrm{1}+\mathrm{n}−\mathrm{k}\right) \\ $$$$=\frac{\left(\mathrm{n}+\mathrm{1}\right)!}{\left(\mathrm{n}−\mathrm{k}\right)!\left(\mathrm{k}+\mathrm{1}\right)!}=\begin{pmatrix}{\mathrm{n}+\mathrm{1}}\\{\mathrm{k}+\mathrm{1}}\end{pmatrix} \\ $$
