Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 115656 by bobhans last updated on 27/Sep/20

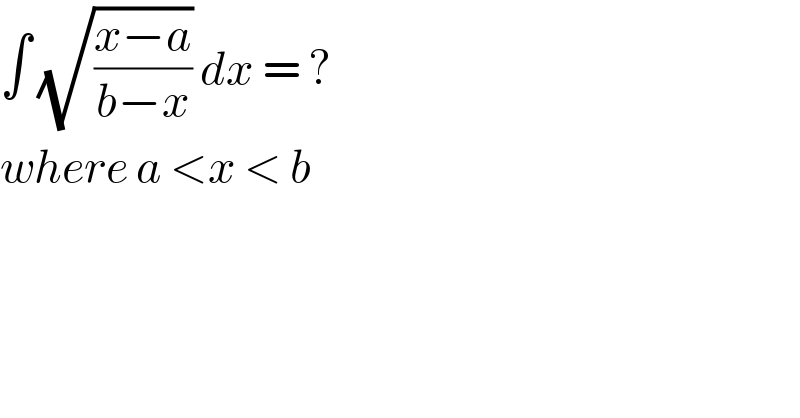
∫ (√((x−a)/(b−x))) dx = ? where a <x < b

$$\int\:\sqrt{\frac{{x}−{a}}{{b}−{x}}}\:{dx}\:=\:? \\ $$ $${where}\:{a}\:<{x}\:<\:{b} \\ $$

Commented bybemath last updated on 27/Sep/20

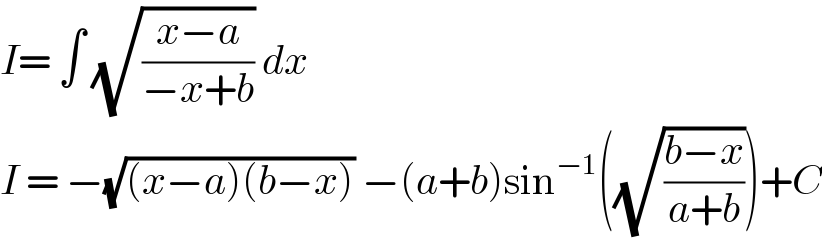
I= ∫ (√((x−a)/(−x+b))) dx I = −(√((x−a)(b−x))) −(a+b)sin^(−1) ((√((b−x)/(a+b))))+C

$${I}=\:\int\:\sqrt{\frac{{x}−{a}}{−{x}+{b}}}\:{dx}\: \\ $$ $${I}\:=\:−\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}\:−\left({a}+{b}\right)\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\frac{{b}−{x}}{{a}+{b}}}\right)+{C} \\ $$

Answered by bobhans last updated on 27/Sep/20

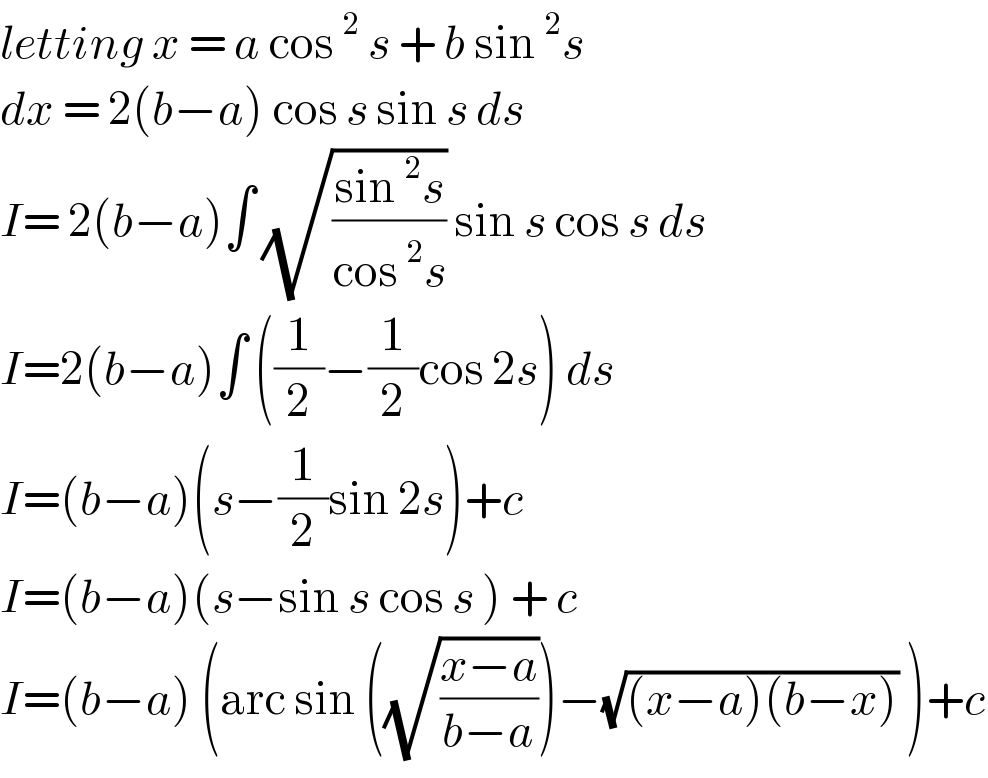
letting x = a cos^2 s + b sin^2 s dx = 2(b−a) cos s sin s ds I= 2(b−a)∫ (√((sin^2 s)/(cos^2 s))) sin s cos s ds I=2(b−a)∫ ((1/2)−(1/2)cos 2s) ds I=(b−a)(s−(1/2)sin 2s)+c I=(b−a)(s−sin s cos s ) + c I=(b−a) (arc sin ((√((x−a)/(b−a))))−(√((x−a)(b−x))) )+c

$${letting}\:{x}\:=\:{a}\:\mathrm{cos}\:^{\mathrm{2}} \:{s}\:+\:{b}\:\mathrm{sin}\:^{\mathrm{2}} {s} \\ $$ $${dx}\:=\:\mathrm{2}\left({b}−{a}\right)\:\mathrm{cos}\:{s}\:\mathrm{sin}\:{s}\:{ds} \\ $$ $${I}=\:\mathrm{2}\left({b}−{a}\right)\int\:\sqrt{\frac{\mathrm{sin}\:^{\mathrm{2}} {s}}{\mathrm{cos}\:^{\mathrm{2}} {s}}}\:\mathrm{sin}\:{s}\:\mathrm{cos}\:{s}\:{ds} \\ $$ $${I}=\mathrm{2}\left({b}−{a}\right)\int\:\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{s}\right)\:{ds} \\ $$ $${I}=\left({b}−{a}\right)\left({s}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{s}\right)+{c} \\ $$ $${I}=\left({b}−{a}\right)\left({s}−\mathrm{sin}\:{s}\:\mathrm{cos}\:{s}\:\right)\:+\:{c} \\ $$ $${I}=\left({b}−{a}\right)\:\left(\mathrm{arc}\:\mathrm{sin}\:\left(\sqrt{\frac{{x}−{a}}{{b}−{a}}}\right)−\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}\:\right)+{c} \\ $$

Answered by TANMAY PANACEA last updated on 27/Sep/20

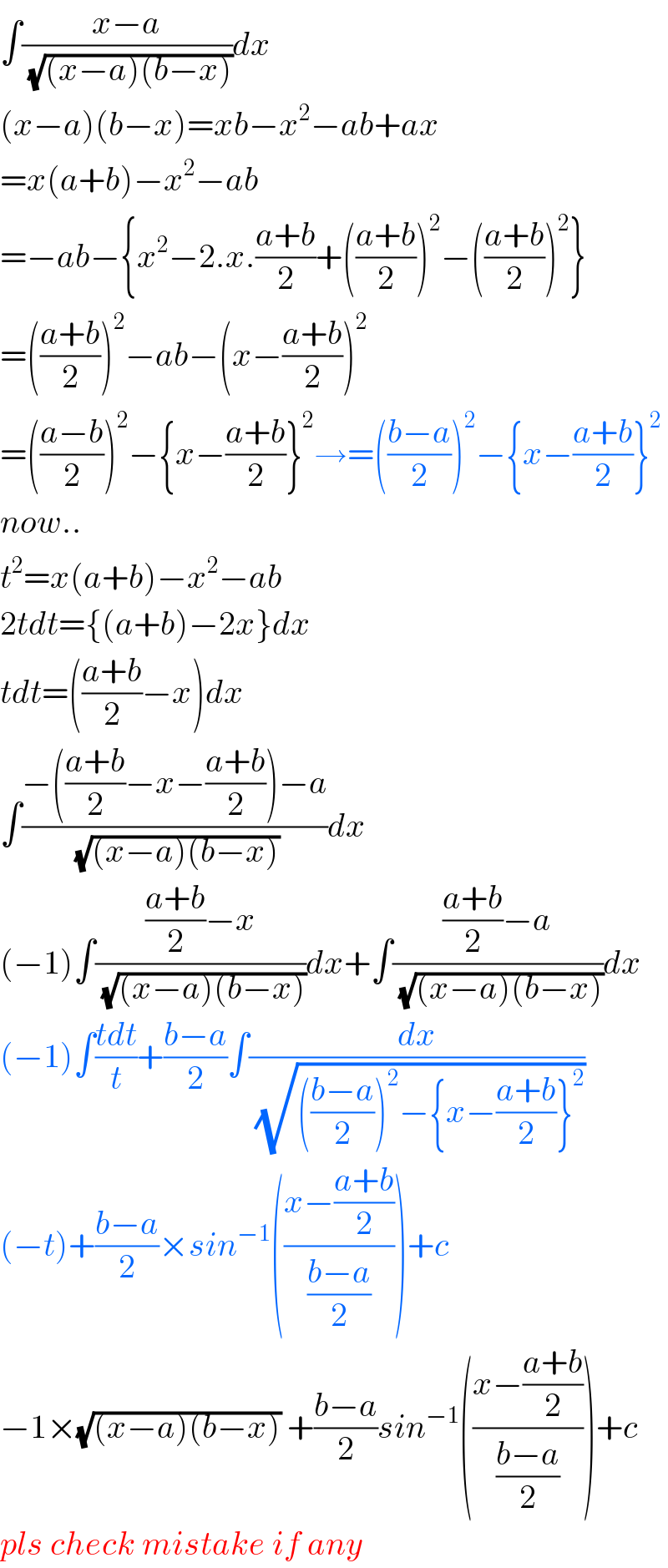
∫((x−a)/( (√((x−a)(b−x)))))dx (x−a)(b−x)=xb−x^2 −ab+ax =x(a+b)−x^2 −ab =−ab−{x^2 −2.x.((a+b)/2)+(((a+b)/2))^2 −(((a+b)/2))^2 } =(((a+b)/2))^2 −ab−(x−((a+b)/2))^2 =(((a−b)/2))^2 −{x−((a+b)/2)}^2 →=(((b−a)/2))^2 −{x−((a+b)/2)}^2 now.. t^2 =x(a+b)−x^2 −ab 2tdt={(a+b)−2x}dx tdt=(((a+b)/2)−x)dx ∫((−(((a+b)/2)−x−((a+b)/2))−a)/( (√((x−a)(b−x)))))dx (−1)∫((((a+b)/2)−x)/( (√((x−a)(b−x)))))dx+∫((((a+b)/2)−a)/( (√((x−a)(b−x)))))dx (−1)∫((tdt)/t)+((b−a)/2)∫(dx/( (√((((b−a)/2))^2 −{x−((a+b)/2)}^2 )))) (−t)+((b−a)/2)×sin^(−1) (((x−((a+b)/2))/((b−a)/2)))+c −1×(√((x−a)(b−x))) +((b−a)/2)sin^(−1) (((x−((a+b)/2))/((b−a)/2)))+c pls check mistake if any

$$\int\frac{{x}−{a}}{\:\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}}{dx} \\ $$ $$\left({x}−{a}\right)\left({b}−{x}\right)={xb}−{x}^{\mathrm{2}} −{ab}+{ax} \\ $$ $$={x}\left({a}+{b}\right)−{x}^{\mathrm{2}} −{ab} \\ $$ $$=−{ab}−\left\{{x}^{\mathrm{2}} −\mathrm{2}.{x}.\frac{{a}+{b}}{\mathrm{2}}+\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} \right\} \\ $$ $$=\left(\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} −{ab}−\left({x}−\frac{{a}+{b}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$ $$=\left(\frac{{a}−{b}}{\mathrm{2}}\right)^{\mathrm{2}} −\left\{{x}−\frac{{a}+{b}}{\mathrm{2}}\right\}^{\mathrm{2}} \rightarrow=\left(\frac{{b}−{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\left\{{x}−\frac{{a}+{b}}{\mathrm{2}}\right\}^{\mathrm{2}} \\ $$ $${now}.. \\ $$ $${t}^{\mathrm{2}} ={x}\left({a}+{b}\right)−{x}^{\mathrm{2}} −{ab} \\ $$ $$\mathrm{2}{tdt}=\left\{\left({a}+{b}\right)−\mathrm{2}{x}\right\}{dx} \\ $$ $${tdt}=\left(\frac{{a}+{b}}{\mathrm{2}}−{x}\right){dx} \\ $$ $$\int\frac{−\left(\frac{{a}+{b}}{\mathrm{2}}−{x}−\frac{{a}+{b}}{\mathrm{2}}\right)−{a}}{\:\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}}{dx} \\ $$ $$\left(−\mathrm{1}\right)\int\frac{\frac{{a}+{b}}{\mathrm{2}}−{x}}{\:\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}}{dx}+\int\frac{\frac{{a}+{b}}{\mathrm{2}}−{a}}{\:\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}}{dx} \\ $$ $$\left(−\mathrm{1}\right)\int\frac{{tdt}}{{t}}+\frac{{b}−{a}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{\left(\frac{{b}−{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\left\{{x}−\frac{{a}+{b}}{\mathrm{2}}\right\}^{\mathrm{2}} }} \\ $$ $$\left(−{t}\right)+\frac{{b}−{a}}{\mathrm{2}}×{sin}^{−\mathrm{1}} \left(\frac{{x}−\frac{{a}+{b}}{\mathrm{2}}}{\frac{{b}−{a}}{\mathrm{2}}}\right)+{c} \\ $$ $$−\mathrm{1}×\sqrt{\left({x}−{a}\right)\left({b}−{x}\right)}\:+\frac{{b}−{a}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}−\frac{{a}+{b}}{\mathrm{2}}}{\frac{{b}−{a}}{\mathrm{2}}}\right)+{c} \\ $$ $${pls}\:{check}\:{mistake}\:{if}\:{any} \\ $$

Answered by Bird last updated on 27/Sep/20

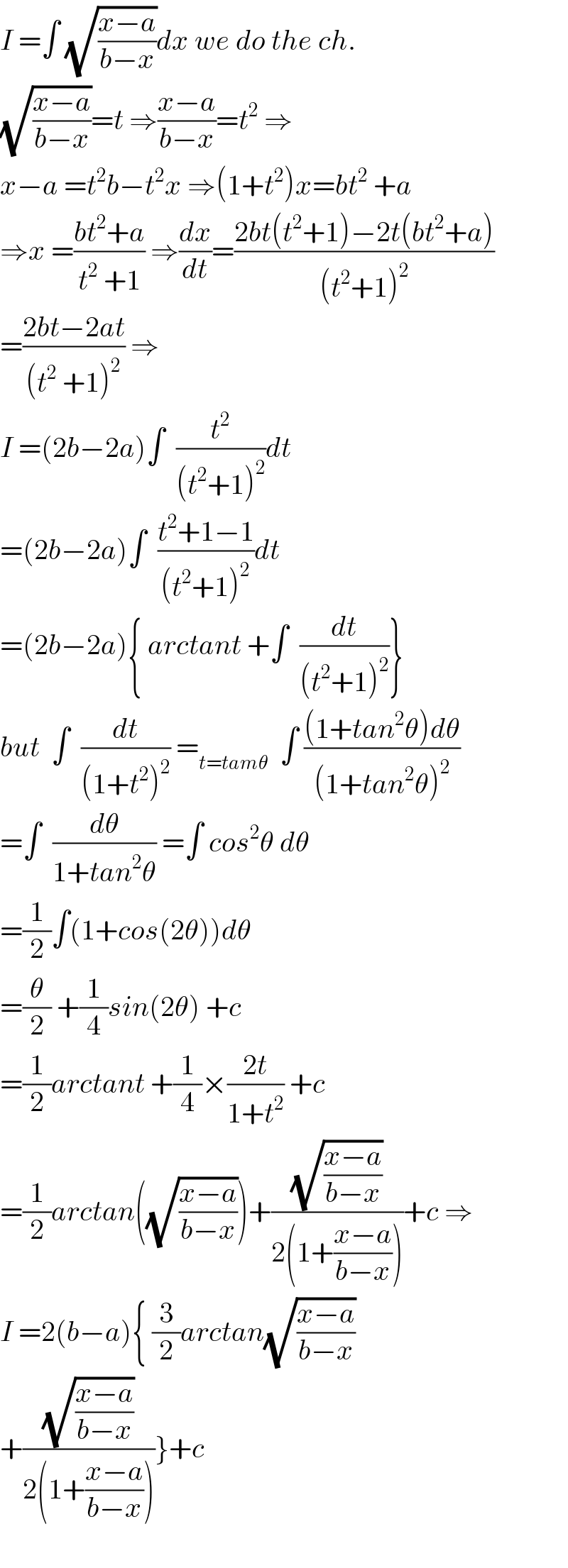
I =∫ (√((x−a)/(b−x)))dx we do the ch. (√((x−a)/(b−x)))=t ⇒((x−a)/(b−x))=t^2 ⇒ x−a =t^2 b−t^2 x ⇒(1+t^2 )x=bt^2 +a ⇒x =((bt^2 +a)/(t^2 +1)) ⇒(dx/dt)=((2bt(t^2 +1)−2t(bt^2 +a))/((t^2 +1)^2 )) =((2bt−2at)/((t^2 +1)^2 )) ⇒ I =(2b−2a)∫ (t^2 /((t^2 +1)^2 ))dt =(2b−2a)∫ ((t^2 +1−1)/((t^2 +1)^2 ))dt =(2b−2a){ arctant +∫ (dt/((t^2 +1)^2 ))} but ∫ (dt/((1+t^2 )^2 )) =_(t=tamθ) ∫ (((1+tan^2 θ)dθ)/((1+tan^2 θ)^2 )) =∫ (dθ/(1+tan^2 θ)) =∫ cos^2 θ dθ =(1/2)∫(1+cos(2θ))dθ =(θ/2) +(1/4)sin(2θ) +c =(1/2)arctant +(1/4)×((2t)/(1+t^2 )) +c =(1/2)arctan((√((x−a)/(b−x))))+((√((x−a)/(b−x)))/(2(1+((x−a)/(b−x)))))+c ⇒ I =2(b−a){ (3/2)arctan(√((x−a)/(b−x))) +((√((x−a)/(b−x)))/(2(1+((x−a)/(b−x)))))}+c

$${I}\:=\int\:\sqrt{\frac{{x}−{a}}{{b}−{x}}}{dx}\:{we}\:{do}\:{the}\:{ch}. \\ $$ $$\sqrt{\frac{{x}−{a}}{{b}−{x}}}={t}\:\Rightarrow\frac{{x}−{a}}{{b}−{x}}={t}^{\mathrm{2}} \:\Rightarrow \\ $$ $${x}−{a}\:={t}^{\mathrm{2}} {b}−{t}^{\mathrm{2}} {x}\:\Rightarrow\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}={bt}^{\mathrm{2}} \:+{a} \\ $$ $$\Rightarrow{x}\:=\frac{{bt}^{\mathrm{2}} +{a}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\frac{{dx}}{{dt}}=\frac{\mathrm{2}{bt}\left({t}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2}{t}\left({bt}^{\mathrm{2}} +{a}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$ $$=\frac{\mathrm{2}{bt}−\mathrm{2}{at}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$ $${I}\:=\left(\mathrm{2}{b}−\mathrm{2}{a}\right)\int\:\:\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$ $$=\left(\mathrm{2}{b}−\mathrm{2}{a}\right)\int\:\:\frac{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$ $$=\left(\mathrm{2}{b}−\mathrm{2}{a}\right)\left\{\:{arctant}\:+\int\:\:\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right\} \\ $$ $${but}\:\:\int\:\:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=_{{t}={tam}\theta} \:\:\int\:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} } \\ $$ $$=\int\:\:\frac{{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:=\int\:{cos}^{\mathrm{2}} \theta\:{d}\theta \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right){d}\theta \\ $$ $$=\frac{\theta}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}\theta\right)\:+{c} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}{arctant}\:+\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+{c} \\ $$ $$=\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\sqrt{\frac{{x}−{a}}{{b}−{x}}}\right)+\frac{\sqrt{\frac{{x}−{a}}{{b}−{x}}}}{\mathrm{2}\left(\mathrm{1}+\frac{{x}−{a}}{{b}−{x}}\right)}+{c}\:\Rightarrow \\ $$ $${I}\:=\mathrm{2}\left({b}−{a}\right)\left\{\:\frac{\mathrm{3}}{\mathrm{2}}{arctan}\sqrt{\frac{{x}−{a}}{{b}−{x}}}\right. \\ $$ $$\left.+\frac{\sqrt{\frac{{x}−{a}}{{b}−{x}}}}{\mathrm{2}\left(\mathrm{1}+\frac{{x}−{a}}{{b}−{x}}\right)}\right\}+{c} \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com