
Question Number 11563 by Nayon last updated on 28/Mar/17
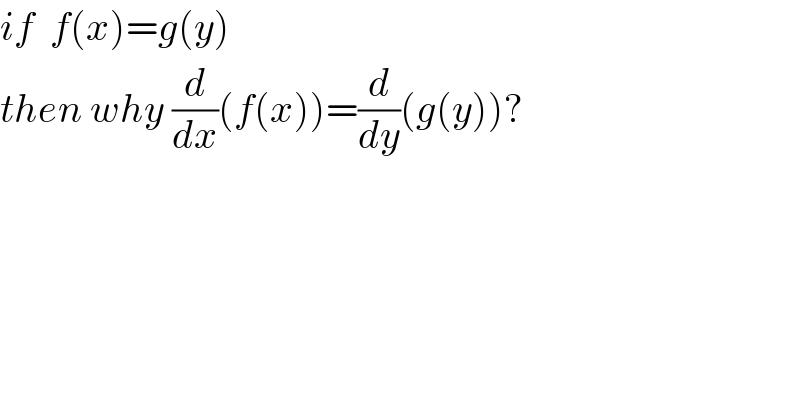
$${if}\:\:{f}\left({x}\right)={g}\left({y}\right) \\ $$$${then}\:{why}\:\frac{{d}}{{dx}}\left({f}\left({x}\right)\right)=\frac{{d}}{{dy}}\left({g}\left({y}\right)\right)? \\ $$
Commented by mrW1 last updated on 28/Mar/17
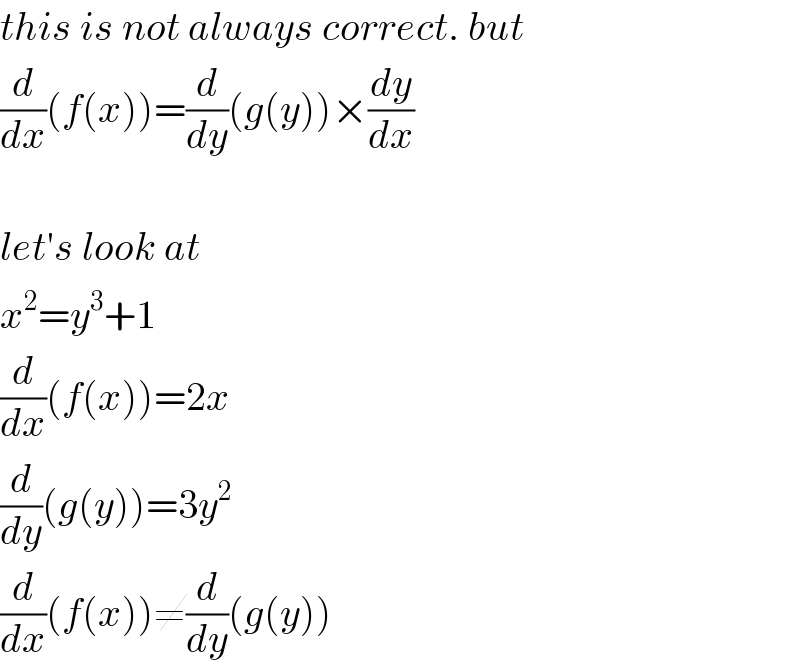
$${this}\:{is}\:{not}\:{always}\:{correct}.\:{but} \\ $$$$\frac{{d}}{{dx}}\left({f}\left({x}\right)\right)=\frac{{d}}{{dy}}\left({g}\left({y}\right)\right)×\frac{{dy}}{{dx}} \\ $$$$ \\ $$$${let}'{s}\:{look}\:{at} \\ $$$${x}^{\mathrm{2}} ={y}^{\mathrm{3}} +\mathrm{1} \\ $$$$\frac{{d}}{{dx}}\left({f}\left({x}\right)\right)=\mathrm{2}{x} \\ $$$$\frac{{d}}{{dy}}\left({g}\left({y}\right)\right)=\mathrm{3}{y}^{\mathrm{2}} \\ $$$$\frac{{d}}{{dx}}\left({f}\left({x}\right)\right)\neq\frac{{d}}{{dy}}\left({g}\left({y}\right)\right) \\ $$
Commented by Nayon last updated on 28/Mar/17
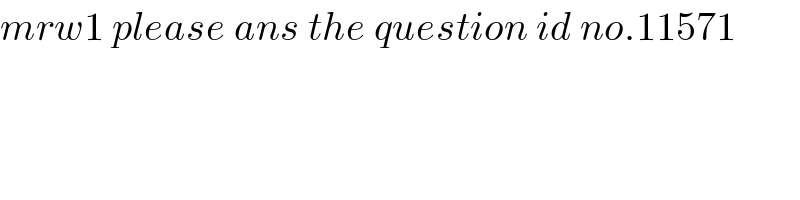
$${mrw}\mathrm{1}\:{please}\:{ans}\:{the}\:{question}\:{id}\:{no}.\mathrm{11571} \\ $$
Answered by sma3l2996 last updated on 28/Mar/17
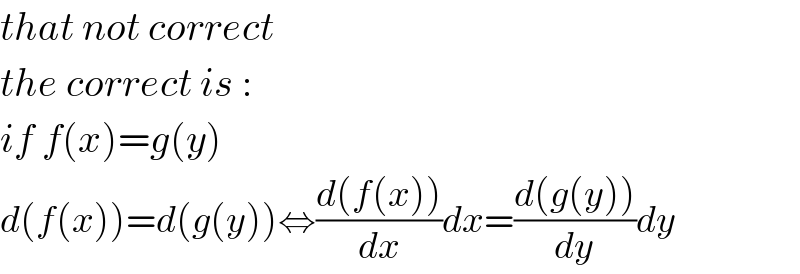
$${that}\:{not}\:{correct} \\ $$$${the}\:{correct}\:{is}\:: \\ $$$${if}\:{f}\left({x}\right)={g}\left({y}\right) \\ $$$${d}\left({f}\left({x}\right)\right)={d}\left({g}\left({y}\right)\right)\Leftrightarrow\frac{{d}\left({f}\left({x}\right)\right)}{{dx}}{dx}=\frac{{d}\left({g}\left({y}\right)\right)}{{dy}}{dy} \\ $$
