
Question Number 115555 by ZiYangLee last updated on 26/Sep/20
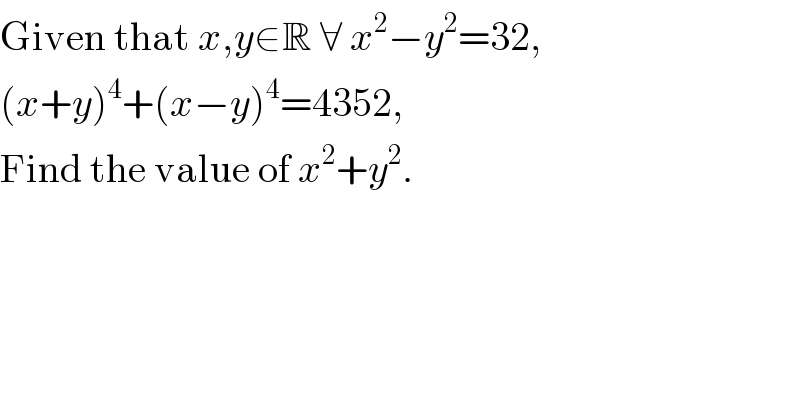
$$\mathrm{Given}\:\mathrm{that}\:{x},{y}\in\mathbb{R}\:\forall\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{32}, \\ $$$$\left({x}+{y}\right)^{\mathrm{4}} +\left({x}−{y}\right)^{\mathrm{4}} =\mathrm{4352},\: \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} . \\ $$
Commented by Rasheed.Sindhi last updated on 27/Sep/20
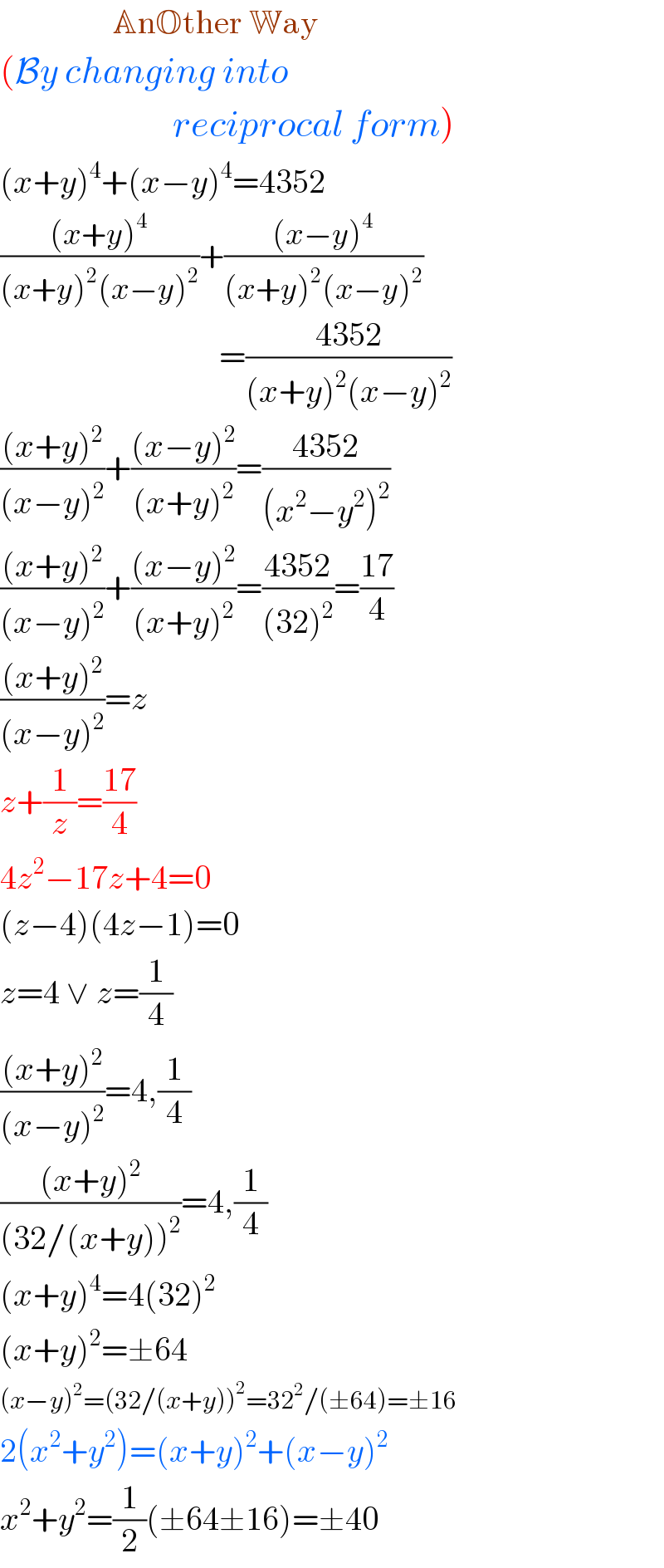
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathbb{A}\mathrm{n}\mathbb{O}\mathrm{ther}\:\mathbb{W}\mathrm{ay} \\ $$$$\left(\mathcal{B}{y}\:{changing}\:{into}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{reciprocal}\:{form}\right) \\ $$$$\left({x}+{y}\right)^{\mathrm{4}} +\left({x}−{y}\right)^{\mathrm{4}} =\mathrm{4352} \\ $$$$\frac{\left({x}+{y}\right)^{\mathrm{4}} }{\left({x}+{y}\right)^{\mathrm{2}} \left({x}−{y}\right)^{\mathrm{2}} }+\frac{\left({x}−{y}\right)^{\mathrm{4}} }{\left({x}+{y}\right)^{\mathrm{2}} \left({x}−{y}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{4352}}{\left({x}+{y}\right)^{\mathrm{2}} \left({x}−{y}\right)^{\mathrm{2}} } \\ $$$$\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\left({x}−{y}\right)^{\mathrm{2}} }+\frac{\left({x}−{y}\right)^{\mathrm{2}} }{\left({x}+{y}\right)^{\mathrm{2}} }=\frac{\mathrm{4352}}{\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\left({x}−{y}\right)^{\mathrm{2}} }+\frac{\left({x}−{y}\right)^{\mathrm{2}} }{\left({x}+{y}\right)^{\mathrm{2}} }=\frac{\mathrm{4352}}{\left(\mathrm{32}\right)^{\mathrm{2}} }=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$$\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\left({x}−{y}\right)^{\mathrm{2}} }={z}\: \\ $$$${z}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{17}}{\mathrm{4}} \\ $$$$\mathrm{4}{z}^{\mathrm{2}} −\mathrm{17}{z}+\mathrm{4}=\mathrm{0} \\ $$$$\left({z}−\mathrm{4}\right)\left(\mathrm{4}{z}−\mathrm{1}\right)=\mathrm{0} \\ $$$${z}=\mathrm{4}\:\vee\:{z}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\left({x}−{y}\right)^{\mathrm{2}} }=\mathrm{4},\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\left(\mathrm{32}/\left({x}+{y}\right)\right)^{\mathrm{2}} }=\mathrm{4},\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left({x}+{y}\right)^{\mathrm{4}} =\mathrm{4}\left(\mathrm{32}\right)^{\mathrm{2}} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} =\pm\mathrm{64} \\ $$$$\left({x}−{y}\right)^{\mathrm{2}} =\left(\mathrm{32}/\left({x}+{y}\right)\right)^{\mathrm{2}} =\mathrm{32}^{\mathrm{2}} /\left(\pm\mathrm{64}\right)=\pm\mathrm{16} \\ $$$$\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\left({x}+{y}\right)^{\mathrm{2}} +\left({x}−{y}\right)^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\pm\mathrm{64}\pm\mathrm{16}\right)=\pm\mathrm{40} \\ $$
Answered by mr W last updated on 26/Sep/20
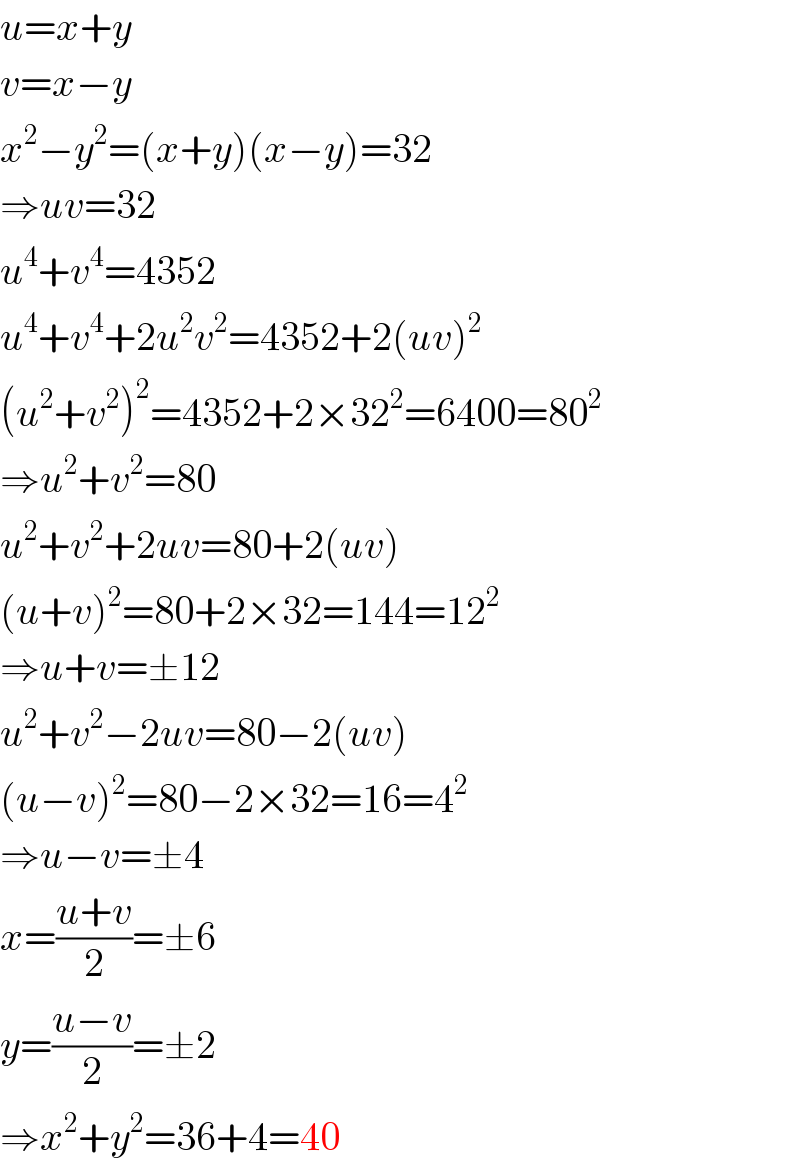
$${u}={x}+{y} \\ $$$${v}={x}−{y} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\left({x}+{y}\right)\left({x}−{y}\right)=\mathrm{32} \\ $$$$\Rightarrow{uv}=\mathrm{32} \\ $$$${u}^{\mathrm{4}} +{v}^{\mathrm{4}} =\mathrm{4352} \\ $$$${u}^{\mathrm{4}} +{v}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} {v}^{\mathrm{2}} =\mathrm{4352}+\mathrm{2}\left({uv}\right)^{\mathrm{2}} \\ $$$$\left({u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4352}+\mathrm{2}×\mathrm{32}^{\mathrm{2}} =\mathrm{6400}=\mathrm{80}^{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} +{v}^{\mathrm{2}} =\mathrm{80} \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} +\mathrm{2}{uv}=\mathrm{80}+\mathrm{2}\left({uv}\right) \\ $$$$\left({u}+{v}\right)^{\mathrm{2}} =\mathrm{80}+\mathrm{2}×\mathrm{32}=\mathrm{144}=\mathrm{12}^{\mathrm{2}} \\ $$$$\Rightarrow{u}+{v}=\pm\mathrm{12} \\ $$$${u}^{\mathrm{2}} +{v}^{\mathrm{2}} −\mathrm{2}{uv}=\mathrm{80}−\mathrm{2}\left({uv}\right) \\ $$$$\left({u}−{v}\right)^{\mathrm{2}} =\mathrm{80}−\mathrm{2}×\mathrm{32}=\mathrm{16}=\mathrm{4}^{\mathrm{2}} \\ $$$$\Rightarrow{u}−{v}=\pm\mathrm{4} \\ $$$${x}=\frac{{u}+{v}}{\mathrm{2}}=\pm\mathrm{6} \\ $$$${y}=\frac{{u}−{v}}{\mathrm{2}}=\pm\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{36}+\mathrm{4}=\mathrm{40} \\ $$
Commented by ZiYangLee last updated on 26/Sep/20
$$\mathrm{Thanks}\:\mathrm{very}\:\mathrm{much}.. \\ $$
Answered by ruwedkabeh last updated on 26/Sep/20
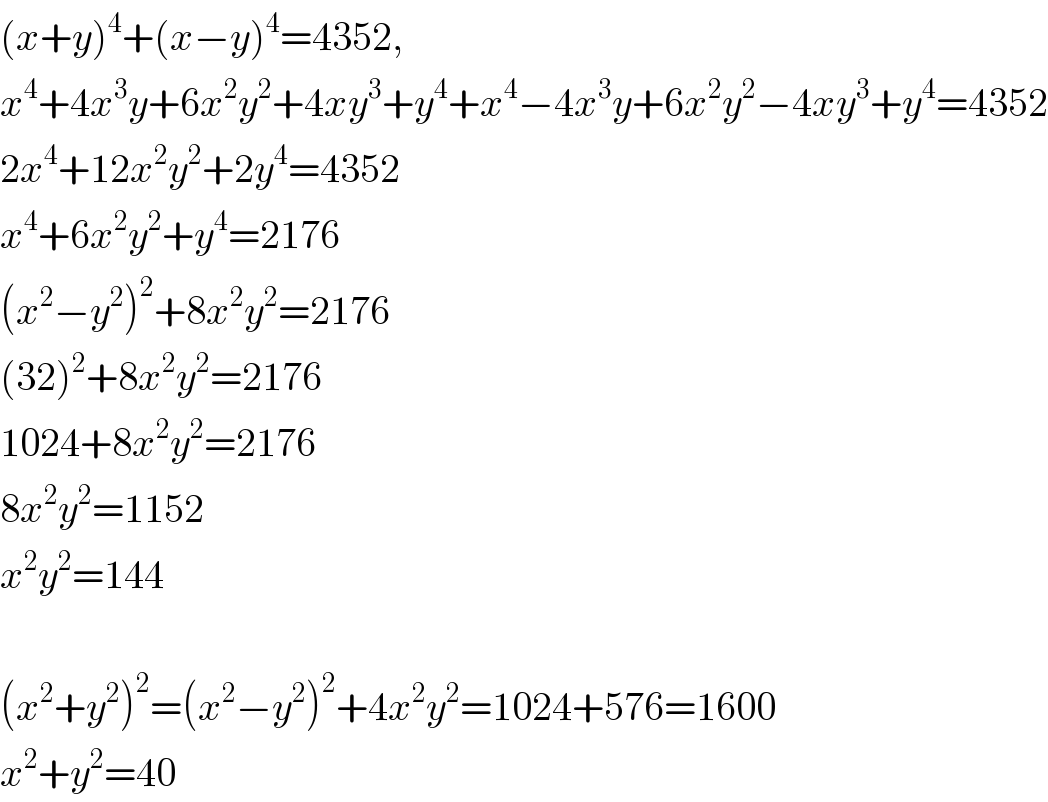
$$\left({x}+{y}\right)^{\mathrm{4}} +\left({x}−{y}\right)^{\mathrm{4}} =\mathrm{4352},\: \\ $$$${x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} {y}+\mathrm{6}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{4}{xy}^{\mathrm{3}} +{y}^{\mathrm{4}} +{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} {y}+\mathrm{6}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{4}{xy}^{\mathrm{3}} +{y}^{\mathrm{4}} =\mathrm{4352} \\ $$$$\mathrm{2}{x}^{\mathrm{4}} +\mathrm{12}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{4}} =\mathrm{4352} \\ $$$${x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} =\mathrm{2176} \\ $$$$\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{8}{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{2176} \\ $$$$\left(\mathrm{32}\right)^{\mathrm{2}} +\mathrm{8}{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{2176} \\ $$$$\mathrm{1024}+\mathrm{8}{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{2176} \\ $$$$\mathrm{8}{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{1152} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{144} \\ $$$$ \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} =\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{1024}+\mathrm{576}=\mathrm{1600} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{40} \\ $$
Commented by ZiYangLee last updated on 26/Sep/20

$$\mathrm{Thank}\:\mathrm{you}! \\ $$
Answered by Olaf last updated on 26/Sep/20
![(x+y)^4 +(x−y)^4 = [(x+y)^2 +(x−y)^2 ]^2 −2(x+y)^2 (x−y)^2 = (2x^2 +2y^2 )^2 −2(x^2 −y^2 )^2 = 4(x^2 +y^2 )^2 −2×32^2 = 4352 (x^2 +y^2 )^2 = ((4352+2048)/4) = ((6400)/4) = 1600 x^2 +y^2 = 40](Q115569.png)
$$\left({x}+{y}\right)^{\mathrm{4}} +\left({x}−{y}\right)^{\mathrm{4}} \:= \\ $$$$\left[\left({x}+{y}\right)^{\mathrm{2}} +\left({x}−{y}\right)^{\mathrm{2}} \right]^{\mathrm{2}} −\mathrm{2}\left({x}+{y}\right)^{\mathrm{2}} \left({x}−{y}\right)^{\mathrm{2}} \:= \\ $$$$\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{2}} \:= \\ $$$$\mathrm{4}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}×\mathrm{32}^{\mathrm{2}} \:=\:\mathrm{4352} \\ $$$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} \:=\:\frac{\mathrm{4352}+\mathrm{2048}}{\mathrm{4}}\:=\:\frac{\mathrm{6400}}{\mathrm{4}}\:=\:\mathrm{1600} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\mathrm{40} \\ $$
