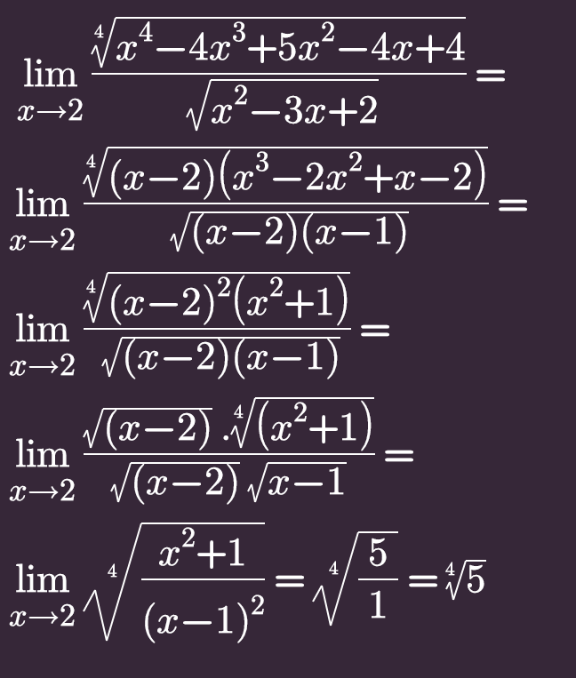Question Number 115551 by bemath last updated on 26/Sep/20
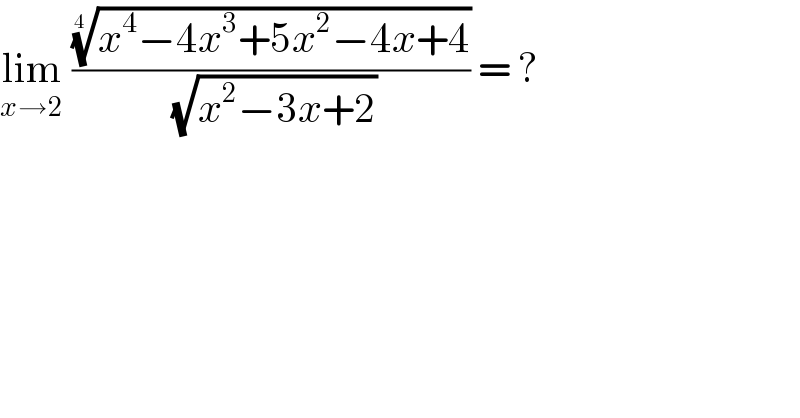
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{4}\:}]{{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}}}\:=\:? \\ $$
Answered by TANMAY PANACEA last updated on 26/Sep/20
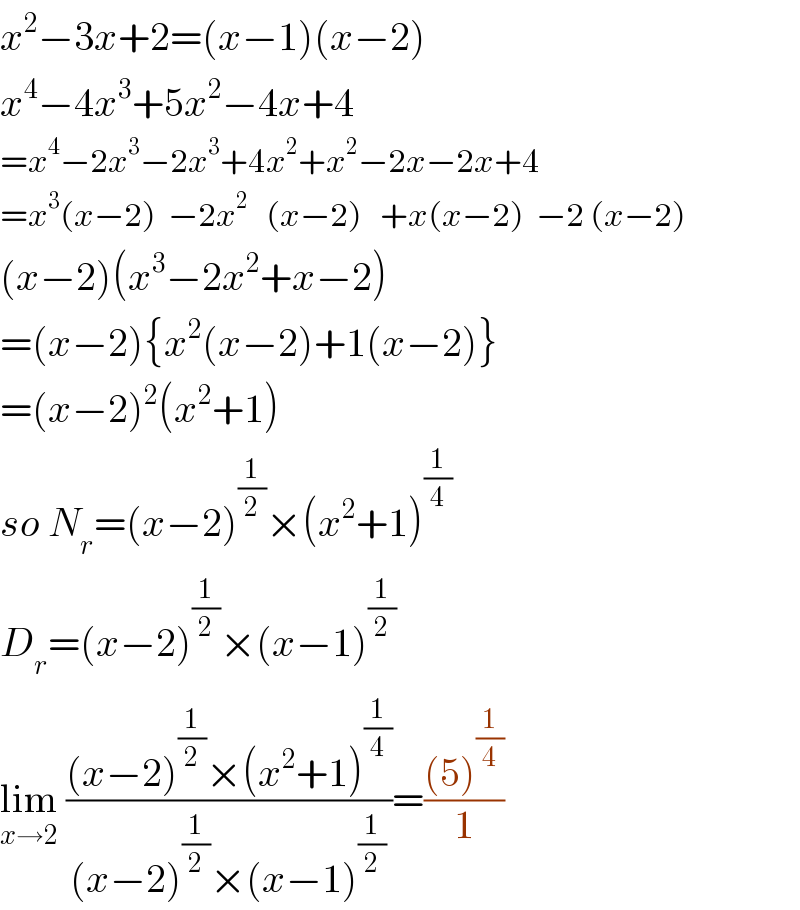
$${x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}=\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right) \\ $$$${x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4} \\ $$$$={x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{2}{x}+\mathrm{4} \\ $$$$={x}^{\mathrm{3}} \left({x}−\mathrm{2}\right)\:\:−\mathrm{2}{x}^{\mathrm{2}} \:\:\:\left({x}−\mathrm{2}\right)\:\:\:+{x}\left({x}−\mathrm{2}\right)\:\:−\mathrm{2}\:\left({x}−\mathrm{2}\right) \\ $$$$\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{2}\right) \\ $$$$=\left({x}−\mathrm{2}\right)\left\{{x}^{\mathrm{2}} \left({x}−\mathrm{2}\right)+\mathrm{1}\left({x}−\mathrm{2}\right)\right\} \\ $$$$=\left({x}−\mathrm{2}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${so}\:{N}_{{r}} =\left({x}−\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ×\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$${D}_{{r}} =\left({x}−\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ×\left({x}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\left({x}−\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ×\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }{\left({x}−\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} ×\left({x}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\left(\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }{\mathrm{1}} \\ $$
Commented by bemath last updated on 26/Sep/20

$${yess} \\ $$
Answered by bemath last updated on 26/Sep/20