
Question Number 11544 by Nayon last updated on 28/Mar/17
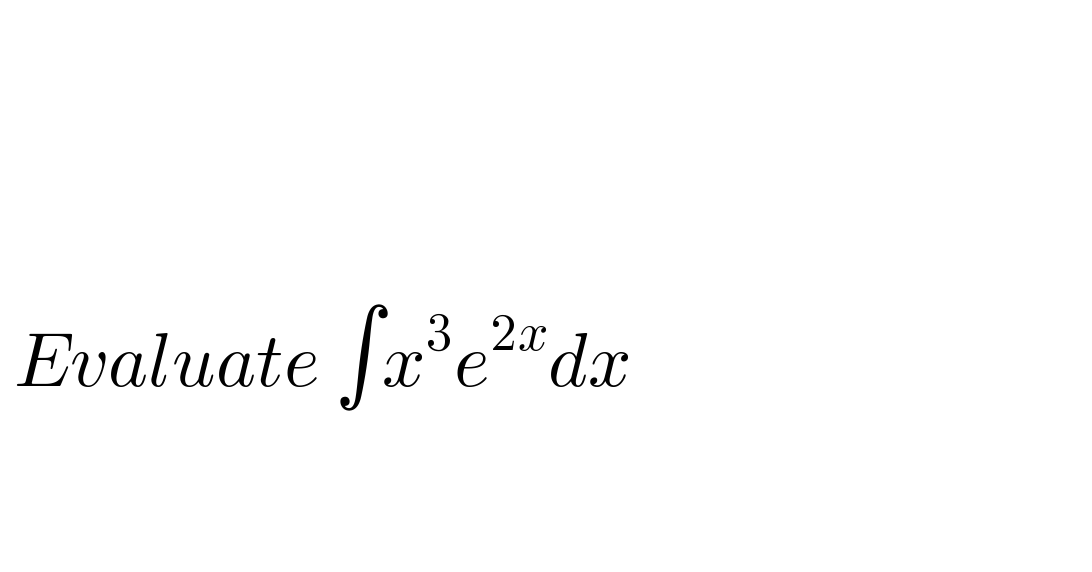
$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:{Evaluate}\:\int{x}^{\mathrm{3}} {e}^{\mathrm{2}{x}} {dx} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Answered by ajfour last updated on 28/Mar/17
![∫x^3 e^(2x) dx = x^3 e^(2x) /2 −∫(3x^2 )((e^(2x) /2))dx =f(x)−(3/2)∫x^2 e^(2x) dx = f(x)−(3/2){((x^2 e^(2x) )/2)−∫(2x)((e^(2x) /2))dx } =f(x)−(3/4)x^2 e^(2x) +(3/2)[ ((xe^(2x) )/2) −(1/2)∫e^(2x) dx ] = ((x^3 e^(2x) )/2)−(3/4)x^2 e^(2x) +(3/4)xe^(2x) −(3/8)e^(2x) +C =(e^(2x) /8) (4x^3 −6x^2 +6x−3 )+C](Q11554.png)
$$\int\mathrm{x}^{\mathrm{3}} \mathrm{e}^{\mathrm{2x}} \mathrm{dx}\:=\:\mathrm{x}^{\mathrm{3}} \mathrm{e}^{\mathrm{2x}} /\mathrm{2}\:−\int\left(\mathrm{3x}^{\mathrm{2}} \right)\left(\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{2}}\right)\mathrm{dx} \\ $$$$=\mathrm{f}\left(\mathrm{x}\right)−\frac{\mathrm{3}}{\mathrm{2}}\int\mathrm{x}^{\mathrm{2}} \mathrm{e}^{\mathrm{2x}} \mathrm{dx} \\ $$$$=\:\mathrm{f}\left(\mathrm{x}\right)−\frac{\mathrm{3}}{\mathrm{2}}\left\{\frac{\mathrm{x}^{\mathrm{2}} \mathrm{e}^{\mathrm{2x}} }{\mathrm{2}}−\int\left(\mathrm{2x}\right)\left(\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{2}}\right)\mathrm{dx}\:\right\} \\ $$$$=\mathrm{f}\left(\mathrm{x}\right)−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} \mathrm{e}^{\mathrm{2x}} \:+\frac{\mathrm{3}}{\mathrm{2}}\left[\:\frac{\mathrm{xe}^{\mathrm{2x}} }{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{e}^{\mathrm{2x}} \mathrm{dx}\:\right] \\ $$$$=\:\frac{\mathrm{x}^{\mathrm{3}} \mathrm{e}^{\mathrm{2x}} }{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} \mathrm{e}^{\mathrm{2x}} +\frac{\mathrm{3}}{\mathrm{4}}\mathrm{xe}^{\mathrm{2x}} −\frac{\mathrm{3}}{\mathrm{8}}\mathrm{e}^{\mathrm{2x}} \:+\mathrm{C} \\ $$$$=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{8}}\:\left(\mathrm{4x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} +\mathrm{6x}−\mathrm{3}\:\right)+\mathrm{C} \\ $$
