
Question Number 115418 by mohammad17 last updated on 25/Sep/20

Commented by mohammad17 last updated on 25/Sep/20
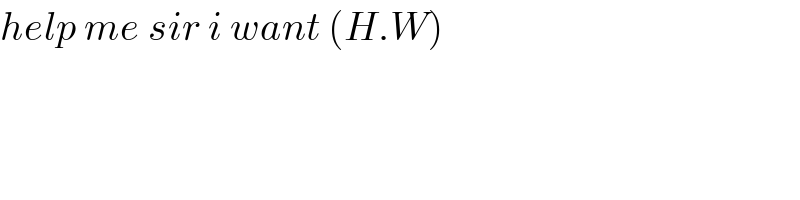
$${help}\:{me}\:{sir}\:{i}\:{want}\:\left({H}.{W}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20
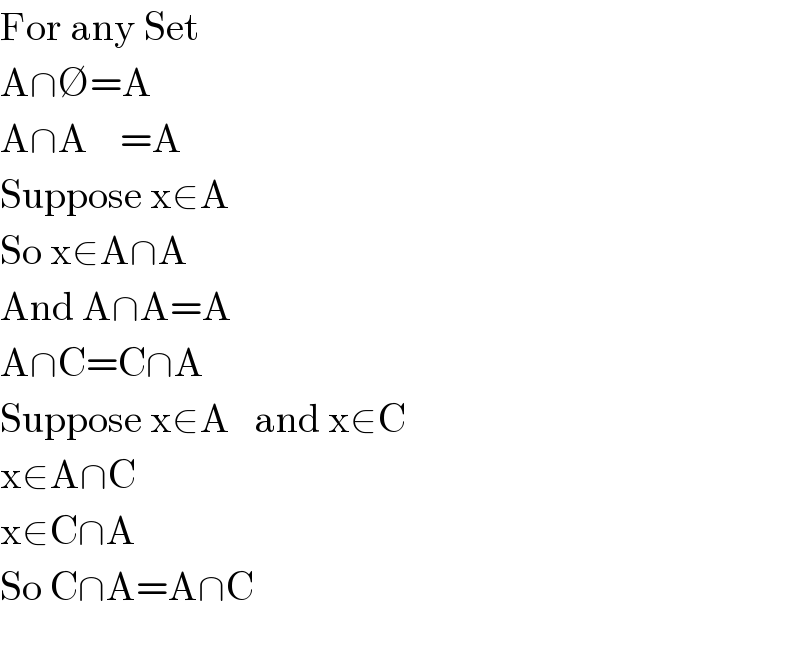
$$\mathrm{For}\:\mathrm{any}\:\mathrm{Set} \\ $$$$\mathrm{A}\cap\varnothing=\mathrm{A} \\ $$$$\mathrm{A}\cap\mathrm{A}\:\:\:\:=\mathrm{A} \\ $$$$\mathrm{Suppose}\:\mathrm{x}\in\mathrm{A}\: \\ $$$$\mathrm{So}\:\mathrm{x}\in\mathrm{A}\cap\mathrm{A} \\ $$$$\mathrm{And}\:\mathrm{A}\cap\mathrm{A}=\mathrm{A} \\ $$$$\mathrm{A}\cap\mathrm{C}=\mathrm{C}\cap\mathrm{A} \\ $$$$\mathrm{Suppose}\:\mathrm{x}\in\mathrm{A}\:\:\:\mathrm{and}\:\mathrm{x}\in\mathrm{C} \\ $$$$\mathrm{x}\in\mathrm{A}\cap\mathrm{C} \\ $$$$\mathrm{x}\in\mathrm{C}\cap\mathrm{A} \\ $$$$\mathrm{So}\:\mathrm{C}\cap\mathrm{A}=\mathrm{A}\cap\mathrm{C} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20

$$\mathrm{x}\:\mathrm{is}\:\mathrm{an}\:\mathrm{element}\:\mathrm{of}\:\mathrm{set}\:\mathrm{A}\:\left(\mathrm{x}\in\mathrm{A}\right) \\ $$$$\mathrm{And}\:\left(\mathrm{x}\in\mathrm{B}\right) \\ $$$$\mathrm{And}\:\mathrm{x}\in\left(\:\mathrm{A}\cap\mathrm{B}\:\right)\:\left(\mathrm{By}\:\mathrm{definition}\right) \\ $$$$\mathrm{And}\:\left(\mathrm{A}\cap\mathrm{B}\right)\subseteq\mathrm{A}\: \\ $$$$\mathrm{Also}\:\left(\mathrm{A}\cap\mathrm{B}\right)\subseteq\mathrm{B} \\ $$$$ \\ $$
Commented by mohammad17 last updated on 25/Sep/20
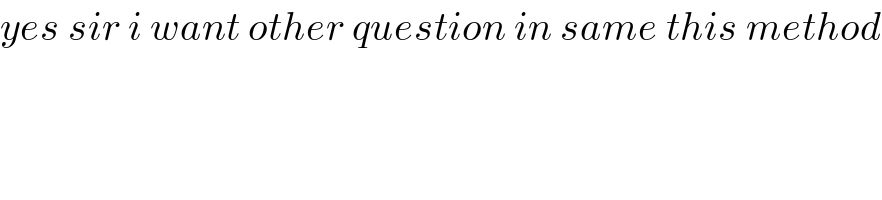
$${yes}\:{sir}\:{i}\:{want}\:{other}\:{question}\:{in}\:{same}\:{this}\:{method} \\ $$
Commented by Dwaipayan Shikari last updated on 25/Sep/20

$$\mathrm{It}\:\mathrm{is}\:\mathrm{better}\:\mathrm{to}\:\mathrm{use}\:\mathrm{Venn}\:\mathrm{diagram}\:\mathrm{in}\:\mathrm{Q7} \\ $$
Answered by MWSuSon last updated on 25/Sep/20
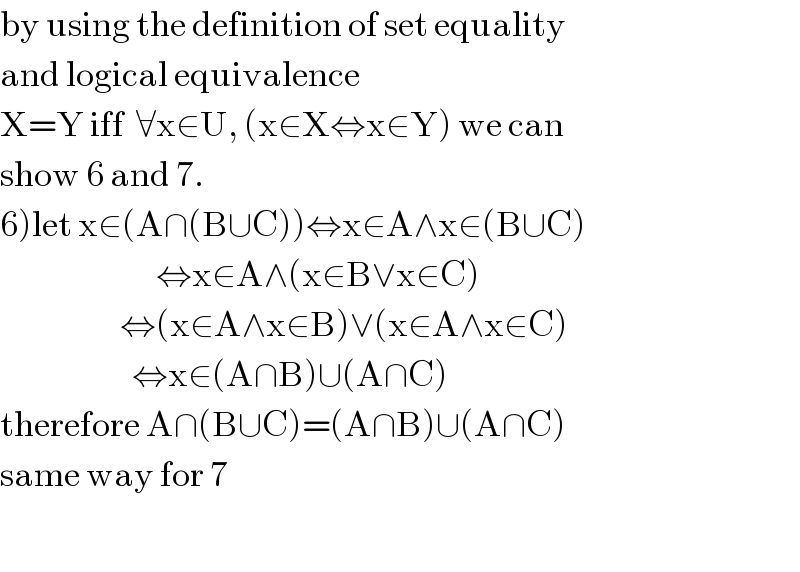
$$\mathrm{by}\:\mathrm{using}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of}\:\mathrm{set}\:\mathrm{equality} \\ $$$$\mathrm{and}\:\mathrm{logical}\:\mathrm{equivalence} \\ $$$$\mathrm{X}=\mathrm{Y}\:\mathrm{iff}\:\:\forall\mathrm{x}\in\mathrm{U},\:\left(\mathrm{x}\in\mathrm{X}\Leftrightarrow\mathrm{x}\in\mathrm{Y}\right)\:\mathrm{we}\:\mathrm{can} \\ $$$$\mathrm{show}\:\mathrm{6}\:\mathrm{and}\:\mathrm{7}. \\ $$$$\left.\mathrm{6}\right)\mathrm{let}\:\mathrm{x}\in\left(\mathrm{A}\cap\left(\mathrm{B}\cup\mathrm{C}\right)\right)\Leftrightarrow\mathrm{x}\in\mathrm{A}\wedge\mathrm{x}\in\left(\mathrm{B}\cup\mathrm{C}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\mathrm{x}\in\mathrm{A}\wedge\left(\mathrm{x}\in\mathrm{B}\vee\mathrm{x}\in\mathrm{C}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\left(\mathrm{x}\in\mathrm{A}\wedge\mathrm{x}\in\mathrm{B}\right)\vee\left(\mathrm{x}\in\mathrm{A}\wedge\mathrm{x}\in\mathrm{C}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\mathrm{x}\in\left(\mathrm{A}\cap\mathrm{B}\right)\cup\left(\mathrm{A}\cap\mathrm{C}\right) \\ $$$$\mathrm{therefore}\:\mathrm{A}\cap\left(\mathrm{B}\cup\mathrm{C}\right)=\left(\mathrm{A}\cap\mathrm{B}\right)\cup\left(\mathrm{A}\cap\mathrm{C}\right) \\ $$$$\mathrm{same}\:\mathrm{way}\:\mathrm{for}\:\mathrm{7} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
