
Question Number 115396 by Sudip last updated on 25/Sep/20

$$\mathrm{If}\:\mathrm{a}\:\mathrm{page}\:\mathrm{is}\:\mathrm{torn}\:\mathrm{from}\:\mathrm{the}\:\mathrm{middle}\:\mathrm{of}\:\mathrm{a}\:\mathrm{book},\:\mathrm{then} \\ $$$$\mathrm{the}\:\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{remaining}\:\mathrm{pages}\:\mathrm{is}\:\mathrm{718797}\:\mathrm{so} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{torn}\:\mathrm{pages}? \\ $$
Answered by PRITHWISH SEN 2 last updated on 25/Sep/20

$$\mathrm{901}\:\&\:\mathrm{902} \\ $$
Answered by TANMAY PANACEA last updated on 25/Sep/20
![S=(n/2)[2×1+(n−1)1] S=718797+x+x+1=((n^2 +n)/2) n^2 +n=2(2x+718798) wait...](Q115425.png)
$${S}=\frac{{n}}{\mathrm{2}}\left[\mathrm{2}×\mathrm{1}+\left({n}−\mathrm{1}\right)\mathrm{1}\right] \\ $$$${S}=\mathrm{718797}+{x}+{x}+\mathrm{1}=\frac{{n}^{\mathrm{2}} +{n}}{\mathrm{2}} \\ $$$${n}^{\mathrm{2}} +{n}=\mathrm{2}\left(\mathrm{2}{x}+\mathrm{718798}\right) \\ $$$${wait}... \\ $$
Answered by mr W last updated on 26/Sep/20
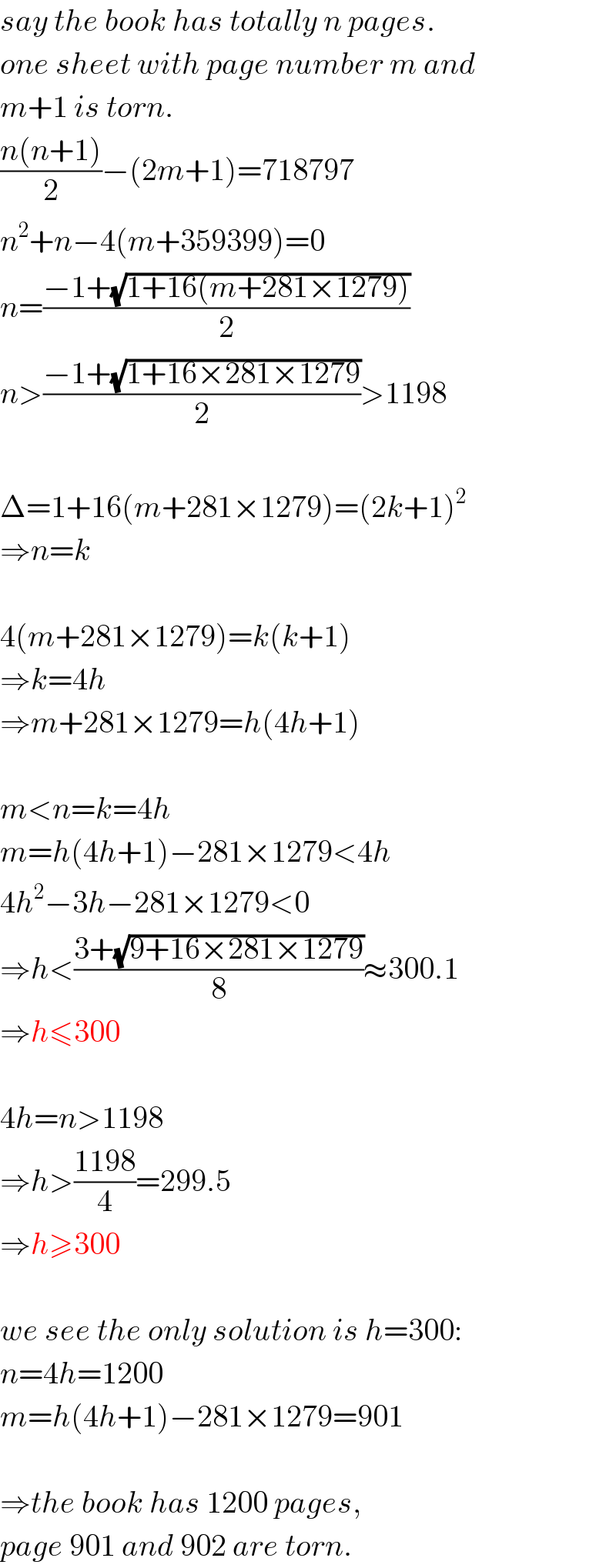
$${say}\:{the}\:{book}\:{has}\:{totally}\:{n}\:{pages}. \\ $$$${one}\:{sheet}\:{with}\:{page}\:{number}\:{m}\:{and} \\ $$$${m}+\mathrm{1}\:{is}\:{torn}. \\ $$$$\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}−\left(\mathrm{2}{m}+\mathrm{1}\right)=\mathrm{718797} \\ $$$${n}^{\mathrm{2}} +{n}−\mathrm{4}\left({m}+\mathrm{359399}\right)=\mathrm{0} \\ $$$${n}=\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{16}\left({m}+\mathrm{281}×\mathrm{1279}\right)}}{\mathrm{2}} \\ $$$${n}>\frac{−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{16}×\mathrm{281}×\mathrm{1279}}}{\mathrm{2}}>\mathrm{1198} \\ $$$$ \\ $$$$\Delta=\mathrm{1}+\mathrm{16}\left({m}+\mathrm{281}×\mathrm{1279}\right)=\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{n}={k} \\ $$$$ \\ $$$$\mathrm{4}\left({m}+\mathrm{281}×\mathrm{1279}\right)={k}\left({k}+\mathrm{1}\right) \\ $$$$\Rightarrow{k}=\mathrm{4}{h} \\ $$$$\Rightarrow{m}+\mathrm{281}×\mathrm{1279}={h}\left(\mathrm{4}{h}+\mathrm{1}\right) \\ $$$$ \\ $$$${m}<{n}={k}=\mathrm{4}{h} \\ $$$${m}={h}\left(\mathrm{4}{h}+\mathrm{1}\right)−\mathrm{281}×\mathrm{1279}<\mathrm{4}{h} \\ $$$$\mathrm{4}{h}^{\mathrm{2}} −\mathrm{3}{h}−\mathrm{281}×\mathrm{1279}<\mathrm{0} \\ $$$$\Rightarrow{h}<\frac{\mathrm{3}+\sqrt{\mathrm{9}+\mathrm{16}×\mathrm{281}×\mathrm{1279}}}{\mathrm{8}}\approx\mathrm{300}.\mathrm{1} \\ $$$$\Rightarrow{h}\leqslant\mathrm{300} \\ $$$$ \\ $$$$\mathrm{4}{h}={n}>\mathrm{1198} \\ $$$$\Rightarrow{h}>\frac{\mathrm{1198}}{\mathrm{4}}=\mathrm{299}.\mathrm{5} \\ $$$$\Rightarrow{h}\geqslant\mathrm{300} \\ $$$$ \\ $$$${we}\:{see}\:{the}\:{only}\:{solution}\:{is}\:{h}=\mathrm{300}: \\ $$$${n}=\mathrm{4}{h}=\mathrm{1200} \\ $$$${m}={h}\left(\mathrm{4}{h}+\mathrm{1}\right)−\mathrm{281}×\mathrm{1279}=\mathrm{901} \\ $$$$ \\ $$$$\Rightarrow{the}\:{book}\:{has}\:\mathrm{1200}\:{pages}, \\ $$$${page}\:\mathrm{901}\:{and}\:\mathrm{902}\:{are}\:{torn}. \\ $$
