
Question Number 115345 by bemath last updated on 25/Sep/20
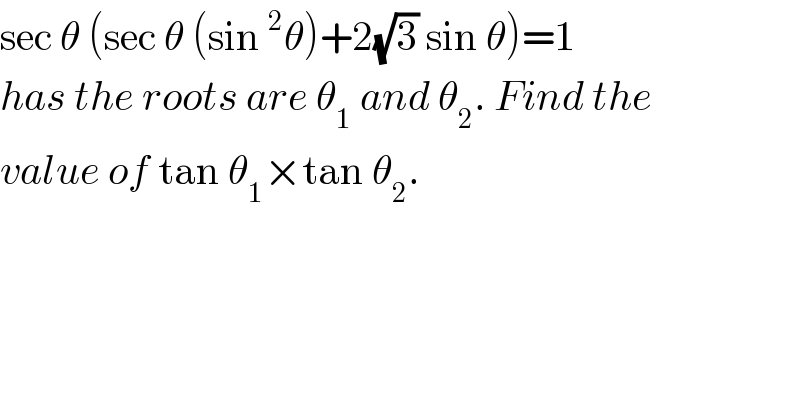
$$\mathrm{sec}\:\theta\:\left(\mathrm{sec}\:\theta\:\left(\mathrm{sin}\:^{\mathrm{2}} \theta\right)+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\right)=\mathrm{1} \\ $$$${has}\:{the}\:{roots}\:{are}\:\theta_{\mathrm{1}} \:{and}\:\theta_{\mathrm{2}} .\:{Find}\:{the} \\ $$$${value}\:{of}\:\mathrm{tan}\:\theta_{\mathrm{1}} ×\mathrm{tan}\:\theta_{\mathrm{2}} . \\ $$
Answered by bobhans last updated on 25/Sep/20
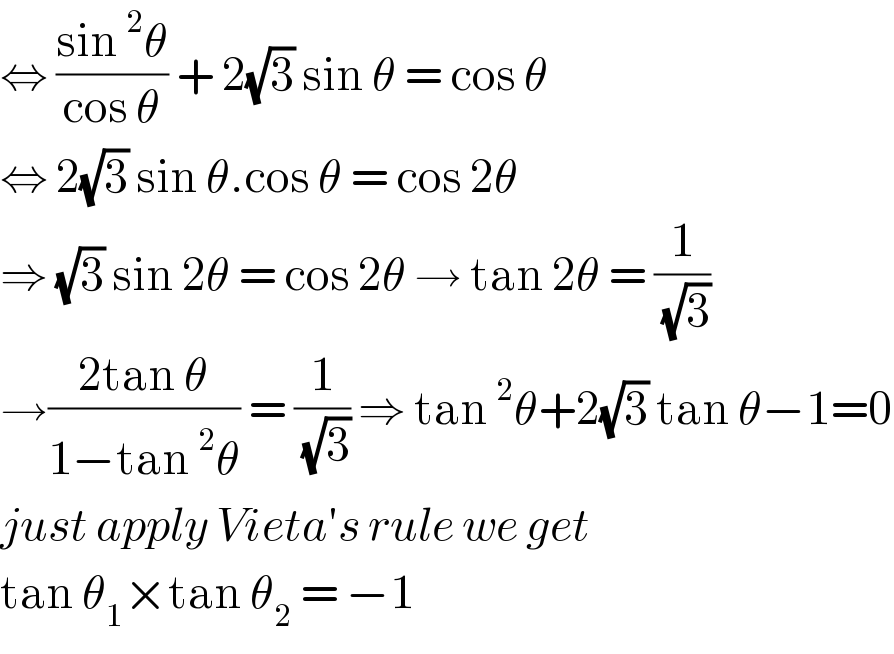
$$\Leftrightarrow\:\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{cos}\:\theta}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta\:=\:\mathrm{cos}\:\theta \\ $$$$\Leftrightarrow\:\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\theta.\mathrm{cos}\:\theta\:=\:\mathrm{cos}\:\mathrm{2}\theta\: \\ $$$$\Rightarrow\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{2}\theta\:=\:\mathrm{cos}\:\mathrm{2}\theta\:\rightarrow\:\mathrm{tan}\:\mathrm{2}\theta\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\rightarrow\frac{\mathrm{2tan}\:\theta}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \theta}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\Rightarrow\:\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{tan}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$${just}\:{apply}\:{Vieta}'{s}\:{rule}\:{we}\:{get}\: \\ $$$$\mathrm{tan}\:\theta_{\mathrm{1}} ×\mathrm{tan}\:\theta_{\mathrm{2}} \:=\:−\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20
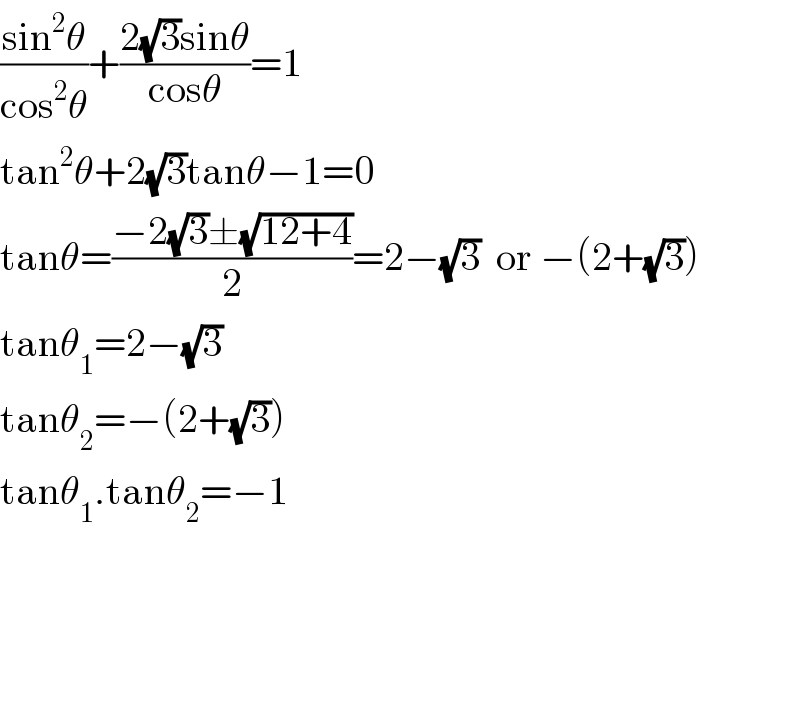
$$\frac{\mathrm{sin}^{\mathrm{2}} \theta}{\mathrm{cos}^{\mathrm{2}} \theta}+\frac{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\theta}{\mathrm{cos}\theta}=\mathrm{1} \\ $$$$\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{2}\sqrt{\mathrm{3}}\mathrm{tan}\theta−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{tan}\theta=\frac{−\mathrm{2}\sqrt{\mathrm{3}}\pm\sqrt{\mathrm{12}+\mathrm{4}}}{\mathrm{2}}=\mathrm{2}−\sqrt{\mathrm{3}}\:\:\mathrm{or}\:−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$\mathrm{tan}\theta_{\mathrm{1}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\mathrm{tan}\theta_{\mathrm{2}} =−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$\mathrm{tan}\theta_{\mathrm{1}} .\mathrm{tan}\theta_{\mathrm{2}} =−\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by MJS_new last updated on 25/Sep/20
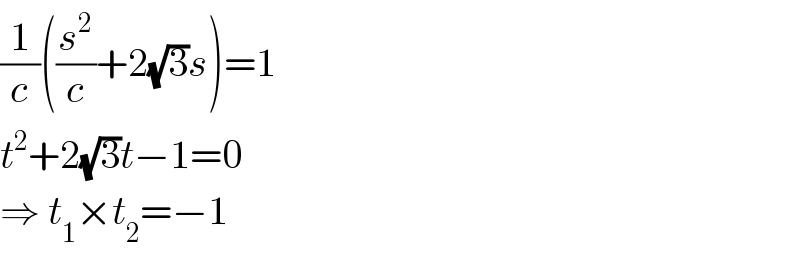
$$\frac{\mathrm{1}}{{c}}\left(\frac{{s}^{\mathrm{2}} }{{c}}+\mathrm{2}\sqrt{\mathrm{3}}{s}\right)=\mathrm{1} \\ $$$${t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{t}_{\mathrm{1}} ×{t}_{\mathrm{2}} =−\mathrm{1} \\ $$
