Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 115312 by naka3546 last updated on 25/Sep/20

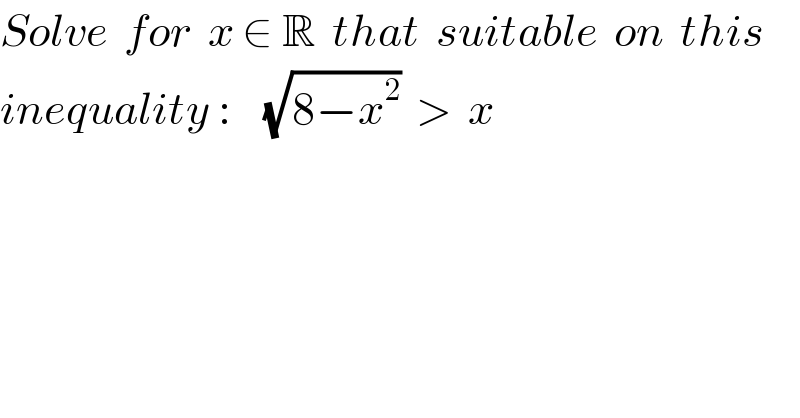
Solve for x ∈ R that suitable on this inequality : (√(8−x^2 )) > x

$${Solve}\:\:{for}\:\:{x}\:\in\:\mathbb{R}\:\:{that}\:\:{suitable}\:\:{on}\:\:{this} \\ $$ $${inequality}\::\:\:\:\:\sqrt{\mathrm{8}−{x}^{\mathrm{2}} }\:\:>\:\:{x} \\ $$

Commented bybemath last updated on 25/Sep/20

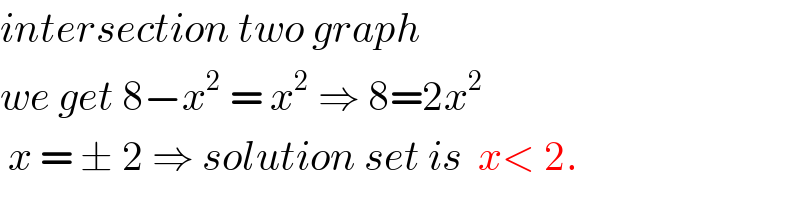
intersection two graph we get 8−x^2 = x^2 ⇒ 8=2x^2 x = ± 2 ⇒ solution set is x< 2.

$${intersection}\:{two}\:{graph} \\ $$ $${we}\:{get}\:\mathrm{8}−{x}^{\mathrm{2}} \:=\:{x}^{\mathrm{2}} \:\Rightarrow\:\mathrm{8}=\mathrm{2}{x}^{\mathrm{2}} \\ $$ $$\:{x}\:=\:\pm\:\mathrm{2}\:\Rightarrow\:{solution}\:{set}\:{is}\:\:{x}<\:\mathrm{2}. \\ $$

Commented byMJS_new last updated on 25/Sep/20

you are right, two graphs but f(x)=(√(8−x^2 )) is defined for −2(√2)≤x≤2(√2) and f(x)≥0. you are not allowed to square

$$\mathrm{you}\:\mathrm{are}\:\mathrm{right},\:\mathrm{two}\:\mathrm{graphs} \\ $$ $$\mathrm{but}\:{f}\left({x}\right)=\sqrt{\mathrm{8}−{x}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{2}\sqrt{\mathrm{2}} \\ $$ $$\mathrm{and}\:{f}\left({x}\right)\geqslant\mathrm{0}.\:\mathrm{you}\:\mathrm{are}\:\mathrm{not}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{square} \\ $$

Answered by john santu last updated on 25/Sep/20

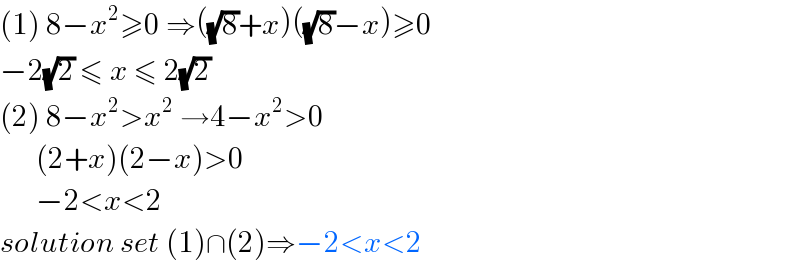
(1) 8−x^2 ≥0 ⇒((√8)+x)((√8)−x)≥0 −2(√2) ≤ x ≤ 2(√2) (2) 8−x^2 >x^2 →4−x^2 >0 (2+x)(2−x)>0 −2<x<2 solution set (1)∩(2)⇒−2<x<2

$$\left(\mathrm{1}\right)\:\mathrm{8}−{x}^{\mathrm{2}} \geqslant\mathrm{0}\:\Rightarrow\left(\sqrt{\mathrm{8}}+{x}\right)\left(\sqrt{\mathrm{8}}−{x}\right)\geqslant\mathrm{0} \\ $$ $$−\mathrm{2}\sqrt{\mathrm{2}}\:\leqslant\:{x}\:\leqslant\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$ $$\left(\mathrm{2}\right)\:\mathrm{8}−{x}^{\mathrm{2}} >{x}^{\mathrm{2}} \:\rightarrow\mathrm{4}−{x}^{\mathrm{2}} >\mathrm{0}\: \\ $$ $$\:\:\:\:\:\:\left(\mathrm{2}+{x}\right)\left(\mathrm{2}−{x}\right)>\mathrm{0}\: \\ $$ $$\:\:\:\:\:\:−\mathrm{2}<{x}<\mathrm{2} \\ $$ $${solution}\:{set}\:\left(\mathrm{1}\right)\cap\left(\mathrm{2}\right)\Rightarrow−\mathrm{2}<{x}<\mathrm{2} \\ $$

Commented bynaka3546 last updated on 25/Sep/20

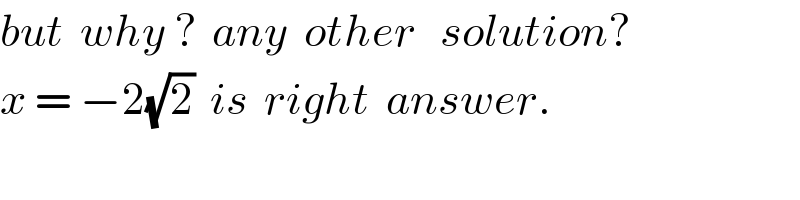
but why ? any other solution? x = −2(√2) is right answer.

$${but}\:\:{why}\:?\:\:{any}\:\:{other}\:\:\:{solution}? \\ $$ $${x}\:=\:−\mathrm{2}\sqrt{\mathrm{2}}\:\:{is}\:\:{right}\:\:{answer}. \\ $$

Commented byMJS_new last updated on 25/Sep/20

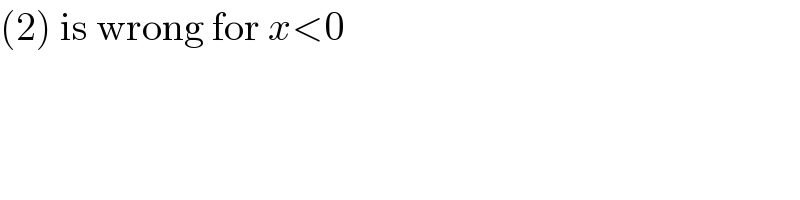
(2) is wrong for x<0

$$\left(\mathrm{2}\right)\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{for}\:{x}<\mathrm{0} \\ $$

Answered by MJS_new last updated on 25/Sep/20

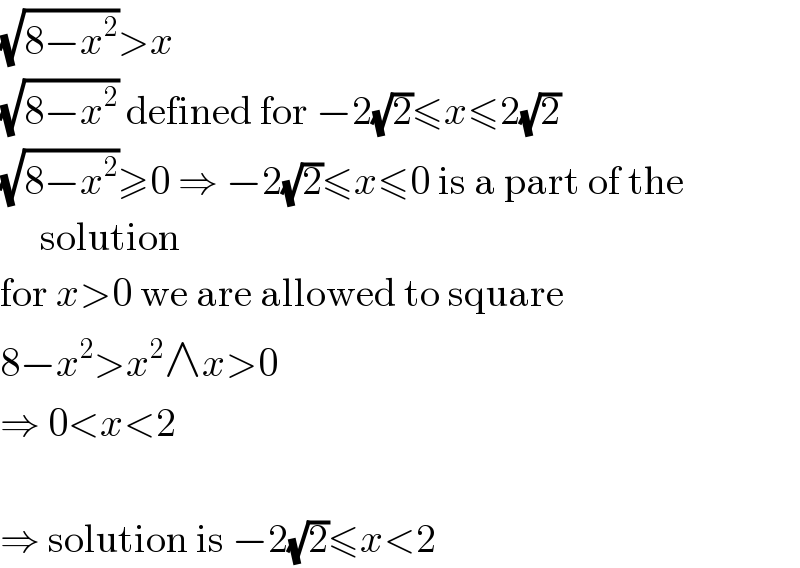
(√(8−x^2 ))>x (√(8−x^2 )) defined for −2(√2)≤x≤2(√2) (√(8−x^2 ))≥0 ⇒ −2(√2)≤x≤0 is a part of the solution for x>0 we are allowed to square 8−x^2 >x^2 ∧x>0 ⇒ 0<x<2 ⇒ solution is −2(√2)≤x<2

$$\sqrt{\mathrm{8}−{x}^{\mathrm{2}} }>{x} \\ $$ $$\sqrt{\mathrm{8}−{x}^{\mathrm{2}} }\:\mathrm{defined}\:\mathrm{for}\:−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{2}\sqrt{\mathrm{2}} \\ $$ $$\sqrt{\mathrm{8}−{x}^{\mathrm{2}} }\geqslant\mathrm{0}\:\Rightarrow\:−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{part}\:\mathrm{of}\:\mathrm{the} \\ $$ $$\:\:\:\:\:\mathrm{solution} \\ $$ $$\mathrm{for}\:{x}>\mathrm{0}\:\mathrm{we}\:\mathrm{are}\:\mathrm{allowed}\:\mathrm{to}\:\mathrm{square} \\ $$ $$\mathrm{8}−{x}^{\mathrm{2}} >{x}^{\mathrm{2}} \wedge{x}>\mathrm{0} \\ $$ $$\Rightarrow\:\mathrm{0}<{x}<\mathrm{2} \\ $$ $$ \\ $$ $$\Rightarrow\:\mathrm{solution}\:\mathrm{is}\:−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}<\mathrm{2} \\ $$

Answered by mr W last updated on 25/Sep/20

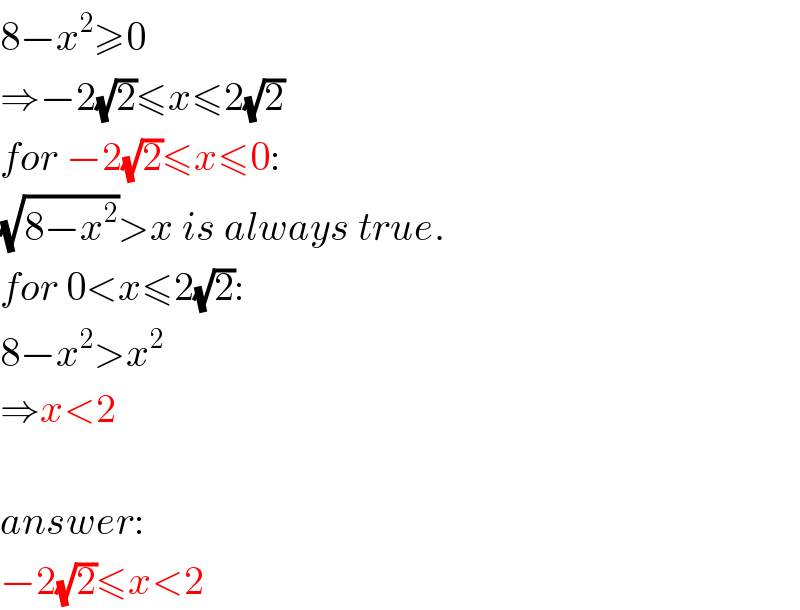
8−x^2 ≥0 ⇒−2(√2)≤x≤2(√2) for −2(√2)≤x≤0: (√(8−x^2 ))>x is always true. for 0<x≤2(√2): 8−x^2 >x^2 ⇒x<2 answer: −2(√2)≤x<2

$$\mathrm{8}−{x}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$ $$\Rightarrow−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{2}\sqrt{\mathrm{2}} \\ $$ $${for}\:−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}\leqslant\mathrm{0}: \\ $$ $$\sqrt{\mathrm{8}−{x}^{\mathrm{2}} }>{x}\:{is}\:{always}\:{true}. \\ $$ $${for}\:\mathrm{0}<{x}\leqslant\mathrm{2}\sqrt{\mathrm{2}}: \\ $$ $$\mathrm{8}−{x}^{\mathrm{2}} >{x}^{\mathrm{2}} \\ $$ $$\Rightarrow{x}<\mathrm{2} \\ $$ $$ \\ $$ $${answer}: \\ $$ $$−\mathrm{2}\sqrt{\mathrm{2}}\leqslant{x}<\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com