
Question Number 115301 by mathdave last updated on 24/Sep/20
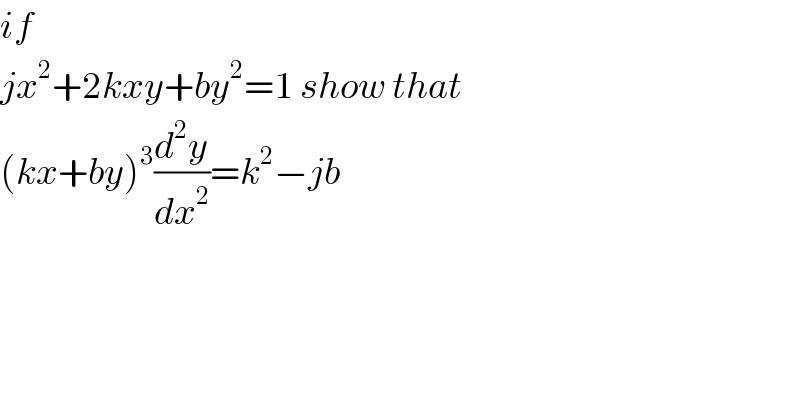
$${if}\: \\ $$$${jx}^{\mathrm{2}} +\mathrm{2}{kxy}+{by}^{\mathrm{2}} =\mathrm{1}\:{show}\:{that} \\ $$$$\left({kx}+{by}\right)^{\mathrm{3}} \frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }={k}^{\mathrm{2}} −{jb} \\ $$
Answered by 1549442205PVT last updated on 25/Sep/20

$${jx}^{\mathrm{2}} +\mathrm{2}{kxy}+{by}^{\mathrm{2}} =\mathrm{1}\Leftrightarrow\mathrm{by}^{\mathrm{2}} +\mathrm{2kxy}+\mathrm{jx}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\Delta'=\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b} \\ $$$$\mathrm{y}=\frac{−\mathrm{kx}\pm\sqrt{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}}}{\mathrm{b}}\left(\mathrm{1}\right) \\ $$$$\mathrm{y}'=\left(−\mathrm{k}\pm\frac{\left(\mathrm{k}^{\mathrm{2}} −\mathrm{jb}\right)\mathrm{x}}{\:\sqrt{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}}}\right)/\mathrm{b} \\ $$$$\mathrm{y}''=\pm\left(\frac{\left(\mathrm{k}^{\mathrm{2}} −\mathrm{jb}\right)\sqrt{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}}−\left(\mathrm{k}^{\mathrm{2}} −\mathrm{jb}\right)\mathrm{x}.\frac{\left(\mathrm{k}^{\mathrm{2}} −\mathrm{jb}\right)\mathrm{x}}{\:\sqrt{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}}}}{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}}\right)/\mathrm{b} \\ $$$$=\pm\left(\frac{\left(\mathrm{k}^{\mathrm{2}} −\mathrm{jb}\right)\left(\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}\right)−\left(\mathrm{k}^{\mathrm{2}} −\mathrm{jb}\right)^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{b}\left(\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}\right)\sqrt{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}}}\:\right)\:\: \\ $$$$=\pm\left(\frac{\left(\mathrm{k}^{\mathrm{2}} −\mathrm{jb}\right)}{\left(\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}\right)\sqrt{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}}}\right)\left(\mathrm{2}\right) \\ $$$$\mathrm{From}\left(\mathrm{1}\right)\mathrm{we}\:\mathrm{have}\: \\ $$$$\mathrm{kx}+\mathrm{by}=\pm\sqrt{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}} \\ $$$$\Rightarrow\left(\mathrm{kx}+\mathrm{by}\right)^{\mathrm{3}} =\left(\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}\right)\sqrt{\mathrm{k}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} −\mathrm{jbx}^{\mathrm{2}} +\mathrm{b}}\left(\mathrm{3}\right) \\ $$$$\mathrm{Replace}\:\left(\mathrm{3}\right)\:\mathrm{into}\:\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\left(\boldsymbol{\mathrm{kx}}+\boldsymbol{\mathrm{by}}\right)^{\mathrm{3}} \boldsymbol{\mathrm{y}}''=\boldsymbol{\mathrm{k}}^{\mathrm{2}} −\boldsymbol{\mathrm{jb}}\:\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right)\: \\ $$
Answered by Dwaipayan Shikari last updated on 25/Sep/20

$$\mathrm{jx}^{\mathrm{2}} +\mathrm{2kxy}+\mathrm{by}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{2jx}+\mathrm{2ky}+\mathrm{2kx}\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{2by}\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{0}\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=−\frac{\mathrm{jx}+\mathrm{ky}}{\mathrm{kx}+\mathrm{by}} \\ $$$$\mathrm{2j}+\mathrm{2k}.\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{2kx}\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{2k}.\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{2by}\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{2b}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{j}+\mathrm{2k}\frac{\mathrm{dy}}{\mathrm{dx}}+\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\left(\mathrm{kx}+\mathrm{by}\right)+\mathrm{b}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\left(\mathrm{kx}+\mathrm{by}\right)=−\mathrm{b}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} +\mathrm{2k}.\frac{\mathrm{jx}+\mathrm{ky}}{\mathrm{kx}+\mathrm{by}}−\mathrm{j} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\left(\mathrm{kx}+\mathrm{by}\right)=−\mathrm{b}\left(\frac{\mathrm{jx}+\mathrm{ky}}{\mathrm{kx}+\mathrm{by}}\right)^{\mathrm{2}} +\mathrm{2k}\frac{\mathrm{jx}+\mathrm{ky}}{\mathrm{kx}+\mathrm{by}}−\mathrm{j} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\left(\mathrm{kx}+\mathrm{by}\right)^{\mathrm{3}} =−\mathrm{b}\left(\mathrm{jx}+\mathrm{ky}\right)^{\mathrm{2}} +\mathrm{2k}\left(\mathrm{jx}+\mathrm{ky}\right)\left(\mathrm{kx}+\mathrm{by}\right)−\mathrm{j}\left(\mathrm{kx}+\mathrm{by}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\left(\mathrm{kx}+\mathrm{by}\right)^{\mathrm{3}} =\mathrm{k}^{\mathrm{2}} −\mathrm{jb}\:\left(\mathrm{After}\:\mathrm{simplifying}\right) \\ $$$$ \\ $$
