
Question Number 115294 by ZiYangLee last updated on 24/Sep/20
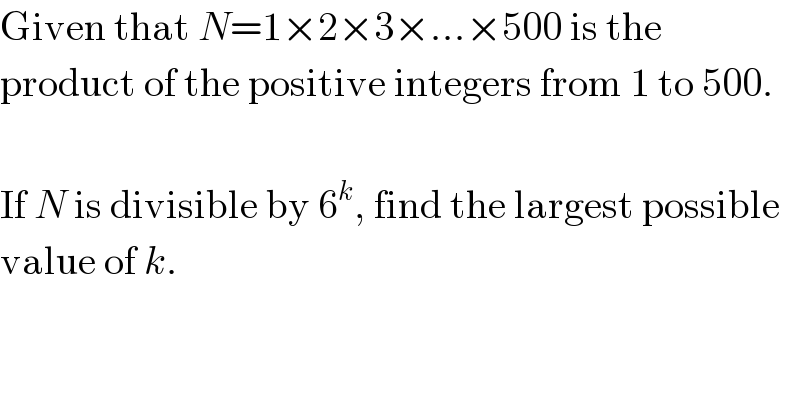
$$\mathrm{Given}\:\mathrm{that}\:{N}=\mathrm{1}×\mathrm{2}×\mathrm{3}×...×\mathrm{500}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{product}\:\mathrm{of}\:\mathrm{the}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{500}. \\ $$$$ \\ $$$$\mathrm{If}\:{N}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{6}^{{k}} ,\:\mathrm{find}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{possible} \\ $$$$\mathrm{value}\:\mathrm{of}\:{k}. \\ $$
Answered by Olaf last updated on 25/Sep/20

$$\mathrm{N}\:=\:\mathrm{500}! \\ $$$$\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8}...\mathrm{498},\mathrm{500}\:\mathrm{are}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2} \\ $$$$\left(\mathrm{250}\:\mathrm{numbers}\right) \\ $$$$\mathrm{3},\mathrm{6},\mathrm{9},\mathrm{12}...\mathrm{495},\mathrm{498}\:\mathrm{are}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3} \\ $$$$\mathrm{3}\:=\:\mathrm{3}×\mathrm{1} \\ $$$$\mathrm{6}\:=\:\mathrm{3}×\mathrm{2} \\ $$$$... \\ $$$$\mathrm{498}\:=\:\mathrm{3}×\mathrm{166} \\ $$$$\left(\mathrm{166}\:\mathrm{numbers}\right) \\ $$$$ \\ $$$$\mathrm{250}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2} \\ $$$$\mathrm{166}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{3} \\ $$$$\mathrm{6}^{{k}} \:=\:\mathrm{2}^{{k}} ×\mathrm{3}^{{k}} \::\:{k}_{{max}} \:=\:\mathrm{166} \\ $$$$\boldsymbol{\mathrm{Sorry}}\:\boldsymbol{\mathrm{but}}\:\boldsymbol{\mathrm{i}}'\boldsymbol{\mathrm{m}}\:\boldsymbol{\mathrm{wrong}}. \\ $$$$\boldsymbol{\mathrm{see}}\:\boldsymbol{\mathrm{mr}}\:\boldsymbol{\mathrm{W}}. \\ $$
Answered by mr W last updated on 25/Sep/20

$$\mathrm{2},\mathrm{2}×\mathrm{2},\mathrm{3}×\mathrm{2},...,\mathrm{250}×\mathrm{2}\:\Rightarrow\mathrm{2}^{\mathrm{250}×\mathrm{1}} \\ $$$$\mathrm{2}^{\mathrm{2}} ,\mathrm{2}×\mathrm{2}^{\mathrm{2}} ,\mathrm{3}×\mathrm{2}^{\mathrm{2}} ,...,\mathrm{125}×\mathrm{2}^{\mathrm{2}} \:\Rightarrow\mathrm{2}^{\mathrm{125}×\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{3}} ,\mathrm{2}×\mathrm{2}^{\mathrm{3}} ,\mathrm{3}×\mathrm{2}^{\mathrm{3}} ,...,\mathrm{62}×\mathrm{2}^{\mathrm{3}} \:\Rightarrow\mathrm{2}^{\mathrm{62}×\mathrm{3}} \\ $$$$\mathrm{2}^{\mathrm{4}} ,\mathrm{2}×\mathrm{2}^{\mathrm{4}} ,\mathrm{3}×\mathrm{2}^{\mathrm{4}} ,...,\mathrm{31}×\mathrm{2}^{\mathrm{4}} \:\Rightarrow\mathrm{2}^{\mathrm{31}×\mathrm{4}} \\ $$$$\mathrm{2}^{\mathrm{5}} ,\mathrm{2}×\mathrm{2}^{\mathrm{5}} ,\mathrm{3}×\mathrm{2}^{\mathrm{5}} ,...,\mathrm{15}×\mathrm{2}^{\mathrm{5}} \:\Rightarrow\mathrm{2}^{\mathrm{15}×\mathrm{5}} \\ $$$$\mathrm{2}^{\mathrm{6}} ,\mathrm{2}×\mathrm{2}^{\mathrm{6}} ,\mathrm{3}×\mathrm{2}^{\mathrm{6}} ,...,\mathrm{7}×\mathrm{2}^{\mathrm{6}} \:\Rightarrow\mathrm{2}^{\mathrm{7}×\mathrm{6}} \\ $$$$\mathrm{2}^{\mathrm{7}} ,\mathrm{2}×\mathrm{2}^{\mathrm{7}} ,\mathrm{3}×\mathrm{2}^{\mathrm{7}} ,...,\mathrm{3}×\mathrm{2}^{\mathrm{7}} \:\Rightarrow\mathrm{2}^{\mathrm{3}×\mathrm{7}} \\ $$$$\mathrm{2}^{\mathrm{8}} \:\Rightarrow\mathrm{2}^{\mathrm{1}×\mathrm{8}} \\ $$$$\mathrm{250}+\mathrm{125}+\mathrm{62}+\mathrm{31}+\mathrm{15}+\mathrm{7}+\mathrm{3}+\mathrm{1}=\mathrm{494} \\ $$$$\Rightarrow\mathrm{500}!\:{contains}\:\mathrm{2}^{\mathrm{494}} \\ $$$$ \\ $$$$\mathrm{3},\mathrm{2}×\mathrm{3},\mathrm{3}×\mathrm{3},...,\mathrm{166}×\mathrm{3}\:\Rightarrow\mathrm{3}^{\mathrm{166}×\mathrm{1}} \\ $$$$\mathrm{3}^{\mathrm{2}} ,\mathrm{2}×\mathrm{3}^{\mathrm{2}} ,\mathrm{3}×\mathrm{3}^{\mathrm{2}} ,...,\mathrm{55}×\mathrm{3}^{\mathrm{2}} \:\Rightarrow\mathrm{3}^{\mathrm{55}×\mathrm{2}} \\ $$$$\mathrm{3}^{\mathrm{3}} ,\mathrm{2}×\mathrm{3}^{\mathrm{3}} ,\mathrm{3}×\mathrm{3}^{\mathrm{3}} ,...,\mathrm{18}×\mathrm{3}^{\mathrm{3}} \:\Rightarrow\mathrm{3}^{\mathrm{18}×\mathrm{3}} \\ $$$$\mathrm{3}^{\mathrm{4}} ,\mathrm{2}×\mathrm{3}^{\mathrm{4}} ,\mathrm{3}×\mathrm{3}^{\mathrm{4}} ,...,\mathrm{6}×\mathrm{3}^{\mathrm{4}} \:\Rightarrow\mathrm{3}^{\mathrm{6}×\mathrm{4}} \\ $$$$\mathrm{3}^{\mathrm{5}} ,\mathrm{2}×\mathrm{3}^{\mathrm{5}} \:\Rightarrow\mathrm{3}^{\mathrm{2}×\mathrm{5}} \\ $$$$\mathrm{166}+\mathrm{55}+\mathrm{18}+\mathrm{6}+\mathrm{2}=\mathrm{247} \\ $$$$\Rightarrow\mathrm{500}!\:{contains}\:\mathrm{3}^{\mathrm{247}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{500}!\:{contains}\:\mathrm{2}^{\mathrm{494}} ×\mathrm{3}^{\mathrm{247}} \\ $$$$\Rightarrow\mathrm{500}!\:{contains}\:\mathrm{6}^{\mathrm{247}} \\ $$$$\Rightarrow{k}_{{max}} =\mathrm{247} \\ $$
Commented by Olaf last updated on 25/Sep/20

$$\mathrm{Mister}\:\mathrm{W}\:\mathrm{you}\:\mathrm{are}\:\mathrm{wright}. \\ $$$$\mathrm{Good}\:\mathrm{job}\:! \\ $$
Commented by mr W last updated on 25/Sep/20

$${i}\:{think}\:{we}\:{can}\:{generally}\:{do}\:{like}\:{this}: \\ $$$${to}\:{get}\:{k}\:{such}\:{that}\:{n}!\:{is}\:{divisible}\:{by} \\ $$$${p}^{{k}} \:{where}\:{p}={prime}, \\ $$$${k}=\lfloor\frac{{n}}{{p}}\rfloor+\lfloor\frac{{n}}{{p}^{\mathrm{2}} }\rfloor+\lfloor\frac{{n}}{{p}^{\mathrm{3}} }\rfloor+... \\ $$$$ \\ $$$${for}\:{example}\:{n}=\mathrm{500},\:{p}=\mathrm{7} \\ $$$${k}=\lfloor\frac{\mathrm{500}}{\mathrm{7}}\rfloor+\lfloor\frac{\mathrm{500}}{\mathrm{7}^{\mathrm{2}} }\rfloor+\lfloor\frac{\mathrm{500}}{\mathrm{7}^{\mathrm{3}} }\rfloor+... \\ $$$$=\mathrm{71}+\mathrm{10}+\mathrm{1} \\ $$$$=\mathrm{82} \\ $$$$\Rightarrow\mathrm{500}!\:{contains}\:\mathrm{7}^{\mathrm{82}} \\ $$$$ \\ $$$${for}\:{example}\:{n}=\mathrm{500},\:{p}=\mathrm{3} \\ $$$${k}=\lfloor\frac{\mathrm{500}}{\mathrm{3}}\rfloor+\lfloor\frac{\mathrm{500}}{\mathrm{3}^{\mathrm{2}} }\rfloor+\lfloor\frac{\mathrm{500}}{\mathrm{3}^{\mathrm{3}} }\rfloor+... \\ $$$$=\mathrm{166}+\mathrm{55}+\mathrm{18}+\mathrm{6}+\mathrm{2} \\ $$$$=\mathrm{247} \\ $$$$\Rightarrow\mathrm{500}!\:{contains}\:\mathrm{3}^{\mathrm{247}} \\ $$
Commented by ZiYangLee last updated on 26/Sep/20

$$\mathrm{Wow}!!!\: \\ $$
Commented by Lordose last updated on 01/Oct/20

$$\mathrm{Thanks}\:\mathrm{sir}\:\mathrm{Mr}\:\mathrm{W} \\ $$
