
Question Number 115268 by bobhans last updated on 24/Sep/20
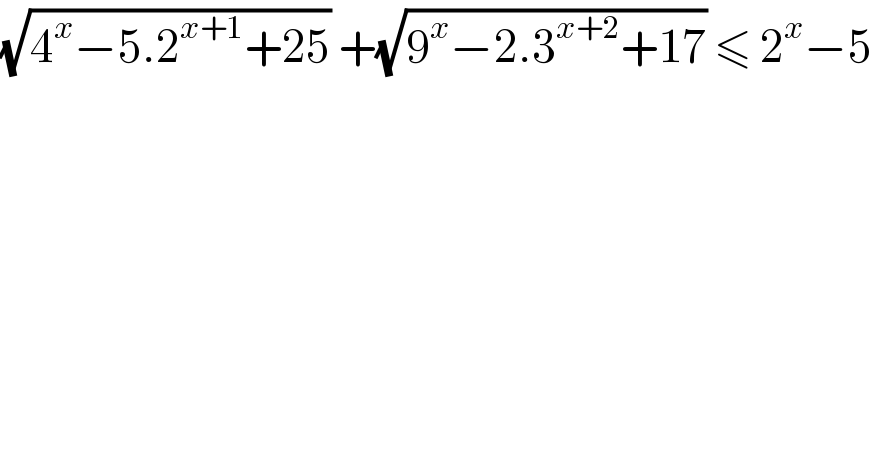
$$\sqrt{\mathrm{4}^{{x}} −\mathrm{5}.\mathrm{2}^{{x}+\mathrm{1}} +\mathrm{25}}\:+\sqrt{\mathrm{9}^{{x}} −\mathrm{2}.\mathrm{3}^{{x}+\mathrm{2}} +\mathrm{17}}\:\leqslant\:\mathrm{2}^{{x}} −\mathrm{5} \\ $$
Answered by john santu last updated on 24/Sep/20
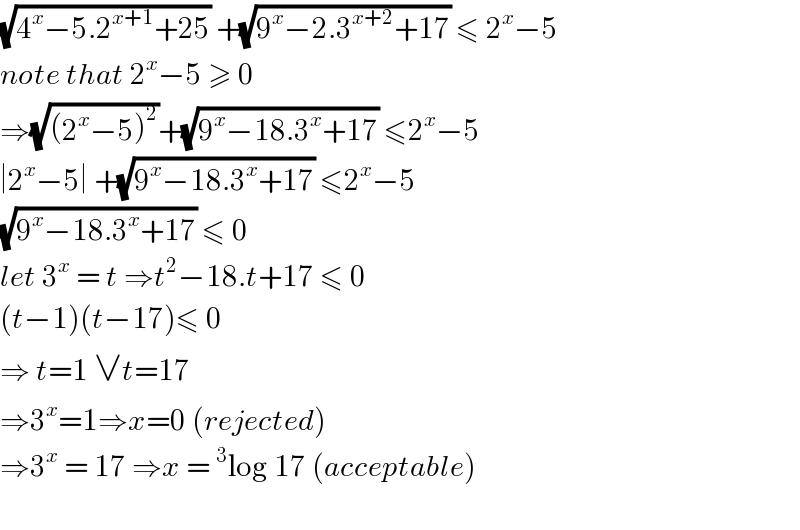
$$\sqrt{\mathrm{4}^{{x}} −\mathrm{5}.\mathrm{2}^{{x}+\mathrm{1}} +\mathrm{25}}\:+\sqrt{\mathrm{9}^{{x}} −\mathrm{2}.\mathrm{3}^{{x}+\mathrm{2}} +\mathrm{17}}\:\leqslant\:\mathrm{2}^{{x}} −\mathrm{5} \\ $$$${note}\:{that}\:\mathrm{2}^{{x}} −\mathrm{5}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow\sqrt{\left(\mathrm{2}^{{x}} −\mathrm{5}\right)^{\mathrm{2}} }+\sqrt{\mathrm{9}^{{x}} −\mathrm{18}.\mathrm{3}^{{x}} +\mathrm{17}}\:\leqslant\mathrm{2}^{{x}} −\mathrm{5} \\ $$$$\mid\mathrm{2}^{{x}} −\mathrm{5}\mid\:+\sqrt{\mathrm{9}^{{x}} −\mathrm{18}.\mathrm{3}^{{x}} +\mathrm{17}}\:\leqslant\mathrm{2}^{{x}} −\mathrm{5} \\ $$$$\sqrt{\mathrm{9}^{{x}} −\mathrm{18}.\mathrm{3}^{{x}} +\mathrm{17}}\:\leqslant\:\mathrm{0} \\ $$$${let}\:\mathrm{3}^{{x}} \:=\:{t}\:\Rightarrow{t}^{\mathrm{2}} −\mathrm{18}.{t}+\mathrm{17}\:\leqslant\:\mathrm{0} \\ $$$$\left({t}−\mathrm{1}\right)\left({t}−\mathrm{17}\right)\leqslant\:\mathrm{0} \\ $$$$\Rightarrow\:{t}=\mathrm{1}\:\vee{t}=\mathrm{17} \\ $$$$\Rightarrow\mathrm{3}^{{x}} =\mathrm{1}\Rightarrow{x}=\mathrm{0}\:\left({rejected}\right) \\ $$$$\Rightarrow\mathrm{3}^{{x}} \:=\:\mathrm{17}\:\Rightarrow{x}\:=\:^{\mathrm{3}} \mathrm{log}\:\mathrm{17}\:\left({acceptable}\right) \\ $$$$ \\ $$
