
Question Number 115258 by bobhans last updated on 24/Sep/20
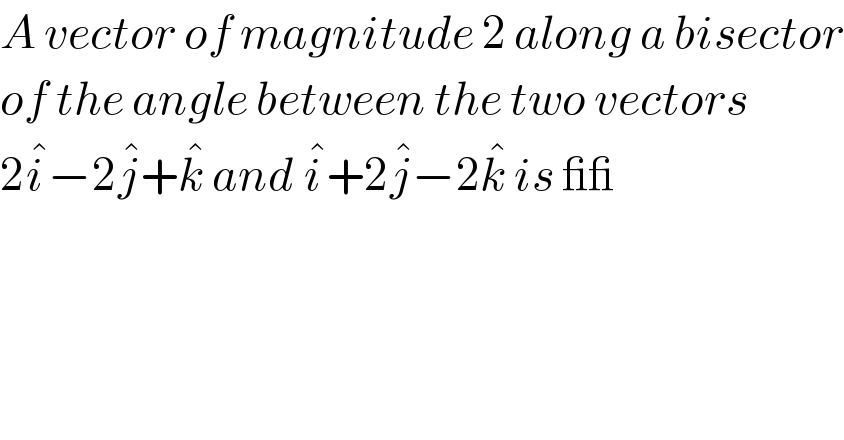
$${A}\:{vector}\:{of}\:{magnitude}\:\mathrm{2}\:{along}\:{a}\:{bisector} \\ $$$${of}\:{the}\:{angle}\:{between}\:{the}\:{two}\:{vectors} \\ $$$$\mathrm{2}\hat {{i}}−\mathrm{2}\hat {{j}}+\hat {{k}}\:{and}\:\hat {{i}}+\mathrm{2}\hat {{j}}−\mathrm{2}\hat {{k}}\:{is}\:\_\_ \\ $$
Answered by bemath last updated on 24/Sep/20

$${let}\:\overset{\rightarrow} {{a}}=\left(\mathrm{2},−\mathrm{2},\mathrm{1}\right)\:\&\:\overset{\rightarrow} {{b}}=\left(\mathrm{1},\mathrm{2},−\mathrm{2}\right) \\ $$$$\Rightarrow{vector}\:{along}\:{bisector}\:{is}\:{given} \\ $$$${by}\:\frac{\overset{\rightarrow} {{a}}}{\mid\overset{\rightarrow} {{a}}\mid}\:\pm\:\frac{\overset{\rightarrow} {{b}}}{\mid\overset{\rightarrow} {{b}}\mid}\:=\:\frac{\left(\mathrm{2},−\mathrm{2},\mathrm{1}\right)}{\mathrm{3}}\:\pm\:\frac{\left(\mathrm{1},\mathrm{2},−\mathrm{2}\right)}{\mathrm{3}} \\ $$$$=\:\left(\mathrm{1},\mathrm{0},−\frac{\mathrm{1}}{\mathrm{3}}\right)\:{or}\:\left(\frac{\mathrm{1}}{\mathrm{3}},−\frac{\mathrm{4}}{\mathrm{3}},\mathrm{1}\right) \\ $$$${Required}\:{vector}\:{are}\: \\ $$$$\left({i}\right)\:\mathrm{2}.\frac{\left(\mathrm{1},\mathrm{0},−\frac{\mathrm{1}}{\mathrm{3}}\right)}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{9}}}}\:=\:\frac{\left(\mathrm{6},\mathrm{0},−\mathrm{2}\right)}{\:\sqrt{\mathrm{10}}} \\ $$$$\left({ii}\right)\:\mathrm{2}.\frac{\left(\frac{\mathrm{1}}{\mathrm{3}},−\frac{\mathrm{4}}{\mathrm{3}},\mathrm{1}\right)}{\:\sqrt{\frac{\mathrm{26}}{\mathrm{9}}}}\:=\:\frac{\left(\mathrm{2},−\mathrm{8},\mathrm{6}\right)}{\:\sqrt{\mathrm{26}}} \\ $$
