
Question Number 115248 by aye48 last updated on 24/Sep/20

$$\mathrm{Express}\:\mathrm{cos}\:\mathrm{4x}\:\mathrm{interm}\:\mathrm{of}\:\mathrm{cos}\:\mathrm{x}. \\ $$
Answered by Olaf last updated on 24/Sep/20
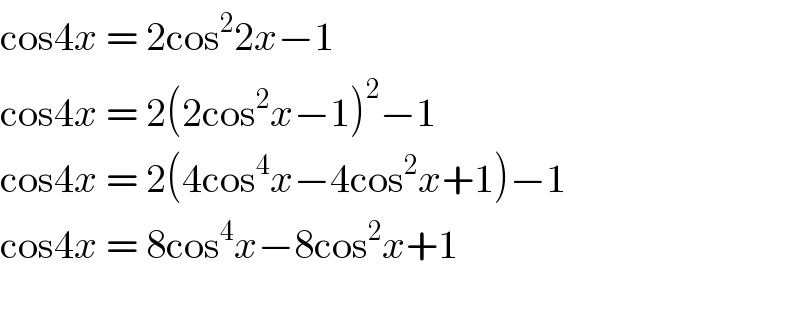
$$\mathrm{cos4}{x}\:=\:\mathrm{2cos}^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1} \\ $$$$\mathrm{cos4}{x}\:=\:\mathrm{2}\left(\mathrm{2cos}^{\mathrm{2}} {x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{cos4}{x}\:=\:\mathrm{2}\left(\mathrm{4cos}^{\mathrm{4}} {x}−\mathrm{4cos}^{\mathrm{2}} {x}+\mathrm{1}\right)−\mathrm{1} \\ $$$$\mathrm{cos4}{x}\:=\:\mathrm{8cos}^{\mathrm{4}} {x}−\mathrm{8cos}^{\mathrm{2}} {x}+\mathrm{1} \\ $$$$ \\ $$
