
Question Number 115238 by bemath last updated on 24/Sep/20
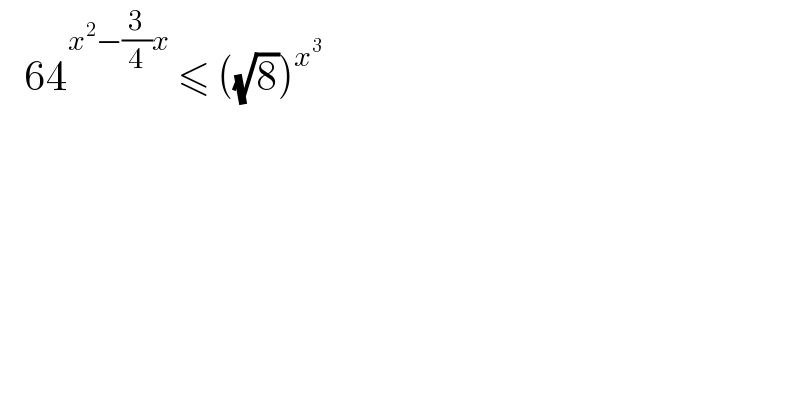
$$\:\:\:\mathrm{64}^{{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}} \:\leqslant\:\left(\sqrt{\mathrm{8}}\right)^{{x}^{\mathrm{3}} } \: \\ $$
Answered by Rasheed.Sindhi last updated on 24/Sep/20
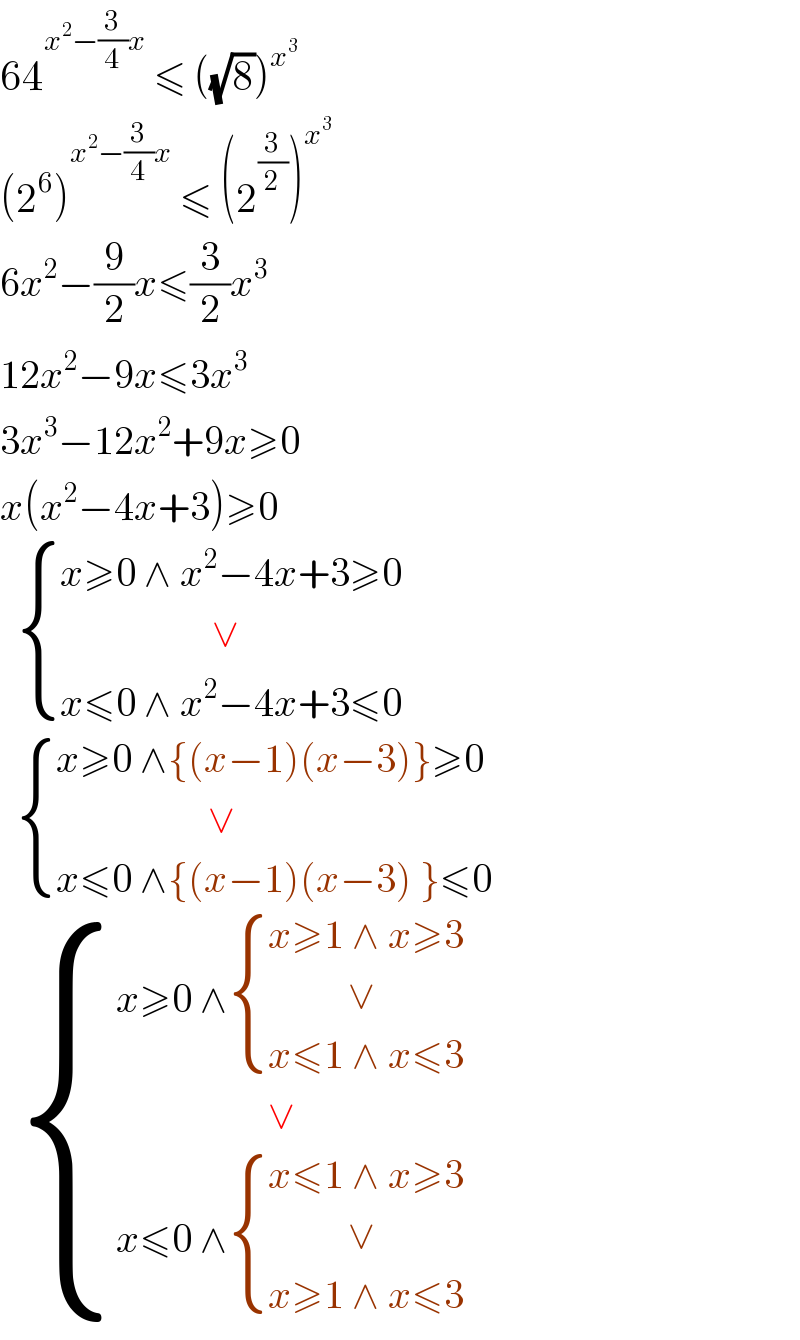
$$\mathrm{64}^{{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}} \:\leqslant\:\left(\sqrt{\mathrm{8}}\right)^{{x}^{\mathrm{3}} } \: \\ $$$$\left(\mathrm{2}^{\mathrm{6}} \right)^{{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}} \:\leqslant\:\left(\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)^{{x}^{\mathrm{3}} } \: \\ $$$$\mathrm{6}{x}^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{2}}{x}\leqslant\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{3}} \\ $$$$\mathrm{12}{x}^{\mathrm{2}} −\mathrm{9}{x}\leqslant\mathrm{3}{x}^{\mathrm{3}} \\ $$$$\mathrm{3}{x}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} +\mathrm{9}{x}\geqslant\mathrm{0} \\ $$$${x}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right)\geqslant\mathrm{0} \\ $$$$\:\:\begin{cases}{{x}\geqslant\mathrm{0}\:\wedge\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\geqslant\mathrm{0}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee}\\{{x}\leqslant\mathrm{0}\:\wedge\:{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\leqslant\mathrm{0}}\end{cases} \\ $$$$\:\:\begin{cases}{{x}\geqslant\mathrm{0}\:\wedge\left\{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)\right\}\geqslant\mathrm{0}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee}\\{{x}\leqslant\mathrm{0}\:\wedge\left\{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)\:\right\}\leqslant\mathrm{0}}\end{cases} \\ $$$$\:\:\begin{cases}{{x}\geqslant\mathrm{0}\:\wedge\begin{cases}{{x}\geqslant\mathrm{1}\:\wedge\:{x}\geqslant\mathrm{3}}\\{\:\:\:\:\:\:\:\:\:\:\vee}\\{{x}\leqslant\mathrm{1}\:\wedge\:{x}\leqslant\mathrm{3}}\end{cases}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\vee}\\{{x}\leqslant\mathrm{0}\:\wedge\begin{cases}{{x}\leqslant\mathrm{1}\:\wedge\:{x}\geqslant\mathrm{3}\:}\\{\:\:\:\:\:\:\:\:\:\:\vee}\\{{x}\geqslant\mathrm{1}\:\wedge\:{x}\leqslant\mathrm{3}}\end{cases}}\end{cases} \\ $$
Commented by bemath last updated on 24/Sep/20

$${gave}\:{kudos}\:{sir} \\ $$
Answered by Olaf last updated on 24/Sep/20
![x(x−1)(x−3) ≥ 0 (1) ⇔ x∈[0;1]∪[3;+∞[ Then (1) : x(x^2 −4x+3) ≥ 0 x^3 −4x^2 +3x ≥ 0 4x^2 −3x ≤ x^3 (3/2)(4x^2 −3x) ≤ (3/2)x^3 6(x^2 −(3/4)x) ≤ (3/2)x^3 6ln2(x^2 −(3/4)x) ≤ ((3/2)ln2)x^3 (x^2 −(3/4)x)ln64 ≤ x^3 ln(√8) ln64^(x^2 −(3/4)x) ≤ ln((√8))^x^3 64^(x^2 −(3/4)x) ≤( (√8))^x^3 S = [0;1]∪[3;+∞[](Q115243.png)
$${x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)\:\geqslant\:\mathrm{0}\:\left(\mathrm{1}\right) \\ $$$$\Leftrightarrow\:{x}\in\left[\mathrm{0};\mathrm{1}\right]\cup\left[\mathrm{3};+\infty\left[\right.\right. \\ $$$$\mathrm{Then}\:\left(\mathrm{1}\right)\::\:{x}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right)\:\geqslant\:\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{3}{x}\:\geqslant\:\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}\:\leqslant\:{x}^{\mathrm{3}} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}\right)\:\leqslant\:\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{3}} \\ $$$$\mathrm{6}\left({x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}\right)\:\leqslant\:\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{3}} \\ $$$$\mathrm{6ln2}\left({x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}\right)\:\leqslant\:\left(\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln2}\right){x}^{\mathrm{3}} \\ $$$$\left({x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}\right)\mathrm{ln64}\:\leqslant\:{x}^{\mathrm{3}} \mathrm{ln}\sqrt{\mathrm{8}} \\ $$$$\mathrm{ln64}^{{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}} \:\leqslant\:\mathrm{ln}\left(\sqrt{\mathrm{8}}\right)^{{x}^{\mathrm{3}} } \\ $$$$\mathrm{64}^{{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{x}} \:\leqslant\left(\:\sqrt{\mathrm{8}}\right)^{{x}^{\mathrm{3}} } \\ $$$$\mathscr{S}\:=\:\:\left[\mathrm{0};\mathrm{1}\right]\cup\left[\mathrm{3};+\infty\left[\right.\right. \\ $$$$ \\ $$
