
Question Number 115237 by nisaketto last updated on 24/Sep/20
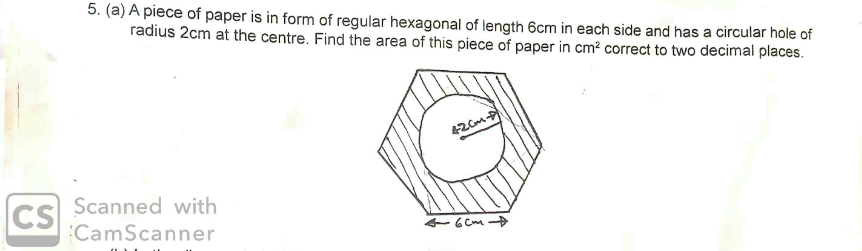
Answered by nimnim last updated on 24/Sep/20

$$\mathrm{A}=\mathrm{area}\:\mathrm{of}\:\mathrm{regular}\:\mathrm{hexagon}−\mathrm{area}\:\mathrm{of}\:\mathrm{circle} \\ $$$$\:\:\:\:=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{a}^{\mathrm{2}} −\pi\mathrm{r}^{\mathrm{2}} =\left(\frac{\mathrm{3}×\mathrm{1}.\mathrm{732}}{\mathrm{2}}×\mathrm{6}×\mathrm{6}\right)−\left(\frac{\mathrm{22}}{\mathrm{7}}×\mathrm{2}×\mathrm{2}\right) \\ $$$$\:\:\:\:=\mathrm{93}.\mathrm{528}−\mathrm{0}.\mathrm{785}=\mathrm{92}.\mathrm{77cm}^{\mathrm{2}} \\ $$$$\:\:{the}\:{question}\:{said}\:{radius}\:{is}\:\mathrm{2}{cm}\:{while}\:{the} \\ $$$$\:\:{figure}\:{represent}\:{radius}\:{is}\:\mathrm{4}.\mathrm{2}{cm} \\ $$$${OR}\:\left(\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}×\mathrm{6}×\mathrm{6}\right)−\left(\frac{\mathrm{22}}{\mathrm{7}}×\mathrm{4}.\mathrm{2}×\mathrm{4}.\mathrm{2}\right) \\ $$$$\:\:\:\:=\mathrm{93}.\mathrm{528}−\mathrm{55}.\mathrm{55} \\ $$$$\:\:\:\:=\mathrm{38}.\mathrm{088}\approx\mathrm{38}.\mathrm{09}\:\mathrm{cm}^{\mathrm{2}} \\ $$
Answered by EvoneAkashi last updated on 24/Sep/20
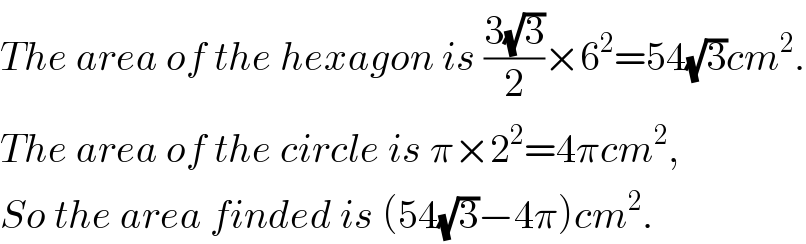
$${The}\:{area}\:{of}\:{the}\:{hexagon}\:{is}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}×\mathrm{6}^{\mathrm{2}} =\mathrm{54}\sqrt{\mathrm{3}}{cm}^{\mathrm{2}} . \\ $$$${The}\:{area}\:{of}\:{the}\:{circle}\:{is}\:\pi×\mathrm{2}^{\mathrm{2}} =\mathrm{4}\pi{cm}^{\mathrm{2}} , \\ $$$${So}\:{the}\:{area}\:{finded}\:{is}\:\left(\mathrm{54}\sqrt{\mathrm{3}}−\mathrm{4}\pi\right){cm}^{\mathrm{2}} . \\ $$
