
Question Number 115229 by mathdave last updated on 24/Sep/20
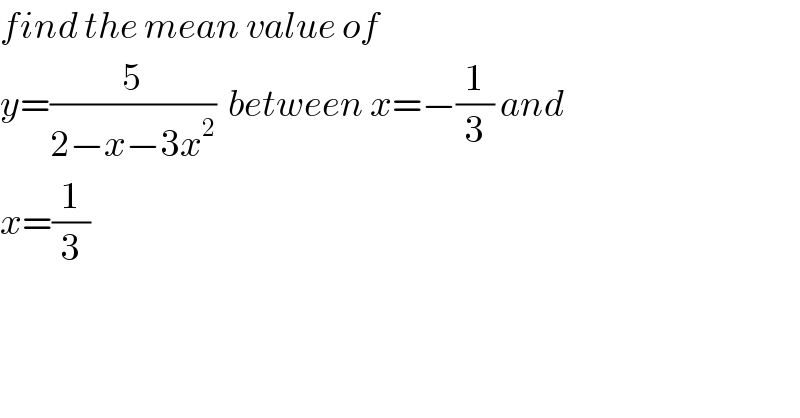
$${find}\:{the}\:{mean}\:{value}\:{of}\: \\ $$$${y}=\frac{\mathrm{5}}{\mathrm{2}−{x}−\mathrm{3}{x}^{\mathrm{2}} }\:\:{between}\:{x}=−\frac{\mathrm{1}}{\mathrm{3}}\:{and} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Answered by Olaf last updated on 24/Sep/20
![y^_ = (1/((1/3)−(−(1/3))))∫_(−(1/3)) ^(+(1/3)) (5/(2−x−3x^2 ))dx y^_ = −(5/2)∫_(−(1/3)) ^(+(1/3)) (1/(x^2 +(1/3)x−(2/3)))dx y^_ = −(5/2)∫_(−(1/3)) ^(+(1/3)) (1/((x+(1/6))^2 −((25)/(36))))dx y^_ = −(5/2)∫_(−(1/3)) ^(+(1/3)) (1/(((25)/(36))[((6/5)(x+(1/6)))^2 −1]))dx u = (1/5)(6x+1) y^_ = −3∫_(−(1/5)) ^(+(3/5)) (1/(u^2 −1))du y^_ = −3[(1/2)ln∣((u−1)/(u+1))∣]_(−(1/5)) ^(3/5) y^_ = −(3/2)[ln∣((−(2/5))/(8/5))∣−ln∣((−(6/5))/(4/5))∣] y^_ = −(3/2)[ln((1/4))−ln((3/2))] y^_ = −(3/2)ln((1/6)) y^_ = (3/2)ln6](Q115251.png)
$$ \\ $$$$\overset{\_} {{y}}\:=\:\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{3}}−\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)}\int_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{+\frac{\mathrm{1}}{\mathrm{3}}} \frac{\mathrm{5}}{\mathrm{2}−{x}−\mathrm{3}{x}^{\mathrm{2}} }{dx} \\ $$$$\overset{\_} {{y}}\:=\:−\frac{\mathrm{5}}{\mathrm{2}}\int_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{+\frac{\mathrm{1}}{\mathrm{3}}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}}{x}−\frac{\mathrm{2}}{\mathrm{3}}}{dx} \\ $$$$\overset{\_} {{y}}\:=\:−\frac{\mathrm{5}}{\mathrm{2}}\int_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{+\frac{\mathrm{1}}{\mathrm{3}}} \frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} −\frac{\mathrm{25}}{\mathrm{36}}}{dx} \\ $$$$\overset{\_} {{y}}\:=\:−\frac{\mathrm{5}}{\mathrm{2}}\int_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{+\frac{\mathrm{1}}{\mathrm{3}}} \frac{\mathrm{1}}{\frac{\mathrm{25}}{\mathrm{36}}\left[\left(\frac{\mathrm{6}}{\mathrm{5}}\left({x}+\frac{\mathrm{1}}{\mathrm{6}}\right)\right)^{\mathrm{2}} −\mathrm{1}\right]}{dx} \\ $$$${u}\:=\:\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{6}{x}+\mathrm{1}\right) \\ $$$$\overset{\_} {{y}}\:=\:−\mathrm{3}\int_{−\frac{\mathrm{1}}{\mathrm{5}}} ^{+\frac{\mathrm{3}}{\mathrm{5}}} \frac{\mathrm{1}}{{u}^{\mathrm{2}} −\mathrm{1}}{du} \\ $$$$\overset{\_} {{y}}\:=\:−\mathrm{3}\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\right]_{−\frac{\mathrm{1}}{\mathrm{5}}} ^{\frac{\mathrm{3}}{\mathrm{5}}} \\ $$$$\overset{\_} {{y}}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}\left[\mathrm{ln}\mid\frac{−\frac{\mathrm{2}}{\mathrm{5}}}{\frac{\mathrm{8}}{\mathrm{5}}}\mid−\mathrm{ln}\mid\frac{−\frac{\mathrm{6}}{\mathrm{5}}}{\frac{\mathrm{4}}{\mathrm{5}}}\mid\right] \\ $$$$\overset{\_} {{y}}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}\left[\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)−\mathrm{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right] \\ $$$$\overset{\_} {{y}}\:=\:−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{6}}\right) \\ $$$$\overset{\_} {{y}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln6} \\ $$
Commented by mathdave last updated on 24/Sep/20

$${gud}\:{work}\: \\ $$
Answered by Bird last updated on 24/Sep/20
![the mean value is (1/(b−a))∫_a ^b f(x)dx =(1/((1/3)−(−(1/3))))∫_(−(1/3)) ^(1/(3 )) (5/(−3x^2 −x+2))dx =−((15)/2) ∫_(−(1/3)) ^(1/3) (dx/(3x^2 +x−2)) Δ =1−4(−6) =25 ⇒x_1 =((−1+5)/6) =(2/3) and x_2 =((−1−5)/6) =−1 ⇒ M_f =−((15)/2) ∫_(−(1/3)) ^(1/3) (dx/(3(x−(2/3))(x+1))) =−(5/2)×(3/5) ∫_(−(1/3)) ^(1/3) ((1/(x−(2/3)))−(1/(x+1)))dx =−(3/2)[ln∣((x−(2/3))/(x+1))∣]_(−(1/3)) ^(1/3) =−(3/2){ln∣((−(1/3))/(4/3))∣−ln∣((−1)/(2/3))∣} =−(3/2){ln((3/4))−ln((3/2))} =−(3/2)ln((3/4)×(2/3)) =−(3/2)ln((1/2)) =((3ln(2))/2)](Q115295.png)
$${the}\:{mean}\:{value}\:{is}\:\frac{\mathrm{1}}{{b}−{a}}\int_{{a}} ^{{b}} {f}\left({x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{3}}−\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)}\int_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{3}\:}} \:\frac{\mathrm{5}}{−\mathrm{3}{x}^{\mathrm{2}} −{x}+\mathrm{2}}{dx} \\ $$$$=−\frac{\mathrm{15}}{\mathrm{2}}\:\int_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\frac{{dx}}{\mathrm{3}{x}^{\mathrm{2}} +{x}−\mathrm{2}} \\ $$$$\Delta\:=\mathrm{1}−\mathrm{4}\left(−\mathrm{6}\right)\:=\mathrm{25}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{5}}{\mathrm{6}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:{and}\:{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{5}}{\mathrm{6}}\:=−\mathrm{1}\:\Rightarrow \\ $$$${M}_{{f}} \:=−\frac{\mathrm{15}}{\mathrm{2}}\:\int_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\frac{{dx}}{\mathrm{3}\left({x}−\frac{\mathrm{2}}{\mathrm{3}}\right)\left({x}+\mathrm{1}\right)} \\ $$$$=−\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{5}}\:\int_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \:\left(\frac{\mathrm{1}}{{x}−\frac{\mathrm{2}}{\mathrm{3}}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right){dx} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\left[{ln}\mid\frac{{x}−\frac{\mathrm{2}}{\mathrm{3}}}{{x}+\mathrm{1}}\mid\right]_{−\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\left\{{ln}\mid\frac{−\frac{\mathrm{1}}{\mathrm{3}}}{\frac{\mathrm{4}}{\mathrm{3}}}\mid−{ln}\mid\frac{−\mathrm{1}}{\frac{\mathrm{2}}{\mathrm{3}}}\mid\right\} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\left\{{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)−{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right\} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{2}}{\mathrm{3}}\right)\:=−\frac{\mathrm{3}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{3}{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$ \\ $$
