
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 115170 by bobhans last updated on 24/Sep/20
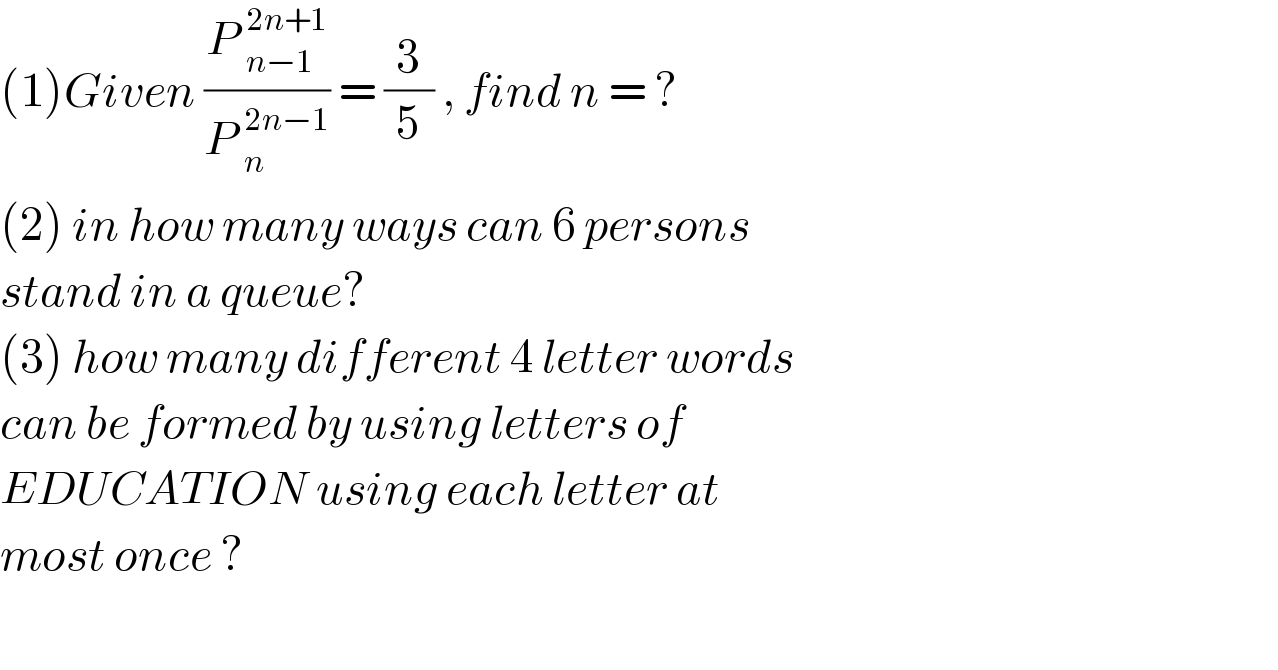
$$\left(\mathrm{1}\right){Given}\:\frac{{P}\:_{{n}−\mathrm{1}} ^{\mathrm{2}{n}+\mathrm{1}} }{{P}\:_{{n}} ^{\mathrm{2}{n}−\mathrm{1}} }\:=\:\frac{\mathrm{3}}{\mathrm{5}}\:,\:{find}\:{n}\:=\:? \\ $$$$\left(\mathrm{2}\right)\:{in}\:{how}\:{many}\:{ways}\:{can}\:\mathrm{6}\:{persons} \\ $$$${stand}\:{in}\:{a}\:{queue}? \\ $$$$\left(\mathrm{3}\right)\:{how}\:{many}\:{different}\:\mathrm{4}\:{letter}\:{words} \\ $$$${can}\:{be}\:{formed}\:{by}\:{using}\:{letters}\:{of}\: \\ $$$${EDUCATION}\:{using}\:{each}\:{letter}\:{at}\: \\ $$$${most}\:{once}\:? \\ $$$$ \\ $$
Answered by bemath last updated on 24/Sep/20
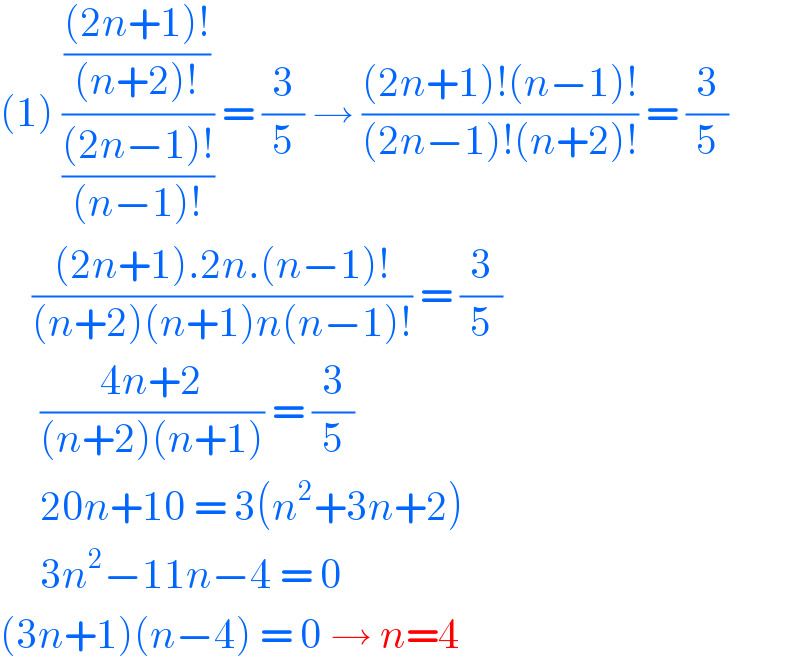
$$\left(\mathrm{1}\right)\:\frac{\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{\left({n}+\mathrm{2}\right)!}}{\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)!}{\left({n}−\mathrm{1}\right)!}}\:=\:\frac{\mathrm{3}}{\mathrm{5}}\:\rightarrow\:\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)!\left({n}−\mathrm{1}\right)!}{\left(\mathrm{2}{n}−\mathrm{1}\right)!\left({n}+\mathrm{2}\right)!}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\:\:\:\:\frac{\left(\mathrm{2}{n}+\mathrm{1}\right).\mathrm{2}{n}.\left({n}−\mathrm{1}\right)!}{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right){n}\left({n}−\mathrm{1}\right)!}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\frac{\mathrm{4}{n}+\mathrm{2}}{\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right)}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\:\:\:\:\:\mathrm{20}{n}+\mathrm{10}\:=\:\mathrm{3}\left({n}^{\mathrm{2}} +\mathrm{3}{n}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\mathrm{3}{n}^{\mathrm{2}} −\mathrm{11}{n}−\mathrm{4}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{3}{n}+\mathrm{1}\right)\left({n}−\mathrm{4}\right)\:=\:\mathrm{0}\:\rightarrow\:{n}=\mathrm{4} \\ $$
Answered by bemath last updated on 24/Sep/20
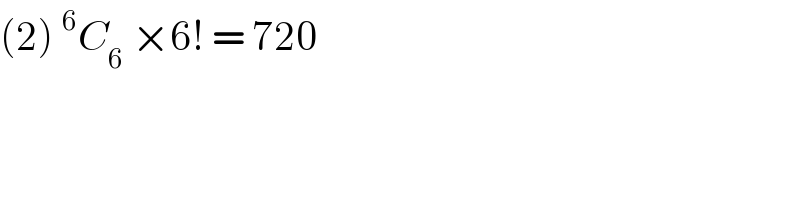
$$\left(\mathrm{2}\right)\:^{\mathrm{6}} {C}_{\mathrm{6}} \:×\mathrm{6}!\:=\:\mathrm{720} \\ $$
Answered by bemath last updated on 24/Sep/20
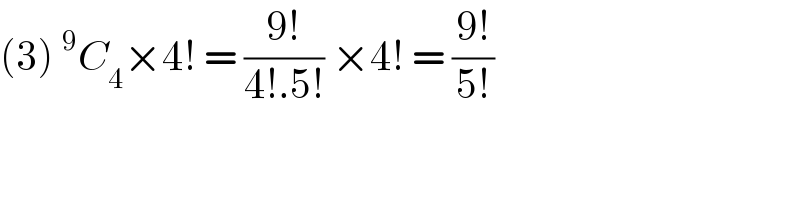
$$\left(\mathrm{3}\right)\:^{\mathrm{9}} {C}_{\mathrm{4}} ×\mathrm{4}!\:=\:\frac{\mathrm{9}!}{\mathrm{4}!.\mathrm{5}!}\:×\mathrm{4}!\:=\:\frac{\mathrm{9}!}{\mathrm{5}!} \\ $$
