
Question Number 115117 by bobhans last updated on 23/Sep/20
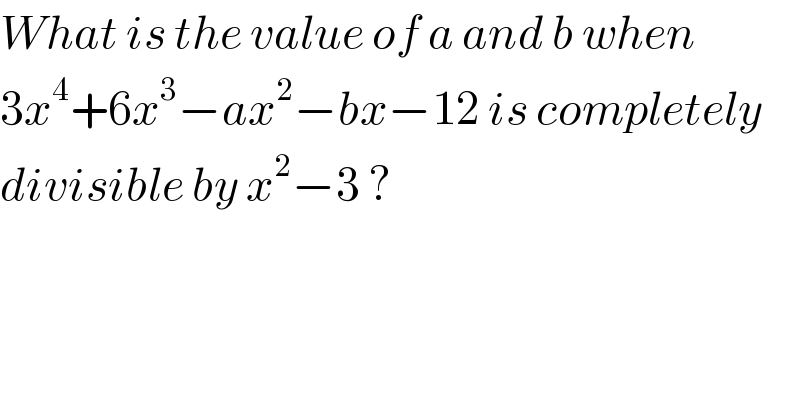
$${What}\:{is}\:{the}\:{value}\:{of}\:{a}\:{and}\:{b}\:{when}\: \\ $$$$\mathrm{3}{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{3}} −{ax}^{\mathrm{2}} −{bx}−\mathrm{12}\:{is}\:{completely} \\ $$$${divisible}\:{by}\:{x}^{\mathrm{2}} −\mathrm{3}\:? \\ $$
Answered by john santu last updated on 23/Sep/20

$${Write}\:{your}\:{polynomial}\:{as}\: \\ $$$${p}\left({x}\right)=\:{x}^{\mathrm{2}} \left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{6}{x}−{a}\right)−{bx}−\mathrm{12} \\ $$$${now}\:{computing}\:{the}\:{remainder}\:{of} \\ $$$${the}\:{division}\:{is}\:{easy}.\:{Substituting}\: \\ $$$$\mathrm{3}\:{for}\:{x}^{\mathrm{2}} \:\Rightarrow\:\mathrm{3}\left(\mathrm{3}.\mathrm{3}+\mathrm{6}{x}−{a}\right)−{bx}−\mathrm{12}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{3}\left(\mathrm{6}{x}+\mathrm{9}−{a}\right)−{bx}−\mathrm{12}\:=\:\mathrm{0}{x}\:+\:\mathrm{0} \\ $$$$\begin{cases}{\mathrm{18}−{b}=\mathrm{0}\rightarrow{b}=\mathrm{18}}\\{\mathrm{27}−\mathrm{3}{a}−\mathrm{12}=\mathrm{0}\rightarrow{a}=\:\mathrm{5}\:\:}\end{cases} \\ $$
