
Question Number 115051 by gab last updated on 23/Sep/20
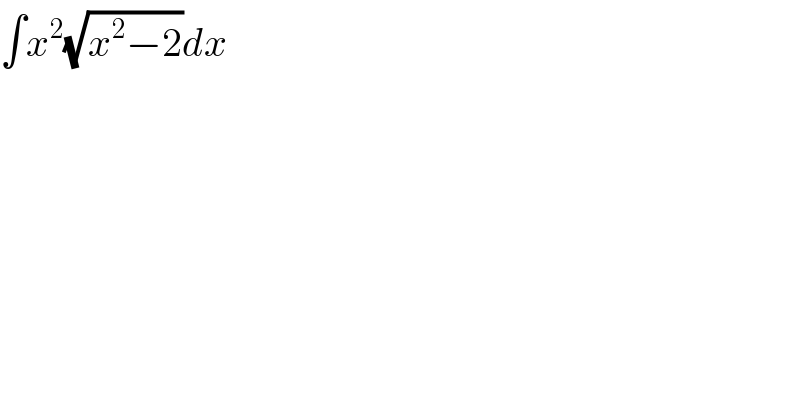
$$\int{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −\mathrm{2}}{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Sep/20
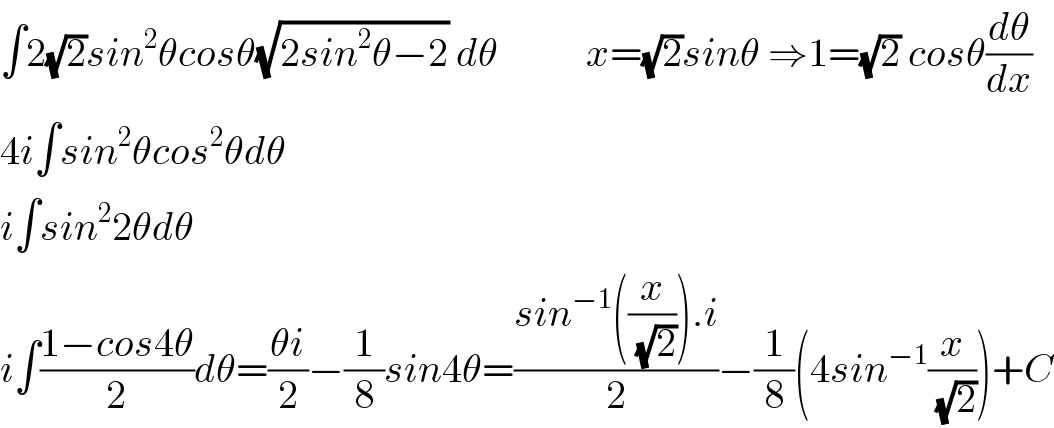
$$\int\mathrm{2}\sqrt{\mathrm{2}}{sin}^{\mathrm{2}} \theta{cos}\theta\sqrt{\mathrm{2}{sin}^{\mathrm{2}} \theta−\mathrm{2}}\:{d}\theta\:\:\:\:\:\:\:\:\:\:\:{x}=\sqrt{\mathrm{2}}{sin}\theta\:\Rightarrow\mathrm{1}=\sqrt{\mathrm{2}}\:{cos}\theta\frac{{d}\theta}{{dx}}\: \\ $$$$\mathrm{4}{i}\int{sin}^{\mathrm{2}} \theta{cos}^{\mathrm{2}} \theta{d}\theta \\ $$$${i}\int{sin}^{\mathrm{2}} \mathrm{2}\theta{d}\theta \\ $$$${i}\int\frac{\mathrm{1}−{cos}\mathrm{4}\theta}{\mathrm{2}}{d}\theta=\frac{\theta{i}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}{sin}\mathrm{4}\theta=\frac{{sin}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right).{i}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{4}{sin}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{\mathrm{2}}}\right)+{C} \\ $$
Commented by gab last updated on 23/Sep/20
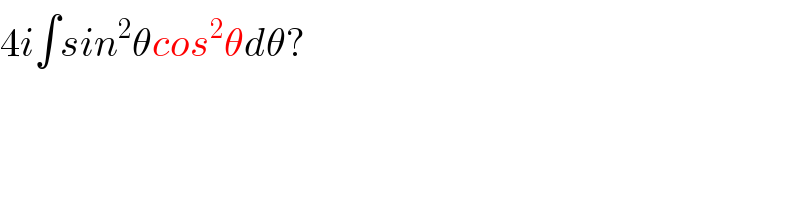
$$\mathrm{4}{i}\int{sin}^{\mathrm{2}} \theta{cos}^{\mathrm{2}} \theta{d}\theta? \\ $$
Commented by gab last updated on 23/Sep/20
$${sorry}...\:{i}\:{got}\:{it}...\:{thanks} \\ $$
Commented by mathmax by abdo last updated on 23/Sep/20

$$\mathrm{not}\:\mathrm{correct}! \\ $$
Commented by Dwaipayan Shikari last updated on 23/Sep/20
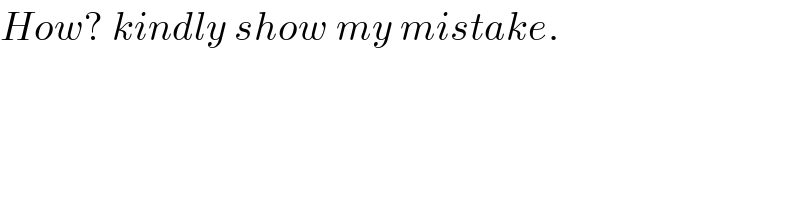
$${How}?\:{kindly}\:{show}\:{my}\:{mistake}. \\ $$
Commented by Bird last updated on 24/Sep/20
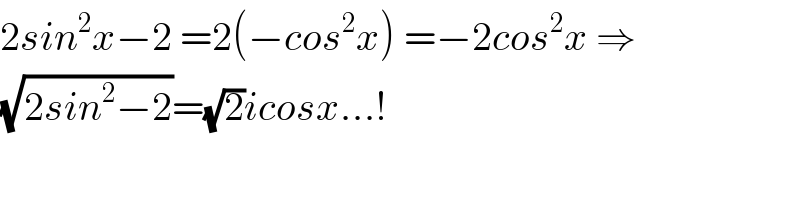
$$\mathrm{2}{sin}^{\mathrm{2}} {x}−\mathrm{2}\:=\mathrm{2}\left(−{cos}^{\mathrm{2}} {x}\right)\:=−\mathrm{2}{cos}^{\mathrm{2}} {x}\:\Rightarrow \\ $$$$\sqrt{\mathrm{2}{sin}^{\mathrm{2}} −\mathrm{2}}=\sqrt{\mathrm{2}}{icosx}...! \\ $$
Answered by mathmax by abdo last updated on 23/Sep/20
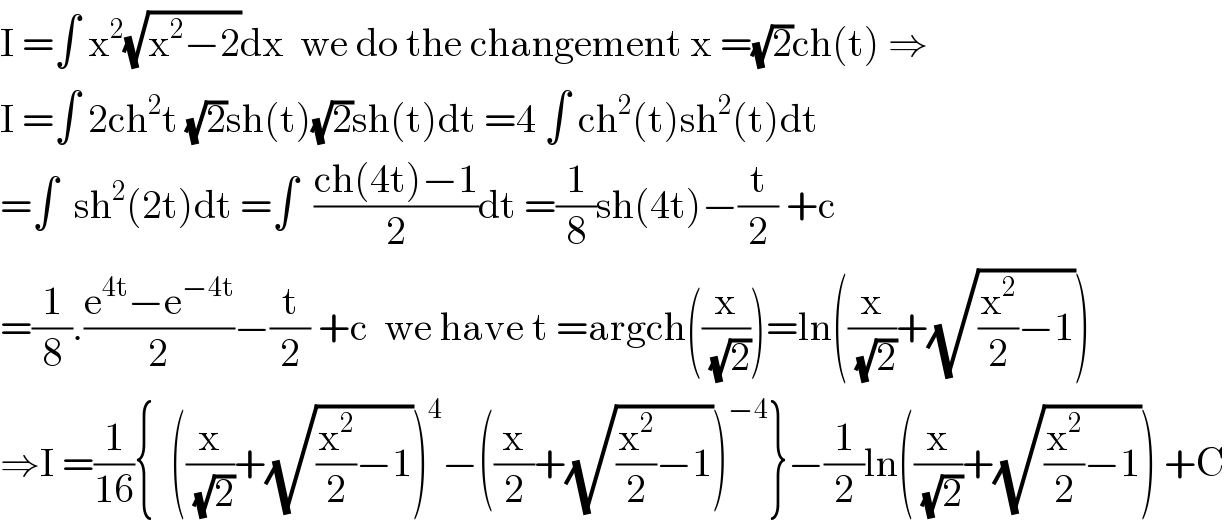
$$\mathrm{I}\:=\int\:\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}\:=\sqrt{\mathrm{2}}\mathrm{ch}\left(\mathrm{t}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\mathrm{2ch}^{\mathrm{2}} \mathrm{t}\:\sqrt{\mathrm{2}}\mathrm{sh}\left(\mathrm{t}\right)\sqrt{\mathrm{2}}\mathrm{sh}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{4}\:\int\:\mathrm{ch}^{\mathrm{2}} \left(\mathrm{t}\right)\mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\int\:\:\mathrm{sh}^{\mathrm{2}} \left(\mathrm{2t}\right)\mathrm{dt}\:=\int\:\:\frac{\mathrm{ch}\left(\mathrm{4t}\right)−\mathrm{1}}{\mathrm{2}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sh}\left(\mathrm{4t}\right)−\frac{\mathrm{t}}{\mathrm{2}}\:+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}.\frac{\mathrm{e}^{\mathrm{4t}} −\mathrm{e}^{−\mathrm{4t}} }{\mathrm{2}}−\frac{\mathrm{t}}{\mathrm{2}}\:+\mathrm{c}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{t}\:=\mathrm{argch}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{2}}}\right)=\mathrm{ln}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{2}}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$\Rightarrow\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{16}}\left\{\:\:\left(\frac{\mathrm{x}}{\sqrt{\mathrm{2}}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)^{\mathrm{4}} −\left(\frac{\mathrm{x}}{\mathrm{2}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)^{−\mathrm{4}} \right\}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{x}}{\sqrt{\mathrm{2}}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}\right)\:+\mathrm{C} \\ $$
Answered by 1549442205PVT last updated on 23/Sep/20
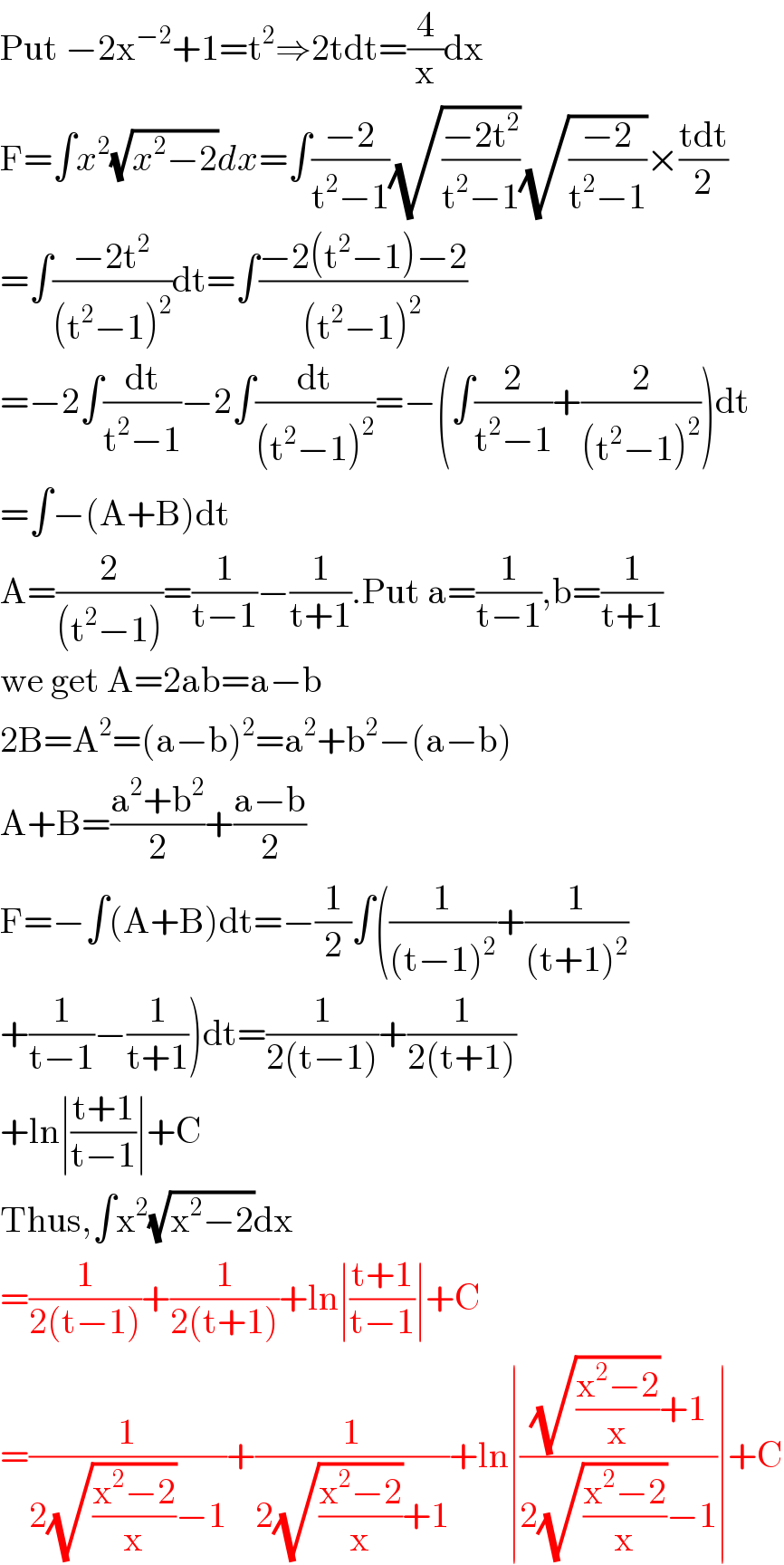
$$\mathrm{Put}\:−\mathrm{2x}^{−\mathrm{2}} +\mathrm{1}=\mathrm{t}^{\mathrm{2}} \Rightarrow\mathrm{2tdt}=\frac{\mathrm{4}}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{F}=\int{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} −\mathrm{2}}{dx}=\int\frac{−\mathrm{2}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\sqrt{\frac{−\mathrm{2t}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}}\sqrt{\frac{−\mathrm{2}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}}×\frac{\mathrm{tdt}}{\mathrm{2}} \\ $$$$=\int\frac{−\mathrm{2t}^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}=\int\frac{−\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\mathrm{2}\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}−\mathrm{2}\int\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }=−\left(\int\frac{\mathrm{2}}{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{2}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\right)\mathrm{dt} \\ $$$$=\int−\left(\mathrm{A}+\mathrm{B}\right)\mathrm{dt} \\ $$$$\mathrm{A}=\frac{\mathrm{2}}{\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}.\mathrm{Put}\:\mathrm{a}=\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}},\mathrm{b}=\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{A}=\mathrm{2ab}=\mathrm{a}−\mathrm{b} \\ $$$$\mathrm{2B}=\mathrm{A}^{\mathrm{2}} =\left(\mathrm{a}−\mathrm{b}\right)^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\left(\mathrm{a}−\mathrm{b}\right) \\ $$$$\mathrm{A}+\mathrm{B}=\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}} \\ $$$$\mathrm{F}=−\int\left(\mathrm{A}+\mathrm{B}\right)\mathrm{dt}=−\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }\right. \\ $$$$\left.+\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}}\right)\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{t}+\mathrm{1}\right)} \\ $$$$+\mathrm{ln}\mid\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\mid+\mathrm{C} \\ $$$$\mathrm{Thus},\int\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{t}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{t}+\mathrm{1}\right)}+\mathrm{ln}\mid\frac{\mathrm{t}+\mathrm{1}}{\mathrm{t}−\mathrm{1}}\mid+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}}}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}}}+\mathrm{1}}+\mathrm{ln}\mid\frac{\sqrt{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}}}+\mathrm{1}}{\mathrm{2}\sqrt{\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{x}}}−\mathrm{1}}\mid+\mathrm{C} \\ $$
