Question and Answers Forum

All Questions      Topic List

Coordinate Geometry Questions

Previous in All Question      Next in All Question      

Previous in Coordinate Geometry      Next in Coordinate Geometry      

Question Number 115035 by bobhans last updated on 23/Sep/20

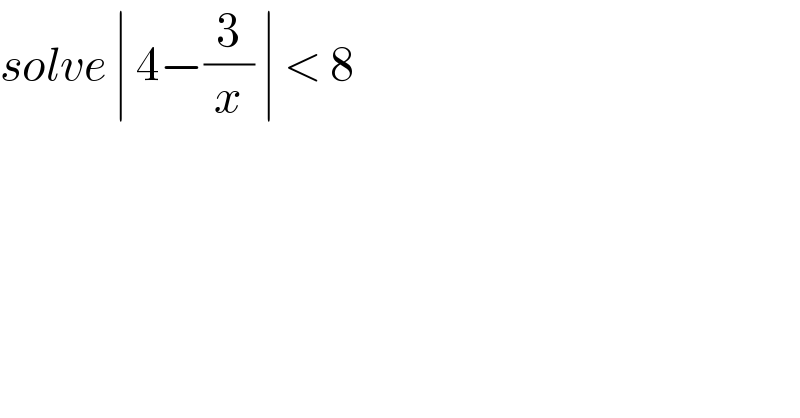
solve ∣ 4−(3/x) ∣ < 8

$${solve}\:\mid\:\mathrm{4}−\frac{\mathrm{3}}{{x}}\:\mid\:<\:\mathrm{8} \\ $$

Commented bybemath last updated on 23/Sep/20

⇔ −8 < 4−(3/x) < 8 case(1) → −8 < 4−(3/x) (3/x) < 12 ; (1/x) < 4 ; ((1−4x)/x) < 0 ((4x−1)/x) > 0 ; x < 0 ∪ x > (1/4) case(2) 4−(3/x) < 8 ; −(3/x) < 4 (3/x) > −4 ; ((3+4x)/x) > 0 x < −(3/4) ∪ x > 0 solution set is (−∞, −(3/4)) ∪((1/4), ∞)

$$\Leftrightarrow\:−\mathrm{8}\:<\:\mathrm{4}−\frac{\mathrm{3}}{{x}}\:<\:\mathrm{8} \\ $$ $${case}\left(\mathrm{1}\right)\:\rightarrow\:−\mathrm{8}\:<\:\mathrm{4}−\frac{\mathrm{3}}{{x}} \\ $$ $$\:\:\:\:\:\frac{\mathrm{3}}{{x}}\:<\:\mathrm{12}\:;\:\frac{\mathrm{1}}{{x}}\:<\:\mathrm{4}\:;\:\frac{\mathrm{1}−\mathrm{4}{x}}{{x}}\:<\:\mathrm{0} \\ $$ $$\:\:\:\:\:\:\frac{\mathrm{4}{x}−\mathrm{1}}{{x}}\:>\:\mathrm{0}\:;\:{x}\:<\:\mathrm{0}\:\cup\:{x}\:>\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$ $${case}\left(\mathrm{2}\right)\:\mathrm{4}−\frac{\mathrm{3}}{{x}}\:<\:\mathrm{8}\:;\:−\frac{\mathrm{3}}{{x}}\:<\:\mathrm{4} \\ $$ $$\:\:\frac{\mathrm{3}}{{x}}\:>\:−\mathrm{4}\:;\:\frac{\mathrm{3}+\mathrm{4}{x}}{{x}}\:>\:\mathrm{0} \\ $$ $$\:\:{x}\:<\:−\frac{\mathrm{3}}{\mathrm{4}}\:\cup\:{x}\:>\:\mathrm{0} \\ $$ $${solution}\:{set}\:{is}\:\left(−\infty,\:−\frac{\mathrm{3}}{\mathrm{4}}\right)\:\cup\left(\frac{\mathrm{1}}{\mathrm{4}},\:\infty\right) \\ $$

Commented bybobhans last updated on 23/Sep/20

santuyy

$${santuyy} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com