
Question Number 114988 by ZiYangLee last updated on 22/Sep/20
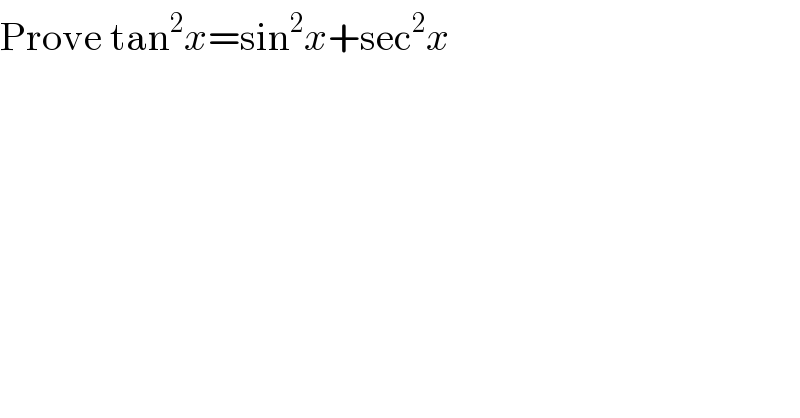
$$\mathrm{Prove}\:\mathrm{tan}^{\mathrm{2}} {x}=\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{sec}^{\mathrm{2}} {x} \\ $$
Answered by Olaf last updated on 22/Sep/20
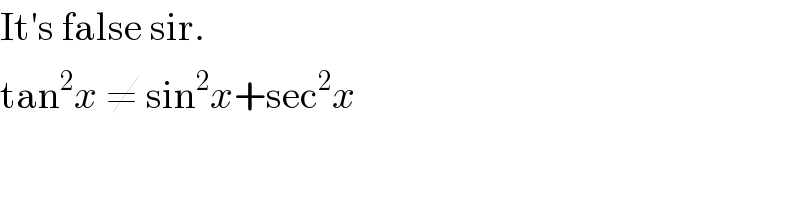
$$\mathrm{It}'\mathrm{s}\:\mathrm{false}\:\mathrm{sir}. \\ $$$$\mathrm{tan}^{\mathrm{2}} {x}\:\neq\:\mathrm{sin}^{\mathrm{2}} {x}+\mathrm{sec}^{\mathrm{2}} {x} \\ $$
Commented by ZiYangLee last updated on 22/Sep/20

$$\mathrm{Ok}\:\mathrm{sir}\:\mathrm{tks} \\ $$
Answered by Olaf last updated on 22/Sep/20
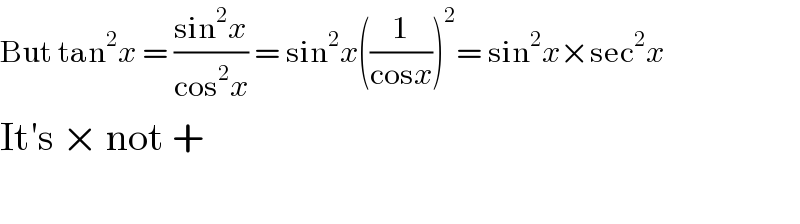
$$\mathrm{But}\:\mathrm{tan}^{\mathrm{2}} {x}\:=\:\frac{\mathrm{sin}^{\mathrm{2}} {x}}{\mathrm{cos}^{\mathrm{2}} {x}}\:=\:\mathrm{sin}^{\mathrm{2}} {x}\left(\frac{\mathrm{1}}{\mathrm{cos}{x}}\right)^{\mathrm{2}} =\:\mathrm{sin}^{\mathrm{2}} {x}×\mathrm{sec}^{\mathrm{2}} {x} \\ $$$$\mathrm{It}'\mathrm{s}\:×\:\mathrm{not}\:+ \\ $$$$ \\ $$
