
Question Number 114975 by mnjuly1970 last updated on 22/Sep/20
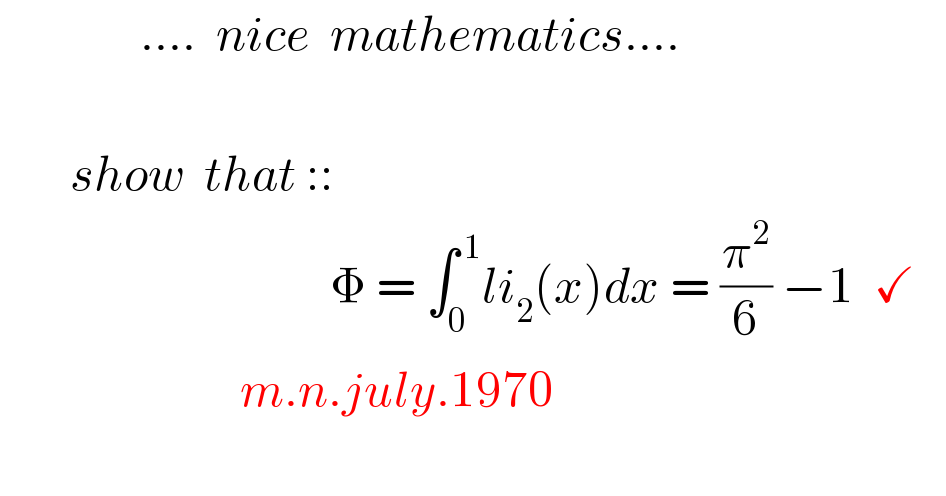
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:....\:\:{nice}\:\:{mathematics}....\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:{show}\:\:{that}\:::\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {li}_{\mathrm{2}} \left({x}\right){dx}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\mathrm{1}\:\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}.{n}.{july}.\mathrm{1970} \\ $$$$ \\ $$
Answered by maths mind last updated on 24/Sep/20

$${li}_{\mathrm{2}} \left({x}\right)=\Sigma\frac{{x}^{{n}} }{{n}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {li}_{\mathrm{2}} \left({x}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} }{{n}^{\mathrm{2}} }{dx}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right){n}^{\mathrm{2}} } \\ $$$$=\Sigma\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}}\right) \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1} \\ $$
