
Question Number 114965 by joki last updated on 22/Sep/20
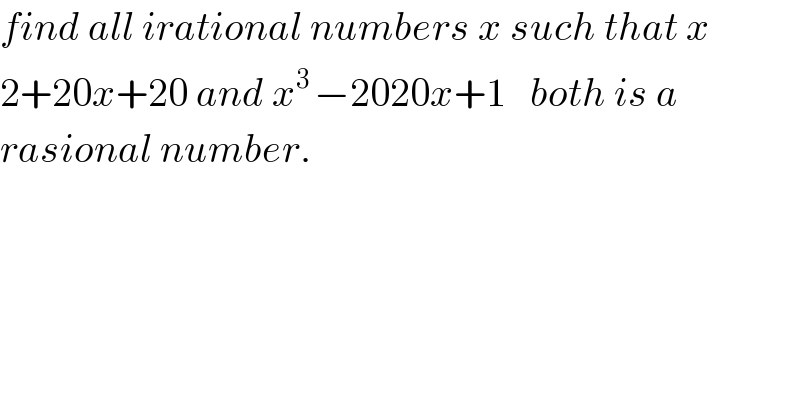
$${find}\:{all}\:{irational}\:{numbers}\:{x}\:{such}\:{that}\:{x} \\ $$$$\mathrm{2}+\mathrm{20}{x}+\mathrm{20}\:{and}\:{x}^{\mathrm{3}\:} −\mathrm{2020}{x}+\mathrm{1}\:\:\:{both}\:{is}\:{a} \\ $$$${rasional}\:{number}. \\ $$
Answered by MJS_new last updated on 22/Sep/20
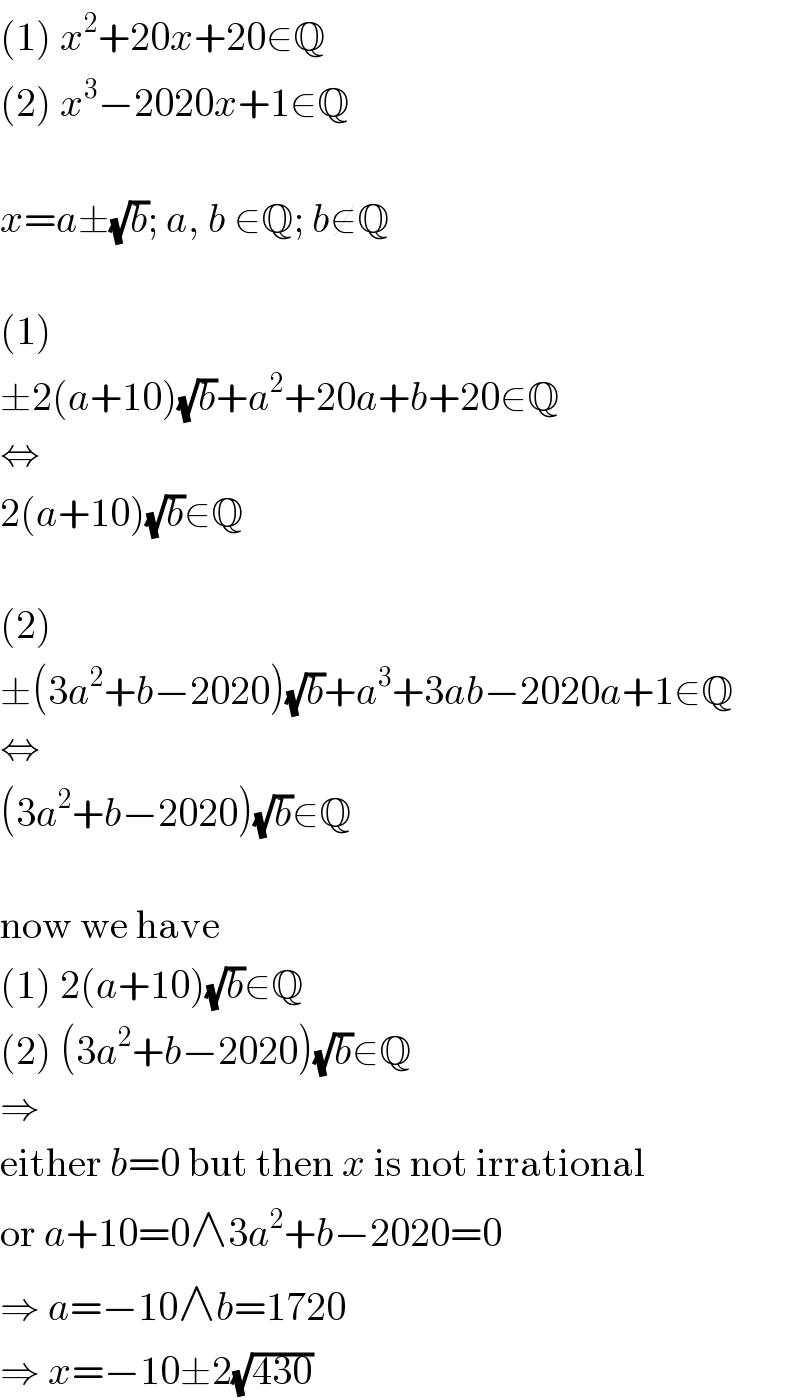
$$\left(\mathrm{1}\right)\:{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{20}\in\mathbb{Q} \\ $$$$\left(\mathrm{2}\right)\:{x}^{\mathrm{3}} −\mathrm{2020}{x}+\mathrm{1}\in\mathbb{Q} \\ $$$$ \\ $$$${x}={a}\pm\sqrt{{b}};\:{a},\:{b}\:\in\mathbb{Q};\:{b}\notin\mathbb{Q} \\ $$$$ \\ $$$$\left(\mathrm{1}\right) \\ $$$$\pm\mathrm{2}\left({a}+\mathrm{10}\right)\sqrt{{b}}+{a}^{\mathrm{2}} +\mathrm{20}{a}+{b}+\mathrm{20}\in\mathbb{Q} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{2}\left({a}+\mathrm{10}\right)\sqrt{{b}}\in\mathbb{Q} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$\pm\left(\mathrm{3}{a}^{\mathrm{2}} +{b}−\mathrm{2020}\right)\sqrt{{b}}+{a}^{\mathrm{3}} +\mathrm{3}{ab}−\mathrm{2020}{a}+\mathrm{1}\in\mathbb{Q} \\ $$$$\Leftrightarrow \\ $$$$\left(\mathrm{3}{a}^{\mathrm{2}} +{b}−\mathrm{2020}\right)\sqrt{{b}}\in\mathbb{Q} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}\left({a}+\mathrm{10}\right)\sqrt{{b}}\in\mathbb{Q} \\ $$$$\left(\mathrm{2}\right)\:\left(\mathrm{3}{a}^{\mathrm{2}} +{b}−\mathrm{2020}\right)\sqrt{{b}}\in\mathbb{Q} \\ $$$$\Rightarrow \\ $$$$\mathrm{either}\:{b}=\mathrm{0}\:\mathrm{but}\:\mathrm{then}\:{x}\:\mathrm{is}\:\mathrm{not}\:\mathrm{irrational} \\ $$$$\mathrm{or}\:{a}+\mathrm{10}=\mathrm{0}\wedge\mathrm{3}{a}^{\mathrm{2}} +{b}−\mathrm{2020}=\mathrm{0} \\ $$$$\Rightarrow\:{a}=−\mathrm{10}\wedge{b}=\mathrm{1720} \\ $$$$\Rightarrow\:{x}=−\mathrm{10}\pm\mathrm{2}\sqrt{\mathrm{430}} \\ $$
