
Previous in Relation and Functions Next in Relation and Functions
Question Number 114878 by bobhans last updated on 21/Sep/20
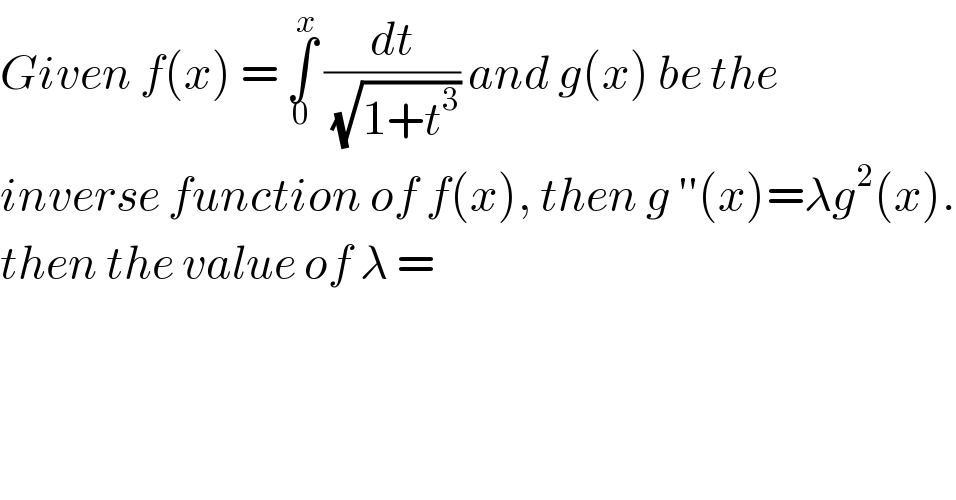
$${Given}\:{f}\left({x}\right)\:=\:\underset{\mathrm{0}} {\overset{{x}} {\int}}\:\frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{3}} }}\:{and}\:{g}\left({x}\right)\:{be}\:{the} \\ $$$${inverse}\:{function}\:{of}\:{f}\left({x}\right),\:{then}\:{g}\:''\left({x}\right)=\lambda{g}^{\mathrm{2}} \left({x}\right). \\ $$$${then}\:{the}\:{value}\:{of}\:\lambda\:= \\ $$
Answered by Olaf last updated on 21/Sep/20
![gof(x) = x f′(x)×g′of(x) = 1 g′of(x) = (1/(f′(x))) = (√(1+x^3 )) f′(x)×g′′of(x) = ((3x^2 )/(2(√(1+x^3 )))) g′′of(x) = (1/(f′(x)))[((3x^2 )/(2(√(1+x^3 ))))] g′′of(x) = (√(1+x^3 ))[((3x^2 )/(2(√(1+x^3 ))))] g′′of(x) = (3/2)x^2 g′′of(x) = (3/2)[gof(x)]^2 Let y = f(x) g′′(y) = (3/2)g^2 (y) g′′(y) = λg^2 (y) with λ = (3/2)](Q114903.png)
$${g}\mathrm{o}{f}\left({x}\right)\:=\:{x} \\ $$$${f}'\left({x}\right)×{g}'\mathrm{o}{f}\left({x}\right)\:=\:\mathrm{1} \\ $$$${g}'\mathrm{o}{f}\left({x}\right)\:=\:\frac{\mathrm{1}}{{f}'\left({x}\right)}\:=\:\sqrt{\mathrm{1}+{x}^{\mathrm{3}} } \\ $$$${f}'\left({x}\right)×{g}''\mathrm{o}{f}\left({x}\right)\:=\:\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }} \\ $$$${g}''\mathrm{o}{f}\left({x}\right)\:=\:\frac{\mathrm{1}}{{f}'\left({x}\right)}\left[\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }}\right] \\ $$$${g}''\mathrm{o}{f}\left({x}\right)\:=\:\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }\left[\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{3}} }}\right] \\ $$$${g}''\mathrm{o}{f}\left({x}\right)\:=\:\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \\ $$$${g}''\mathrm{o}{f}\left({x}\right)\:=\:\frac{\mathrm{3}}{\mathrm{2}}\left[{g}\mathrm{o}{f}\left({x}\right)\right]^{\mathrm{2}} \\ $$$$\mathrm{Let}\:{y}\:=\:{f}\left({x}\right) \\ $$$${g}''\left({y}\right)\:=\:\frac{\mathrm{3}}{\mathrm{2}}{g}^{\mathrm{2}} \left({y}\right) \\ $$$${g}''\left({y}\right)\:=\:\lambda{g}^{\mathrm{2}} \left({y}\right)\:\mathrm{with}\:\lambda\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by PRITHWISH SEN 2 last updated on 21/Sep/20
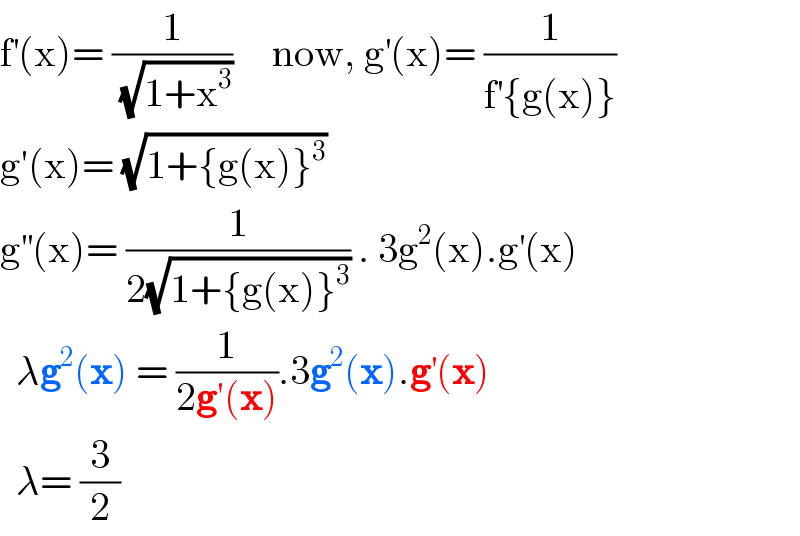
$$\mathrm{f}^{'} \left(\mathrm{x}\right)=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }}\:\:\:\:\:\mathrm{now},\:\mathrm{g}^{'} \left(\mathrm{x}\right)=\:\frac{\mathrm{1}}{\mathrm{f}^{'} \left\{\mathrm{g}\left(\mathrm{x}\right)\right\}} \\ $$$$\mathrm{g}'\left(\mathrm{x}\right)=\:\sqrt{\mathrm{1}+\left\{\mathrm{g}\left(\mathrm{x}\right)\right\}^{\mathrm{3}} } \\ $$$$\mathrm{g}^{''} \left(\mathrm{x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+\left\{\mathrm{g}\left(\mathrm{x}\right)\right\}^{\mathrm{3}} }}\:.\:\mathrm{3g}^{\mathrm{2}} \left(\mathrm{x}\right).\mathrm{g}^{'} \left(\mathrm{x}\right) \\ $$$$\:\:\lambda\boldsymbol{\mathrm{g}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mathrm{g}}'\left(\boldsymbol{\mathrm{x}}\right)}.\mathrm{3}\boldsymbol{\mathrm{g}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right).\boldsymbol{\mathrm{g}}^{'} \left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\:\:\lambda=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$
