
Question Number 114840 by zakirullah last updated on 21/Sep/20
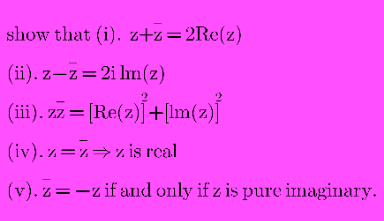
Answered by Aziztisffola last updated on 21/Sep/20
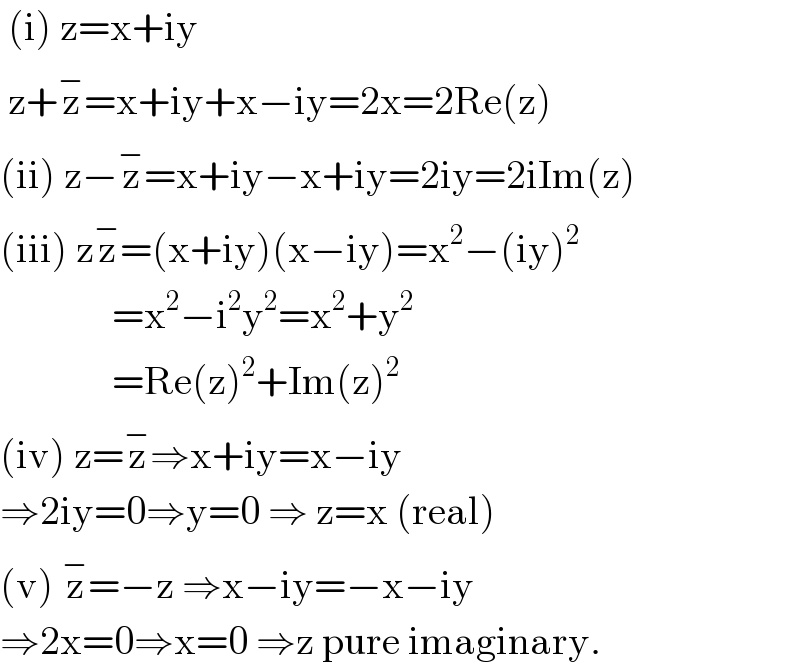
$$\:\left(\mathrm{i}\right)\:\mathrm{z}=\mathrm{x}+\mathrm{iy} \\ $$$$\:\mathrm{z}+\overset{−} {\mathrm{z}}=\mathrm{x}+\mathrm{iy}+\mathrm{x}−\mathrm{iy}=\mathrm{2x}=\mathrm{2Re}\left(\mathrm{z}\right) \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{z}−\overset{−} {\mathrm{z}}=\mathrm{x}+\mathrm{iy}−\mathrm{x}+\mathrm{iy}=\mathrm{2iy}=\mathrm{2iIm}\left(\mathrm{z}\right) \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{z}\overset{−} {\mathrm{z}}=\left(\mathrm{x}+\mathrm{iy}\right)\left(\mathrm{x}−\mathrm{iy}\right)=\mathrm{x}^{\mathrm{2}} −\left(\mathrm{iy}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{x}^{\mathrm{2}} −\mathrm{i}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} =\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{Re}\left(\mathrm{z}\right)^{\mathrm{2}} +\mathrm{Im}\left(\mathrm{z}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{iv}\right)\:\mathrm{z}=\overset{−} {\mathrm{z}}\Rightarrow\mathrm{x}+\mathrm{iy}=\mathrm{x}−\mathrm{iy} \\ $$$$\Rightarrow\mathrm{2iy}=\mathrm{0}\Rightarrow\mathrm{y}=\mathrm{0}\:\Rightarrow\:\mathrm{z}=\mathrm{x}\:\left(\mathrm{real}\right) \\ $$$$\left(\mathrm{v}\right)\:\overset{−} {\mathrm{z}}=−\mathrm{z}\:\Rightarrow\mathrm{x}−\mathrm{iy}=−\mathrm{x}−\mathrm{iy} \\ $$$$\Rightarrow\mathrm{2x}=\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{0}\:\Rightarrow\mathrm{z}\:\mathrm{pure}\:\mathrm{imaginary}. \\ $$
Commented by zakirullah last updated on 21/Sep/20

$$\boldsymbol{\mathrm{Sir}}\:\boldsymbol{\mathrm{alot}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{thanks}}. \\ $$
