
Question Number 114809 by bemath last updated on 21/Sep/20
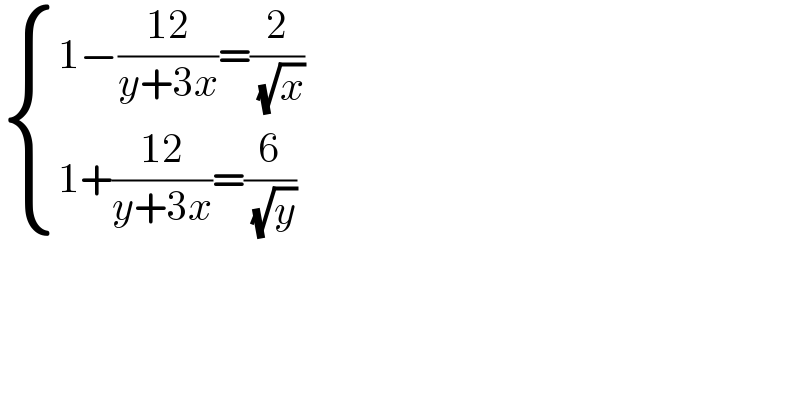
$$\begin{cases}{\mathrm{1}−\frac{\mathrm{12}}{{y}+\mathrm{3}{x}}=\frac{\mathrm{2}}{\:\sqrt{{x}}}}\\{\mathrm{1}+\frac{\mathrm{12}}{{y}+\mathrm{3}{x}}=\frac{\mathrm{6}}{\:\sqrt{{y}}}}\end{cases} \\ $$
Commented by bemath last updated on 21/Sep/20

$${set}\:\sqrt{{x}}\:=\:{u}\:\wedge\:\sqrt{{y}}\:=\:{v} \\ $$$$\Leftrightarrow\:\frac{\mathrm{12}}{{y}+\mathrm{3}{x}}\:=\:\frac{\mathrm{12}}{{y}+\mathrm{3}{x}}\:\Rightarrow\mathrm{1}−\frac{\mathrm{2}}{{u}}=\frac{\mathrm{6}}{{v}}−\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{1}\:=\:\frac{\mathrm{1}}{{u}}+\frac{\mathrm{3}}{{v}};\:\mathrm{3}{u}+{v}\:=\:{uv} \\ $$$$\Leftrightarrow\mathrm{1}−\frac{\mathrm{2}}{{u}}\:=\:\frac{\mathrm{12}}{{v}^{\mathrm{2}} +\mathrm{3}{u}^{\mathrm{2}} }\: \\ $$$$\Rightarrow\:\frac{{u}−\mathrm{2}}{{u}}\:=\:\frac{\mathrm{12}}{{v}^{\mathrm{2}} +\mathrm{3}{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{12}{u}\:=\:\left({u}−\mathrm{2}\right)\left(\mathrm{3}{u}^{\mathrm{2}} +{v}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{12}{u}\:=\:\mathrm{3}{u}^{\mathrm{3}} +{uv}.{v}−\mathrm{6}{u}^{\mathrm{2}} −\mathrm{2}{v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{12}{u}=\mathrm{3}{u}^{\mathrm{3}} +{v}\left(\mathrm{3}{u}+{v}\right)−\mathrm{6}{u}^{\mathrm{2}} −\mathrm{2}{v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{12}{u}=\mathrm{3}{u}^{\mathrm{3}} +\mathrm{3}{uv}−\mathrm{6}{u}^{\mathrm{2}} −{v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{12}{u}=\mathrm{3}{u}^{\mathrm{3}} +\mathrm{3}\left(\mathrm{3}{u}+{v}\right)−\mathrm{6}{u}^{\mathrm{2}} −{v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{12}{u}=\mathrm{3}{u}^{\mathrm{3}} +\mathrm{9}{u}+\mathrm{3}{v}−\mathrm{6}{u}^{\mathrm{2}} −{v}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{3}{u}^{\mathrm{3}} −\mathrm{6}{u}^{\mathrm{2}} −\mathrm{3}{u}+\mathrm{3}{v}−{v}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}{u}\left({u}^{\mathrm{2}} −\mathrm{2}{u}−\mathrm{1}\right)+\mathrm{3}{v}−{v}^{\mathrm{2}} =\mathrm{0} \\ $$
Answered by MJS_new last updated on 21/Sep/20
![let x=p^2 ∧y=q^2 p^2 with p,q >0 ⇒ { ((1−((12)/(p^2 q^2 +3p^2 ))=(2/p))),((1+((12)/(p^2 q^2 +3p^2 ))=(6/(pq)))) :} ⇒ { (((q^2 +3)p^2 −2(q^2 +3)p−12=0)),((q(q^2 +3)p^2 −6(q^2 +3)p+12q=0)) :} (2)−q×(1) 2(q−3)(q^2 +3)p+24q=0 p=−((12q)/((q−3)(q^2 +3))) insert into (1) [or (2)] and transform [q>0] ⇒ q^4 +6q^2 −27=0 ⇒ q=(√3) ⇒ p=1+(√3) ⇒ x=4+2(√3)∧y=12+6(√3)](Q114835.png)
$$\mathrm{let}\:{x}={p}^{\mathrm{2}} \wedge{y}={q}^{\mathrm{2}} {p}^{\mathrm{2}} \:\mathrm{with}\:{p},{q}\:>\mathrm{0} \\ $$$$\Rightarrow\:\begin{cases}{\mathrm{1}−\frac{\mathrm{12}}{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{3}{p}^{\mathrm{2}} }=\frac{\mathrm{2}}{{p}}}\\{\mathrm{1}+\frac{\mathrm{12}}{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +\mathrm{3}{p}^{\mathrm{2}} }=\frac{\mathrm{6}}{{pq}}}\end{cases} \\ $$$$\Rightarrow\:\begin{cases}{\left({q}^{\mathrm{2}} +\mathrm{3}\right){p}^{\mathrm{2}} −\mathrm{2}\left({q}^{\mathrm{2}} +\mathrm{3}\right){p}−\mathrm{12}=\mathrm{0}}\\{{q}\left({q}^{\mathrm{2}} +\mathrm{3}\right){p}^{\mathrm{2}} −\mathrm{6}\left({q}^{\mathrm{2}} +\mathrm{3}\right){p}+\mathrm{12}{q}=\mathrm{0}}\end{cases} \\ $$$$\left(\mathrm{2}\right)−{q}×\left(\mathrm{1}\right) \\ $$$$\mathrm{2}\left({q}−\mathrm{3}\right)\left({q}^{\mathrm{2}} +\mathrm{3}\right){p}+\mathrm{24}{q}=\mathrm{0} \\ $$$${p}=−\frac{\mathrm{12}{q}}{\left({q}−\mathrm{3}\right)\left({q}^{\mathrm{2}} +\mathrm{3}\right)} \\ $$$$\mathrm{insert}\:\mathrm{into}\:\left(\mathrm{1}\right)\:\left[\mathrm{or}\:\left(\mathrm{2}\right)\right]\:\mathrm{and}\:\mathrm{transform}\:\left[{q}>\mathrm{0}\right] \\ $$$$\Rightarrow\:{q}^{\mathrm{4}} +\mathrm{6}{q}^{\mathrm{2}} −\mathrm{27}=\mathrm{0} \\ $$$$\Rightarrow\:{q}=\sqrt{\mathrm{3}}\:\Rightarrow\:{p}=\mathrm{1}+\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:{x}=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\wedge{y}=\mathrm{12}+\mathrm{6}\sqrt{\mathrm{3}} \\ $$
Commented by bemath last updated on 21/Sep/20
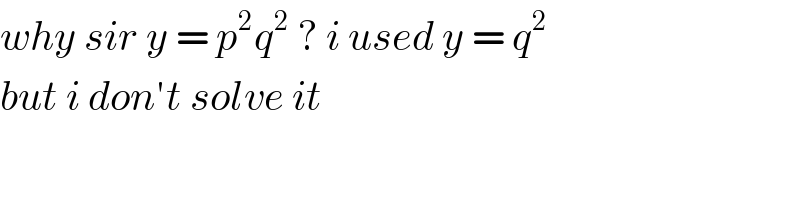
$${why}\:{sir}\:{y}\:=\:{p}^{\mathrm{2}} {q}^{\mathrm{2}} \:?\:{i}\:{used}\:{y}\:=\:{q}^{\mathrm{2}} \\ $$$${but}\:{i}\:{don}'{t}\:{solve}\:{it} \\ $$
Commented by MJS_new last updated on 21/Sep/20
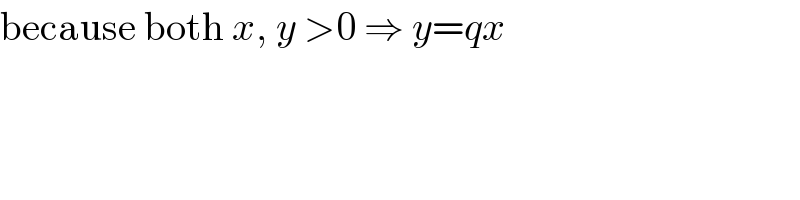
$$\mathrm{because}\:\mathrm{both}\:{x},\:{y}\:>\mathrm{0}\:\Rightarrow\:{y}={qx} \\ $$
Commented by bemath last updated on 21/Sep/20

$${gave}\:{kudos}\:{sir}. \\ $$
