
Question Number 114807 by Eric002 last updated on 21/Sep/20

$${is}\:{zero}\:{a}\:{natural}\:{number}\:\mathrm{0}\in\mathbb{N}? \\ $$
Commented by MJS_new last updated on 21/Sep/20

$$\mathrm{there}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{be}\:\mathrm{two}\:\mathrm{different}\:\mathrm{definitions} \\ $$$$\mathrm{of}\:\mathbb{N},\:\mathrm{both}\:\mathrm{are}\:\mathrm{in}\:\mathrm{use}...\:\mathrm{confusion}... \\ $$$$\mathrm{old}\:\mathrm{definition}\:\mathbb{N}=\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:...\right\};\:\mathbb{N}\cup\left\{\mathrm{0}\right\}=\mathbb{N}_{\mathrm{0}} \\ $$$$\mathrm{new}\:\mathrm{definition}\:\mathbb{N}=\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:...\right\};\:\mathbb{N}\backslash\left\{\mathrm{0}\right\}=\mathbb{N}^{\bigstar} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{depends}\:\mathrm{on}\:\mathrm{in}\:\mathrm{which}\:\mathrm{country} \\ $$$$\mathrm{and}\:\mathrm{on}\:\mathrm{which}\:\mathrm{school}\:\mathrm{you}\:\mathrm{are} \\ $$$$ \\ $$$$\mathrm{when}\:\mathrm{I}\:\mathrm{was}\:\mathrm{in}\:\mathrm{school}\:\left(\mathrm{a}\:\mathrm{zillion}\:\mathrm{years}\:\mathrm{ago}\right)\:\mathrm{we} \\ $$$$\mathrm{leaned}\:\mathrm{these}\:\mathrm{things}\:\mathrm{one}\:\mathrm{after}\:\mathrm{the}\:\mathrm{other}: \\ $$$$\left(\mathrm{1}\right)\:\mathbb{N}:\:{as}\:{you}\:{count}\:\left(\mathrm{nobody}\:\mathrm{would}\:\mathrm{start}\:\mathrm{to}\right. \\ $$$$\left.\:\:\:\:\:\mathrm{count}\:\mathrm{by}\:\mathrm{0}\right). \\ $$$$\left(\mathrm{1}.\mathrm{1}\right)\:\mathrm{addition}\:\mathrm{is}\:\mathrm{always}\:\mathrm{possible}\:\mathrm{in}\:\mathbb{N} \\ $$$$\left(\mathrm{1}.\mathrm{2}\right)\:\mathrm{multiplication}\:\mathrm{is}\:\mathrm{always}\:\mathrm{possible}\:\mathrm{in}\:\mathbb{N} \\ $$$$\:\:\:\:\:\mathrm{but}\:{n}×\mathrm{1}={n} \\ $$$$\left(\mathrm{1}.\mathrm{3}\right)\:\mathrm{substraction}\:\mathrm{only}\:\mathrm{as}\:\mathrm{a}\:\mathrm{test}\:\mathrm{of}\:\mathrm{addition} \\ $$$$\:\:\:\:\:{a}+{b}={c}\:\Rightarrow\:{c}−{b}={a}\wedge{c}−{a}={b} \\ $$$$\left(\mathrm{1}.\mathrm{4}\right)\:\mathrm{substraction}\:{a}−{b}\:\mathrm{possible}\:\mathrm{only}\:\mathrm{if}\:{a}>{b}? \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{2}\right)\:\mathbb{Z}=\mathbb{N}\cup\left\{...−\mathrm{2},\:−\mathrm{1},\:\mathrm{0}\right\}\:\mathrm{these}\:\mathrm{are}\:\mathrm{magical} \\ $$$$\:\:\:\:\:\mathrm{numbers}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{substract}\:\mathrm{without}\:\mathrm{limits} \\ $$$$\:\:\:\:\:{a}−{b}={x}\:\mathrm{always}\:\mathrm{solveable}\:\mathrm{in}\:\mathbb{Z} \\ $$$$\left(\mathrm{2}.\mathrm{1}\right)\:\mathrm{0}\:{neutral}\:{element}\:{of}\:{addition} \\ $$$$\left(\mathrm{2}.\mathrm{2}\right)\:\mathrm{1}\:{neutral}\:{element}\:{of}\:{multiplication} \\ $$$$ \\ $$$$\mathrm{then}\:\mathbb{Q}\:\left({a}\boldsymbol{\div}{b}={x}\:\mathrm{solveable}\right),\:\mathrm{then}\:\mathbb{R}\:\left(\mathrm{all}\:\mathrm{non}−\right. \\ $$$$\left.\mathrm{periodic}\:\mathrm{numbers}\:\mathrm{like}\:\sqrt{\mathrm{2}},\:\pi;\:\mathrm{later}\:\mathrm{e}...\right), \\ $$$$\mathrm{finally}\:\mathbb{C} \\ $$
Commented by Eric002 last updated on 21/Sep/20
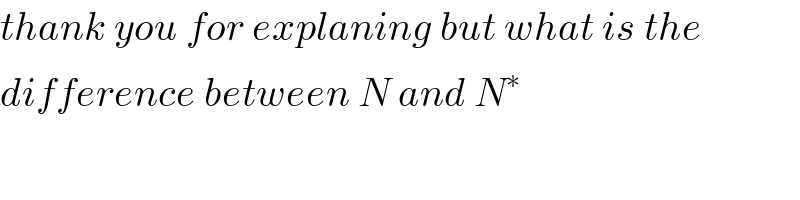
$${thank}\:{you}\:{for}\:{explaning}\:{but}\:{what}\:{is}\:{the} \\ $$$${difference}\:{between}\:{N}\:{and}\:{N}^{\ast} \\ $$
Commented by MJS_new last updated on 21/Sep/20

$$\mathrm{the}\:\mathrm{old}\:\mathbb{N}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{new}\:\mathbb{N}^{\bigstar} \\ $$$$=\left\{\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:...\right\} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{old}\:\mathbb{N}_{\mathrm{0}} \:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{new}\:\mathbb{N} \\ $$$$=\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:...\right\} \\ $$
Commented by Eric002 last updated on 21/Sep/20

$${thank}\:{you}\:{sir}\: \\ $$
Commented by Rasheed.Sindhi last updated on 21/Sep/20

$${Why}\:{isn}'{t}\:{there}\:{any}\:{international} \\ $$$${institute}\:{which}\:{play}\:{roll}\:{in}\:{this} \\ $$$${connection}?\:{Which}\:{make} \\ $$$${standards}\:{so}\:{that}\:\:{such} \\ $$$${confusions}\:{be}\:{killed}? \\ $$
Commented by MJS_new last updated on 21/Sep/20

$$\mathrm{standards}\:\mathrm{are}\:\mathrm{no}\:\mathrm{longer}\:\mathrm{accepted}\:\mathrm{in}\:\mathrm{the}\:\mathrm{age} \\ $$$$\mathrm{of}\:\mathrm{internet};\:\mathrm{everybody}'\mathrm{s}\:\mathrm{own}\:\mathrm{opinion}\:\mathrm{counts} \\ $$$$\mathrm{more}\:\mathrm{than}\:\mathrm{any}\:\mathrm{standard} \\ $$
Commented by Rasheed.Sindhi last updated on 21/Sep/20

$$\mathcal{T}{hank}\mathcal{S}{s}\:\mathcal{S}{ir}! \\ $$
