
Question Number 114753 by bemath last updated on 21/Sep/20
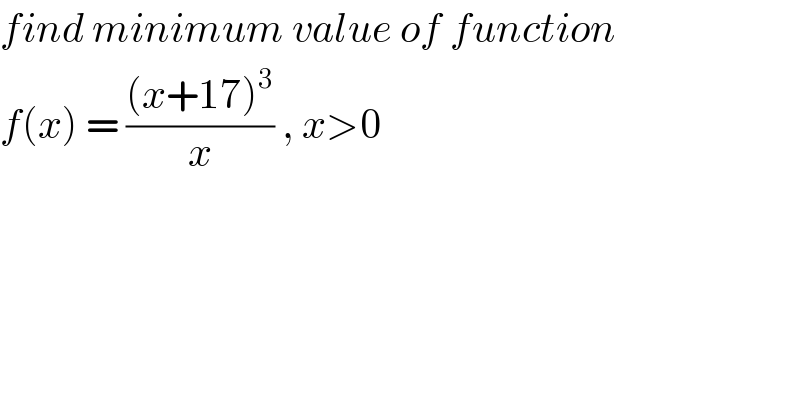
$${find}\:{minimum}\:{value}\:{of}\:{function} \\ $$ $${f}\left({x}\right)\:=\:\frac{\left({x}+\mathrm{17}\right)^{\mathrm{3}} }{{x}}\:,\:{x}>\mathrm{0} \\ $$
Answered by Olaf last updated on 21/Sep/20
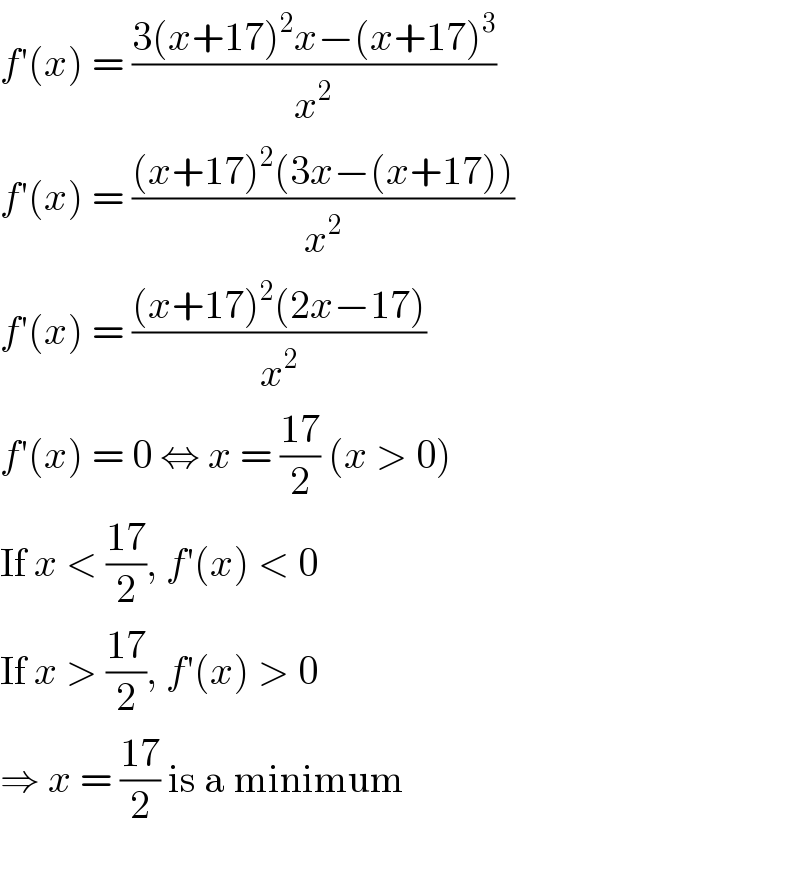
$${f}'\left({x}\right)\:=\:\frac{\mathrm{3}\left({x}+\mathrm{17}\right)^{\mathrm{2}} {x}−\left({x}+\mathrm{17}\right)^{\mathrm{3}} }{{x}^{\mathrm{2}} } \\ $$ $${f}'\left({x}\right)\:=\:\frac{\left({x}+\mathrm{17}\right)^{\mathrm{2}} \left(\mathrm{3}{x}−\left({x}+\mathrm{17}\right)\right)}{{x}^{\mathrm{2}} } \\ $$ $${f}'\left({x}\right)\:=\:\frac{\left({x}+\mathrm{17}\right)^{\mathrm{2}} \left(\mathrm{2}{x}−\mathrm{17}\right)}{{x}^{\mathrm{2}} } \\ $$ $${f}'\left({x}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:{x}\:=\:\frac{\mathrm{17}}{\mathrm{2}}\:\left({x}\:>\:\mathrm{0}\right) \\ $$ $$\mathrm{If}\:{x}\:<\:\frac{\mathrm{17}}{\mathrm{2}},\:{f}'\left({x}\right)\:<\:\mathrm{0} \\ $$ $$\mathrm{If}\:{x}\:>\:\frac{\mathrm{17}}{\mathrm{2}},\:{f}'\left({x}\right)\:>\:\mathrm{0} \\ $$ $$\Rightarrow\:{x}\:=\:\frac{\mathrm{17}}{\mathrm{2}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{minimum} \\ $$ $$ \\ $$
Commented bybemath last updated on 21/Sep/20

$${give}\:{thanks}\: \\ $$
