
Question Number 114637 by bobhans last updated on 20/Sep/20
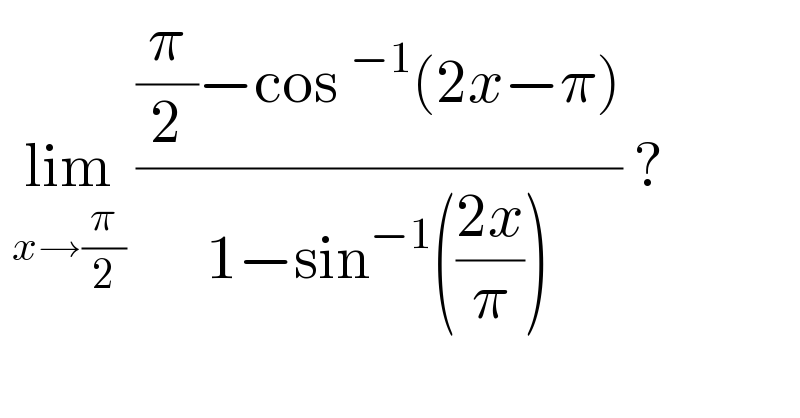
$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\frac{\pi}{\mathrm{2}}−\mathrm{cos}\:^{−\mathrm{1}} \left(\mathrm{2}{x}−\pi\right)}{\mathrm{1}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}}{\pi}\right)}\:? \\ $$
Answered by bemath last updated on 20/Sep/20
![setting x=(π/2)+p→2x=π+2p lim_(p→0) (((π/2)−cos^(−1) (2p))/(1−sin^(−1) (((π+2p)/π))))= lim_(p→0) (([(2/( (√(1−4p^2 ))))])/(−[((2/π)/( (√(1−(((π+2p)/π))^2 ))))])) = lim_(p→0) (2/( (√(1−4p^2 )))) × (−(2/(π(√(1−(((π+2p)/π))^2 ))))) = ∞](Q114640.png)
$${setting}\:{x}=\frac{\pi}{\mathrm{2}}+{p}\rightarrow\mathrm{2}{x}=\pi+\mathrm{2}{p} \\ $$$$\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\pi}{\mathrm{2}}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{2}{p}\right)}{\mathrm{1}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{\pi+\mathrm{2}{p}}{\pi}\right)}= \\ $$$$\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} }}\right]}{−\left[\frac{\frac{\mathrm{2}}{\pi}}{\:\sqrt{\mathrm{1}−\left(\frac{\pi+\mathrm{2}{p}}{\pi}\right)^{\mathrm{2}} }}\right]}\:= \\ $$$$\underset{{p}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{4}{p}^{\mathrm{2}} }}\:×\:\left(−\frac{\mathrm{2}}{\pi\sqrt{\mathrm{1}−\left(\frac{\pi+\mathrm{2}{p}}{\pi}\right)^{\mathrm{2}} }}\right)\:=\:\infty \\ $$$$ \\ $$
Commented by bobhans last updated on 20/Sep/20

$${gave}\:{kudos} \\ $$
