
Question Number 114593 by abdullahquwatan last updated on 19/Sep/20

$$\frac{\mid{x}−\mathrm{1}\mid}{\mid{x}\mid−\mathrm{1}}\:\leqslant\:\mathrm{1} \\ $$
Answered by MJS_new last updated on 19/Sep/20
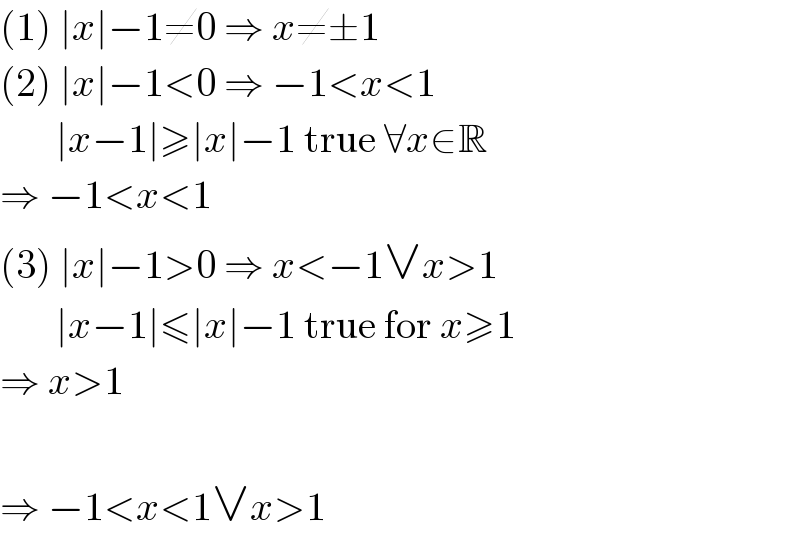
$$\left(\mathrm{1}\right)\:\mid{x}\mid−\mathrm{1}\neq\mathrm{0}\:\Rightarrow\:{x}\neq\pm\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\mid{x}\mid−\mathrm{1}<\mathrm{0}\:\Rightarrow\:−\mathrm{1}<{x}<\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\mid{x}−\mathrm{1}\mid\geqslant\mid{x}\mid−\mathrm{1}\:\mathrm{true}\:\forall{x}\in\mathbb{R} \\ $$$$\Rightarrow\:−\mathrm{1}<{x}<\mathrm{1} \\ $$$$\left(\mathrm{3}\right)\:\mid{x}\mid−\mathrm{1}>\mathrm{0}\:\Rightarrow\:{x}<−\mathrm{1}\vee{x}>\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\mid{x}−\mathrm{1}\mid\leqslant\mid{x}\mid−\mathrm{1}\:\mathrm{true}\:\mathrm{for}\:{x}\geqslant\mathrm{1} \\ $$$$\Rightarrow\:{x}>\mathrm{1} \\ $$$$ \\ $$$$\Rightarrow\:−\mathrm{1}<{x}<\mathrm{1}\vee{x}>\mathrm{1} \\ $$
Commented by abdullahquwatan last updated on 20/Sep/20

$${thanks}\:{sir} \\ $$
