
Question Number 114586 by Khalmohmmad last updated on 19/Sep/20
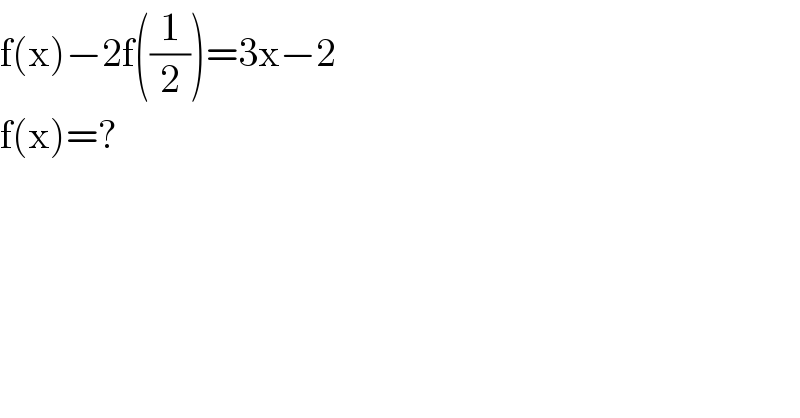
$$\mathrm{f}\left(\mathrm{x}\right)−\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{3x}−\mathrm{2} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=? \\ $$
Commented by Dwaipayan Shikari last updated on 19/Sep/20
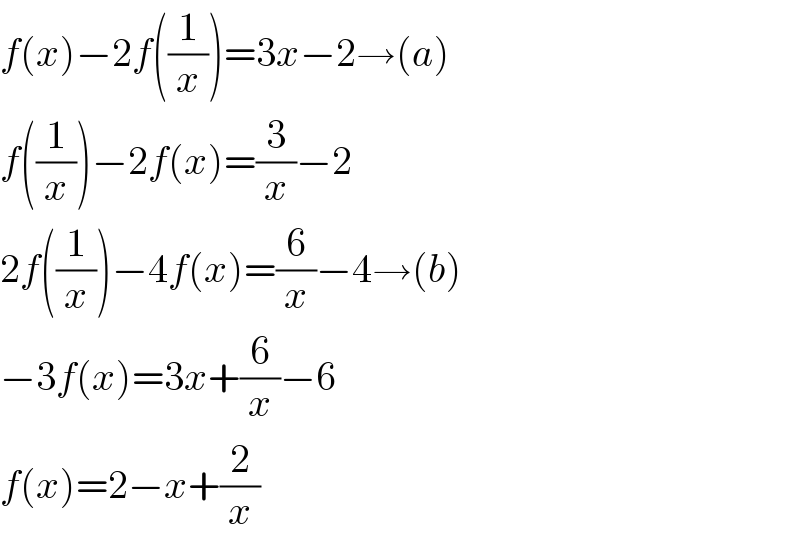
$${f}\left({x}\right)−\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)=\mathrm{3}{x}−\mathrm{2}\rightarrow\left({a}\right) \\ $$$${f}\left(\frac{\mathrm{1}}{{x}}\right)−\mathrm{2}{f}\left({x}\right)=\frac{\mathrm{3}}{{x}}−\mathrm{2} \\ $$$$\mathrm{2}{f}\left(\frac{\mathrm{1}}{{x}}\right)−\mathrm{4}{f}\left({x}\right)=\frac{\mathrm{6}}{{x}}−\mathrm{4}\rightarrow\left({b}\right) \\ $$$$−\mathrm{3}{f}\left({x}\right)=\mathrm{3}{x}+\frac{\mathrm{6}}{{x}}−\mathrm{6} \\ $$$${f}\left({x}\right)=\mathrm{2}−{x}+\frac{\mathrm{2}}{{x}} \\ $$
Commented by Aziztisffola last updated on 19/Sep/20

$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{or}\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)? \\ $$
Answered by Olaf last updated on 19/Sep/20
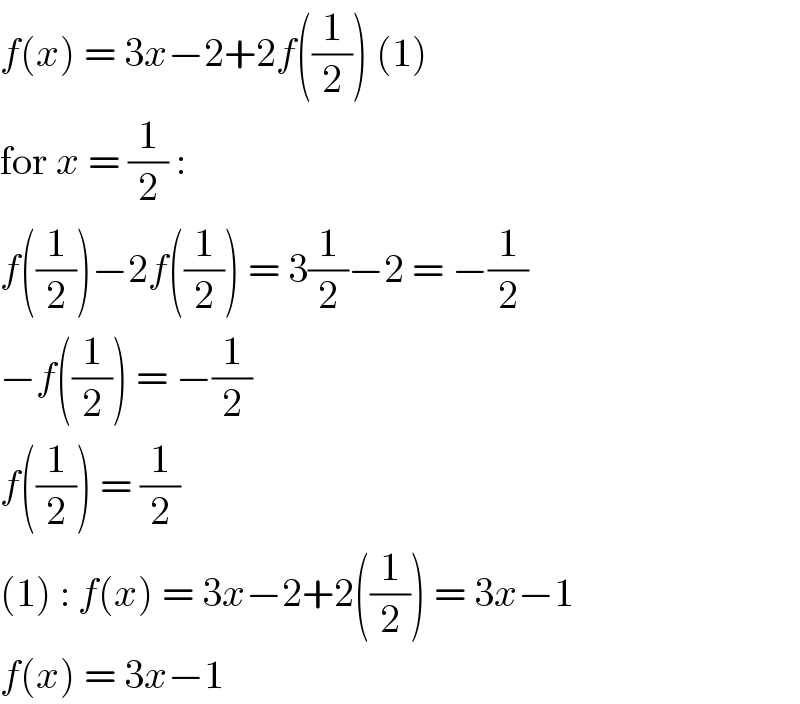
$${f}\left({x}\right)\:=\:\mathrm{3}{x}−\mathrm{2}+\mathrm{2}{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\left(\mathrm{1}\right) \\ $$$$\mathrm{for}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:: \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{3}\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$−{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\::\:{f}\left({x}\right)\:=\:\mathrm{3}{x}−\mathrm{2}+\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{3}{x}−\mathrm{1} \\ $$$${f}\left({x}\right)\:=\:\mathrm{3}{x}−\mathrm{1} \\ $$
