
Question Number 114551 by bemath last updated on 19/Sep/20
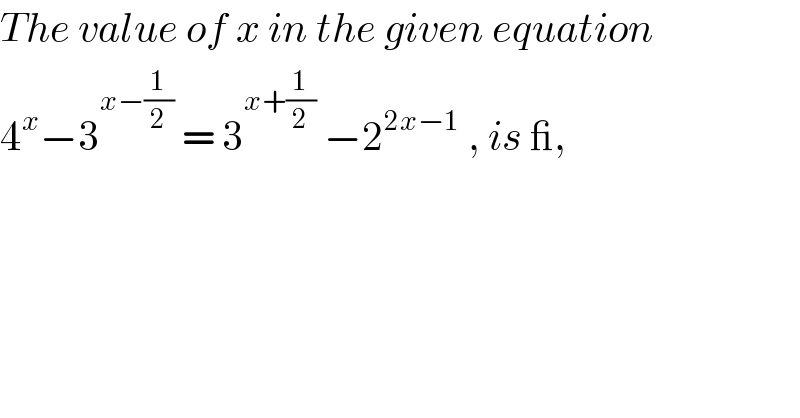
$${The}\:{value}\:{of}\:{x}\:{in}\:{the}\:{given}\:{equation} \\ $$$$\mathrm{4}^{{x}} −\mathrm{3}^{{x}−\frac{\mathrm{1}}{\mathrm{2}}} \:=\:\mathrm{3}^{{x}+\frac{\mathrm{1}}{\mathrm{2}}} \:−\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} \:,\:{is}\:\_, \\ $$
Commented by Dwaipayan Shikari last updated on 19/Sep/20
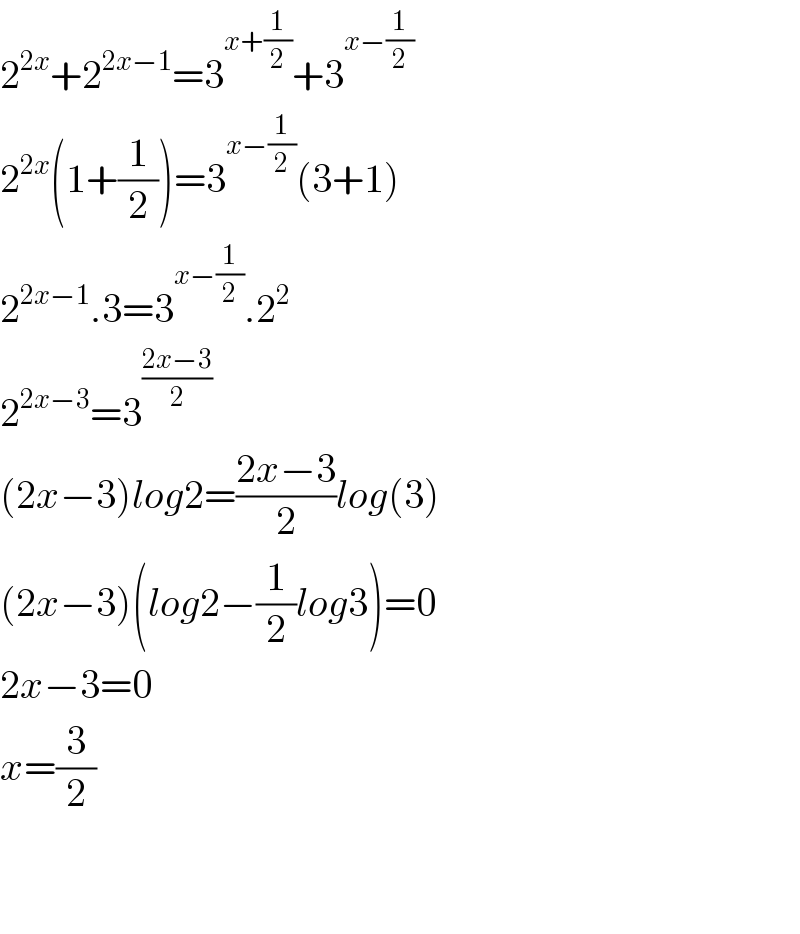
$$\mathrm{2}^{\mathrm{2}{x}} +\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} =\mathrm{3}^{{x}+\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{3}^{{x}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{3}^{{x}−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{3}+\mathrm{1}\right) \\ $$$$\mathrm{2}^{\mathrm{2}{x}−\mathrm{1}} .\mathrm{3}=\mathrm{3}^{{x}−\frac{\mathrm{1}}{\mathrm{2}}} .\mathrm{2}^{\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{2}{x}−\mathrm{3}} =\mathrm{3}^{\frac{\mathrm{2}{x}−\mathrm{3}}{\mathrm{2}}} \\ $$$$\left(\mathrm{2}{x}−\mathrm{3}\right){log}\mathrm{2}=\frac{\mathrm{2}{x}−\mathrm{3}}{\mathrm{2}}{log}\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}{x}−\mathrm{3}\right)\left({log}\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}{log}\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 19/Sep/20
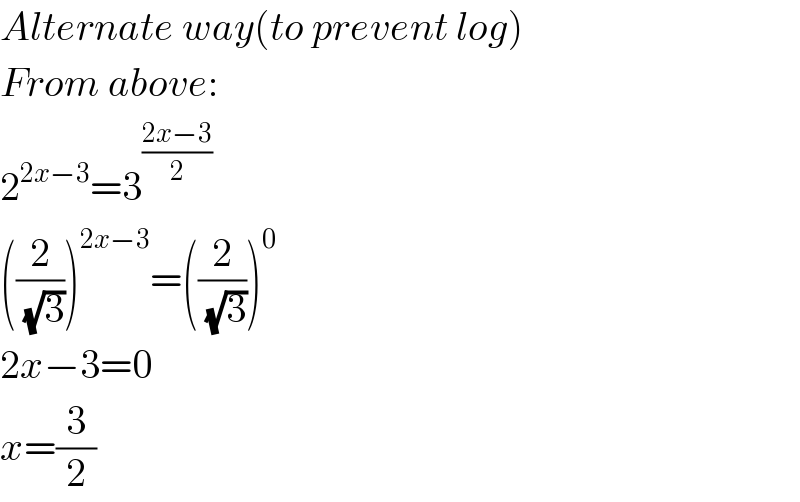
$${Alternate}\:{way}\left({to}\:{prevent}\:{log}\right)\: \\ $$$${From}\:{above}: \\ $$$$\mathrm{2}^{\mathrm{2}{x}−\mathrm{3}} =\mathrm{3}^{\frac{\mathrm{2}{x}−\mathrm{3}}{\mathrm{2}}} \\ $$$$\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}{x}−\mathrm{3}} =\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{0}} \\ $$$$\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 19/Sep/20

$${Yes}\:{sir}! \\ $$
Answered by bobhans last updated on 19/Sep/20
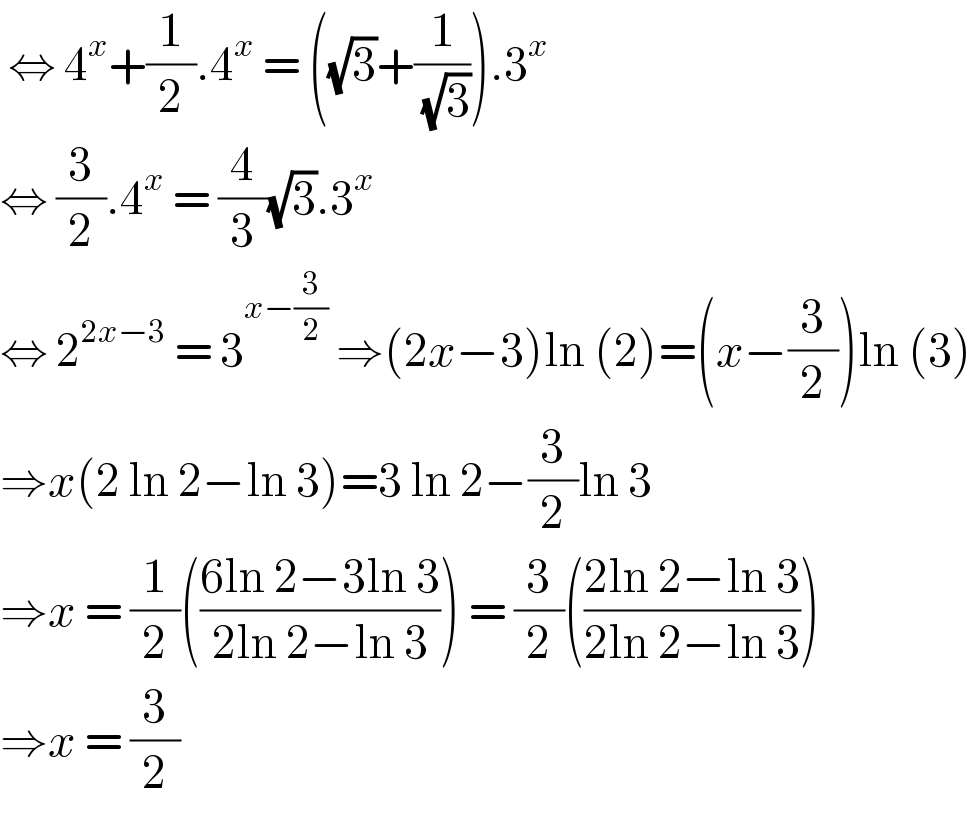
$$\:\Leftrightarrow\:\mathrm{4}^{{x}} +\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{4}^{{x}} \:=\:\left(\sqrt{\mathrm{3}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right).\mathrm{3}^{{x}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{3}}{\mathrm{2}}.\mathrm{4}^{{x}} \:=\:\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{3}}.\mathrm{3}^{{x}} \\ $$$$\Leftrightarrow\:\mathrm{2}^{\mathrm{2}{x}−\mathrm{3}} \:=\:\mathrm{3}^{{x}−\frac{\mathrm{3}}{\mathrm{2}}} \:\Rightarrow\left(\mathrm{2}{x}−\mathrm{3}\right)\mathrm{ln}\:\left(\mathrm{2}\right)=\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)\mathrm{ln}\:\left(\mathrm{3}\right) \\ $$$$\Rightarrow{x}\left(\mathrm{2}\:\mathrm{ln}\:\mathrm{2}−\mathrm{ln}\:\mathrm{3}\right)=\mathrm{3}\:\mathrm{ln}\:\mathrm{2}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\mathrm{3} \\ $$$$\Rightarrow{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{6ln}\:\mathrm{2}−\mathrm{3ln}\:\mathrm{3}}{\mathrm{2ln}\:\mathrm{2}−\mathrm{ln}\:\mathrm{3}}\right)\:=\:\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{2ln}\:\mathrm{2}−\mathrm{ln}\:\mathrm{3}}{\mathrm{2ln}\:\mathrm{2}−\mathrm{ln}\:\mathrm{3}}\right) \\ $$$$\Rightarrow{x}\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by bemath last updated on 19/Sep/20

$${gave}\:{kudos}\: \\ $$
