
Question Number 114526 by bobhans last updated on 19/Sep/20
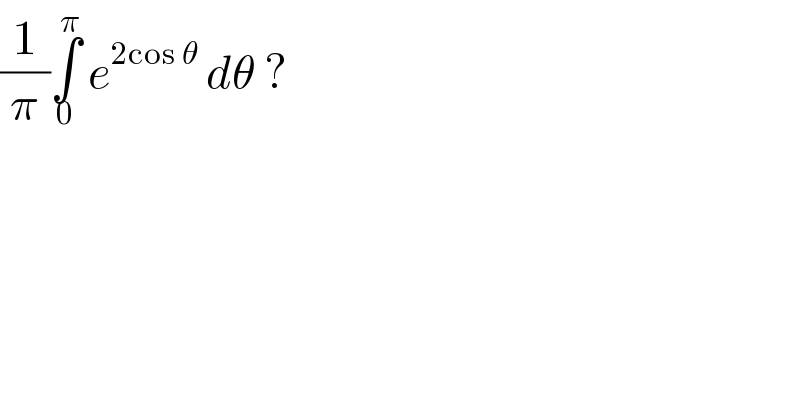
$$\frac{\mathrm{1}}{\pi}\underset{\mathrm{0}} {\overset{\pi} {\int}}\:{e}^{\mathrm{2cos}\:\theta} \:{d}\theta\:? \\ $$
Commented by JDamian last updated on 19/Sep/20
https://youtu.be/-UhFu0g9740
Commented by mathmax by abdo last updated on 19/Sep/20
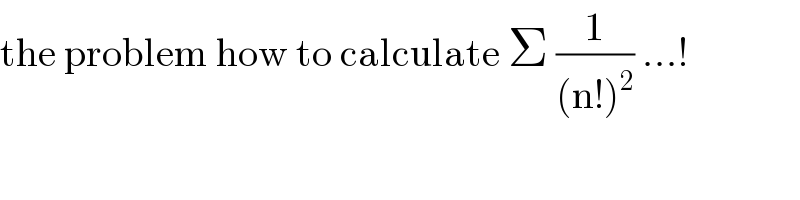
$$\mathrm{the}\:\mathrm{problem}\:\mathrm{how}\:\mathrm{to}\:\mathrm{calculate}\:\Sigma\:\frac{\mathrm{1}}{\left(\mathrm{n}!\right)^{\mathrm{2}} }\:...! \\ $$
Answered by mathmax by abdo last updated on 19/Sep/20

$$\mathrm{I}\:=\frac{\mathrm{1}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{\mathrm{2cos}\theta} \:\mathrm{d}\theta\:\Rightarrow\pi\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{e}^{\mathrm{2cos}\theta} \:\mathrm{d}\theta\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \:\mathrm{e}^{\mathrm{2cos}\theta} \:\mathrm{d}\theta\left(\rightarrow\theta=\frac{\pi}{\mathrm{2}}+\mathrm{u}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{e}^{\mathrm{2cos}\theta} \:\mathrm{d}\theta\:\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{2sinu}} \:\mathrm{du}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{2cos}\theta\right)^{\mathrm{n}} }{\mathrm{n}!}\:\mathrm{d}\theta \\ $$$$+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{2sin}\theta\right)^{\mathrm{n}} }{\mathrm{n}!}\:\mathrm{d}\theta\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{n}!}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{n}} \theta\:\mathrm{d}\theta \\ $$$$+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{2}\right)^{\mathrm{n}} }{\mathrm{n}!}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{n}} \theta\:\mathrm{d}\theta\:\:\mathrm{changement}\:\:\theta\:=\frac{\pi}{\mathrm{2}}−\mathrm{t}\:\mathrm{give} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{n}} \theta\:\mathrm{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{n}} \mathrm{t}\:\mathrm{dt}\:\Rightarrow \\ $$$$\pi\:\mathrm{I}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left\{\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{n}!}\:+\frac{\left(−\mathrm{2}\right)^{\mathrm{n}} }{\mathrm{n}!}\right\}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{n}} \theta\:\mathrm{d}\theta\:\:\mathrm{let}\:\mathrm{w}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{n}} \theta\:\mathrm{d}\theta\:\left(\mathrm{wallis}\:\mathrm{integral}\right) \\ $$$$\pi\mathrm{I}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{\mathrm{n}} }{\mathrm{n}!}\left(\mathrm{1}+\left(−\mathrm{1}\right)^{\mathrm{n}} \right)\mathrm{W}_{\mathrm{n}} \:\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{\mathrm{2n}} }{\left(\mathrm{2n}\right)!}\left(\mathrm{2}\right)\mathrm{W}_{\mathrm{2n}} \:\Rightarrow \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\pi}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }{\left(\mathrm{2n}\right)!}\:\mathrm{W}_{\mathrm{2n}} \:\:\:\:\:\left(\mathrm{w}_{\mathrm{2n}} \mathrm{is}\:\mathrm{known}\:\mathrm{by}\:\mathrm{recurrence}\right) \\ $$$$ \\ $$
