
Question Number 114512 by Rio Michael last updated on 19/Sep/20

Commented by Rio Michael last updated on 19/Sep/20
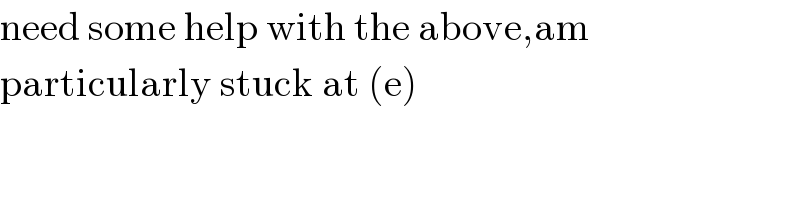
$$\mathrm{need}\:\mathrm{some}\:\mathrm{help}\:\mathrm{with}\:\mathrm{the}\:\mathrm{above},\mathrm{am} \\ $$$$\mathrm{particularly}\:\mathrm{stuck}\:\mathrm{at}\:\left(\mathrm{e}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 19/Sep/20
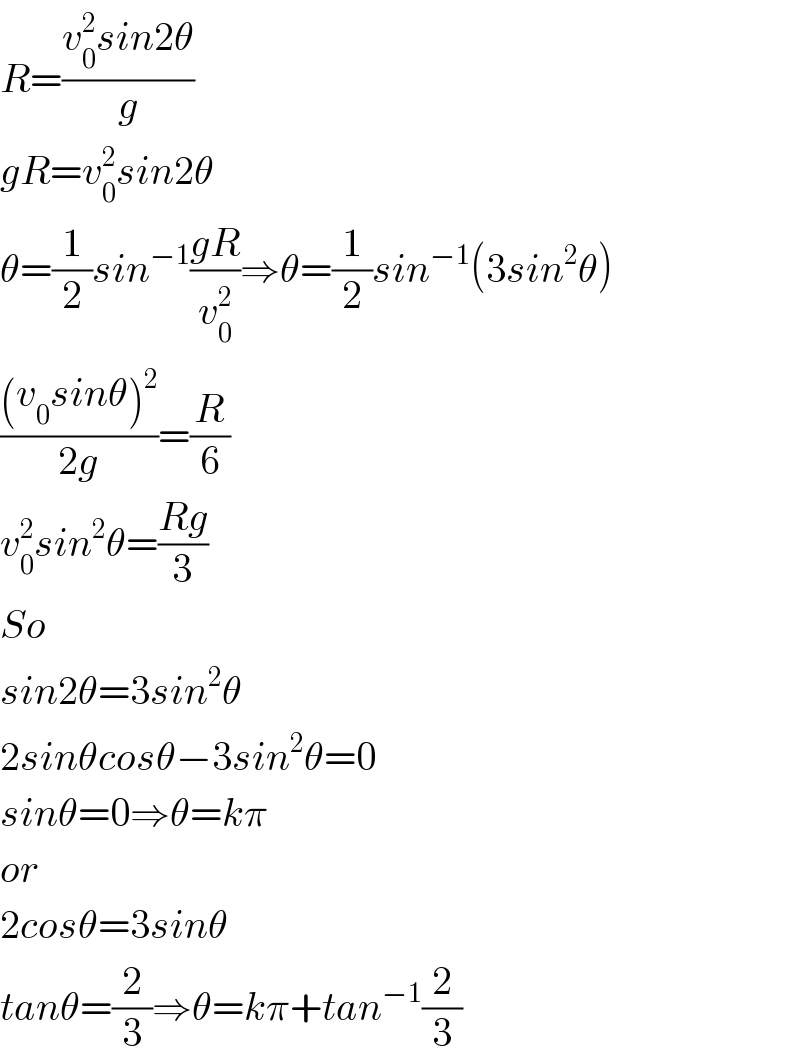
$${R}=\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} {sin}\mathrm{2}\theta}{{g}} \\ $$$${gR}={v}_{\mathrm{0}} ^{\mathrm{2}} {sin}\mathrm{2}\theta \\ $$$$\theta=\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{{gR}}{{v}_{\mathrm{0}} ^{\mathrm{2}} }\Rightarrow\theta=\frac{\mathrm{1}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\mathrm{3}{sin}^{\mathrm{2}} \theta\right) \\ $$$$\frac{\left({v}_{\mathrm{0}} {sin}\theta\right)^{\mathrm{2}} }{\mathrm{2}{g}}=\frac{{R}}{\mathrm{6}} \\ $$$${v}_{\mathrm{0}} ^{\mathrm{2}} {sin}^{\mathrm{2}} \theta=\frac{{Rg}}{\mathrm{3}} \\ $$$${So} \\ $$$${sin}\mathrm{2}\theta=\mathrm{3}{sin}^{\mathrm{2}} \theta \\ $$$$\mathrm{2}{sin}\theta{cos}\theta−\mathrm{3}{sin}^{\mathrm{2}} \theta=\mathrm{0} \\ $$$${sin}\theta=\mathrm{0}\Rightarrow\theta={k}\pi \\ $$$${or} \\ $$$$\mathrm{2}{cos}\theta=\mathrm{3}{sin}\theta \\ $$$${tan}\theta=\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow\theta={k}\pi+{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by Rio Michael last updated on 19/Sep/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\: \\ $$
Commented by Rio Michael last updated on 19/Sep/20

$$\mathrm{but}\:\mathrm{sir}\:\mathrm{what}\:\mathrm{if}\:{v}_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{is}\:\mathrm{also}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\theta_{\mathrm{0}} \\ $$
Answered by mr W last updated on 19/Sep/20
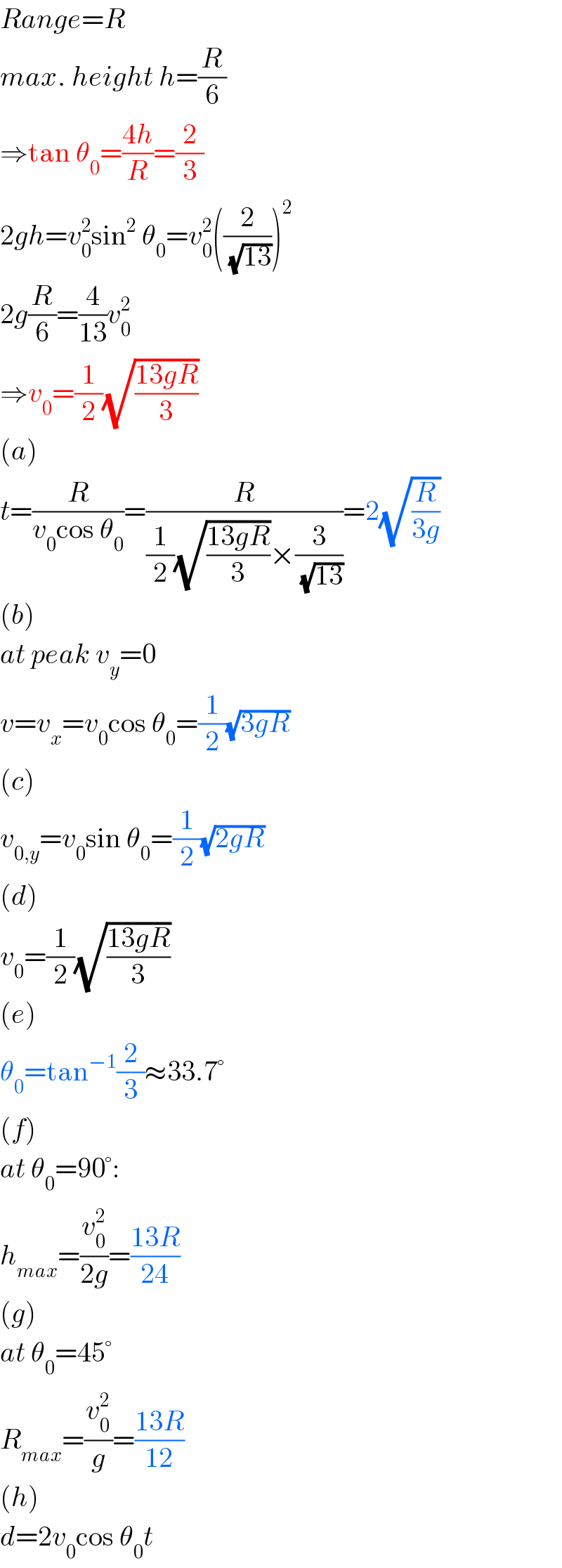
$${Range}={R} \\ $$$${max}.\:{height}\:{h}=\frac{{R}}{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{tan}\:\theta_{\mathrm{0}} =\frac{\mathrm{4}{h}}{{R}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{2}{gh}={v}_{\mathrm{0}} ^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{0}} ={v}_{\mathrm{0}} ^{\mathrm{2}} \left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{g}\frac{{R}}{\mathrm{6}}=\frac{\mathrm{4}}{\mathrm{13}}{v}_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\Rightarrow{v}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{13}{gR}}{\mathrm{3}}} \\ $$$$\left({a}\right) \\ $$$${t}=\frac{{R}}{{v}_{\mathrm{0}} \mathrm{cos}\:\theta_{\mathrm{0}} }=\frac{{R}}{\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{13}{gR}}{\mathrm{3}}}×\frac{\mathrm{3}}{\:\sqrt{\mathrm{13}}}}=\mathrm{2}\sqrt{\frac{{R}}{\mathrm{3}{g}}} \\ $$$$\left({b}\right) \\ $$$${at}\:{peak}\:{v}_{{y}} =\mathrm{0} \\ $$$${v}={v}_{{x}} ={v}_{\mathrm{0}} \mathrm{cos}\:\theta_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}{gR}} \\ $$$$\left({c}\right) \\ $$$${v}_{\mathrm{0},{y}} ={v}_{\mathrm{0}} \mathrm{sin}\:\theta_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}{gR}} \\ $$$$\left({d}\right) \\ $$$${v}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\mathrm{13}{gR}}{\mathrm{3}}} \\ $$$$\left({e}\right) \\ $$$$\theta_{\mathrm{0}} =\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\approx\mathrm{33}.\mathrm{7}° \\ $$$$\left({f}\right) \\ $$$${at}\:\theta_{\mathrm{0}} =\mathrm{90}°: \\ $$$${h}_{{max}} =\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{\mathrm{2}{g}}=\frac{\mathrm{13}{R}}{\mathrm{24}} \\ $$$$\left({g}\right) \\ $$$${at}\:\theta_{\mathrm{0}} =\mathrm{45}° \\ $$$${R}_{{max}} =\frac{{v}_{\mathrm{0}} ^{\mathrm{2}} }{{g}}=\frac{\mathrm{13}{R}}{\mathrm{12}} \\ $$$$\left({h}\right) \\ $$$${d}=\mathrm{2}{v}_{\mathrm{0}} \mathrm{cos}\:\theta_{\mathrm{0}} {t} \\ $$
Commented by Rio Michael last updated on 20/Sep/20
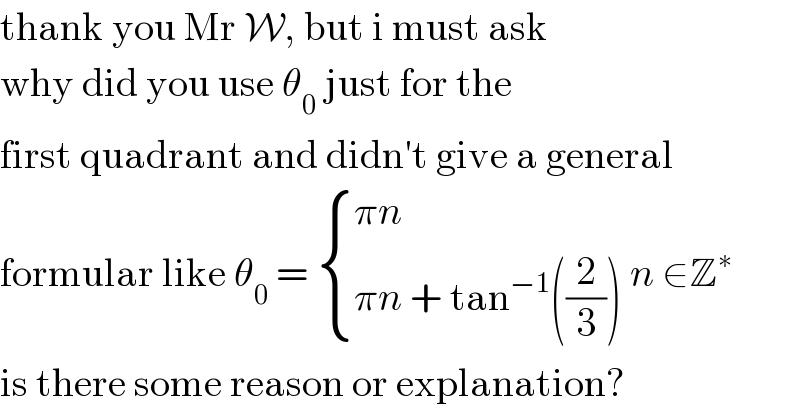
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Mr}\:\mathcal{W},\:\mathrm{but}\:\mathrm{i}\:\mathrm{must}\:\mathrm{ask} \\ $$$$\mathrm{why}\:\mathrm{did}\:\mathrm{you}\:\mathrm{use}\:\theta_{\mathrm{0}} \:\mathrm{just}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{first}\:\mathrm{quadrant}\:\mathrm{and}\:\mathrm{didn}'\mathrm{t}\:\mathrm{give}\:\mathrm{a}\:\mathrm{general} \\ $$$$\mathrm{formular}\:\mathrm{like}\:\theta_{\mathrm{0}} \:=\:\begin{cases}{\pi{n}}\\{\pi{n}\:+\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)}\end{cases}\:{n}\:\in\mathbb{Z}^{\ast} \\ $$$$\mathrm{is}\:\mathrm{there}\:\mathrm{some}\:\mathrm{reason}\:\mathrm{or}\:\mathrm{explanation}? \\ $$
Commented by mr W last updated on 21/Sep/20
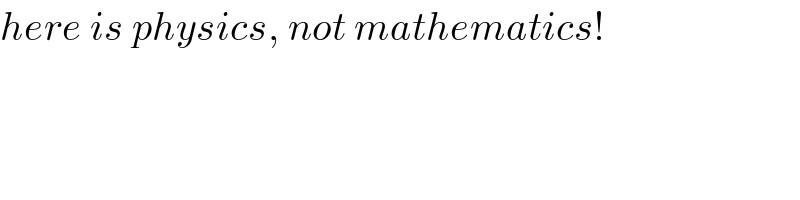
$${here}\:{is}\:{physics},\:{not}\:{mathematics}! \\ $$
Commented by mr W last updated on 21/Sep/20
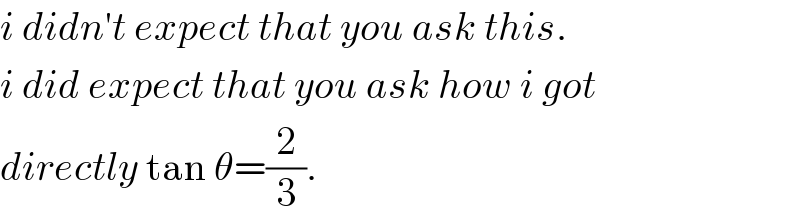
$${i}\:{didn}'{t}\:{expect}\:{that}\:{you}\:{ask}\:{this}. \\ $$$${i}\:{did}\:{expect}\:{that}\:{you}\:{ask}\:{how}\:{i}\:{got} \\ $$$${directly}\:\mathrm{tan}\:\theta=\frac{\mathrm{2}}{\mathrm{3}}. \\ $$
