
Question Number 114467 by Eric002 last updated on 19/Sep/20
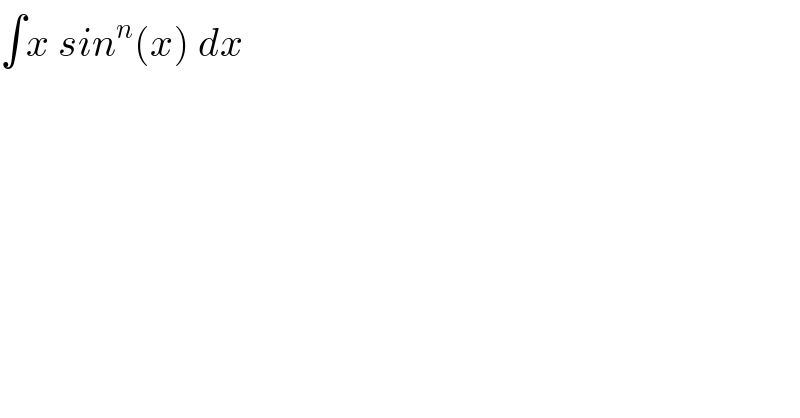
$$\int{x}\:{sin}^{{n}} \left({x}\right)\:{dx} \\ $$
Answered by Olaf last updated on 19/Sep/20

$$\mathrm{I}_{{n}} \left({x}\right)\:=\:\int{x}\mathrm{sin}^{{n}} {xdx} \\ $$$$\mathrm{I}_{{n}} \left({x}\right)−\mathrm{I}_{{n}+\mathrm{2}} \left({x}\right)\:=\:\int{x}\mathrm{sin}^{{n}} {x}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}\right){dx} \\ $$$$\mathrm{I}_{{n}} \left({x}\right)−\mathrm{I}_{{n}+\mathrm{2}} \left({x}\right)\:=\:\int\left({x}\mathrm{cos}{x}\right)\left(\mathrm{cos}{x}\mathrm{sin}^{{n}} {x}\right){dx} \\ $$$${u}\:=\:{x}\mathrm{cos}{x},\:{u}'\:=\:\mathrm{cos}{x}−{x}\mathrm{sin}{x} \\ $$$${v}'\:=\:\mathrm{cos}{x}\mathrm{sin}^{{n}} {x},\:{v}\:=\:\frac{\mathrm{sin}^{{n}+\mathrm{1}} {x}}{{n}+\mathrm{1}} \\ $$$$\mathrm{I}_{{n}} \left({x}\right)−\mathrm{I}_{{n}+\mathrm{2}} \left({x}\right)\:=\:\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}\mathrm{cos}{x}\mathrm{sin}^{{n}+\mathrm{1}} {x} \\ $$$$−\int\left(\mathrm{cos}{x}−{x}\mathrm{sin}{x}\right)\frac{\mathrm{sin}^{{n}+\mathrm{1}} {x}}{{n}+\mathrm{1}}{dx} \\ $$$$\mathrm{I}_{{n}} \left({x}\right)−\mathrm{I}_{{n}+\mathrm{2}} \left({x}\right)\:=\:\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}\mathrm{cos}{x}\mathrm{sin}^{{n}+\mathrm{1}} {x} \\ $$$$−\frac{\mathrm{1}}{{n}+\mathrm{1}}\int\mathrm{cos}{x}\mathrm{sin}^{{n}+\mathrm{1}} {xdx}+\frac{\mathrm{1}}{{n}+\mathrm{1}}\int{x}\mathrm{sin}^{{n}+\mathrm{2}} {xdx} \\ $$$$\mathrm{I}_{{n}} \left({x}\right)−\mathrm{I}_{{n}+\mathrm{2}} \left({x}\right)\:=\:\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}\mathrm{cos}{x}\mathrm{sin}^{{n}+\mathrm{1}} {x} \\ $$$$−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\mathrm{sin}^{{n}+\mathrm{2}} {x}+\frac{\mathrm{1}}{{n}+\mathrm{1}}\mathrm{I}_{{n}+\mathrm{2}} \left({x}\right) \\ $$$$ \\ $$$$\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}\mathrm{I}_{{n}+\mathrm{2}} \left({x}\right)−\mathrm{I}_{{n}} \left({x}\right)\:=\:\frac{\mathrm{sin}^{{n}+\mathrm{1}} {x}}{{n}+\mathrm{1}}\left(\frac{\mathrm{sin}{x}}{{n}+\mathrm{2}}−{x}\mathrm{cos}{x}\right) \\ $$$$\mathrm{I}_{{n}+\mathrm{2}} \left({x}\right)\:=\:\frac{{n}+\mathrm{1}}{{n}+\mathrm{2}}\mathrm{I}_{{n}} \left({x}\right)+\:\frac{\mathrm{sin}^{{n}+\mathrm{1}} {x}}{{n}+\mathrm{2}}\left(\frac{\mathrm{sin}{x}}{{n}+\mathrm{2}}−{x}\mathrm{cos}{x}\right) \\ $$$$\mathrm{and}\:\mathrm{I}_{\mathrm{0}} \left({x}\right)\:=\:\int{xdx}\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{1}} \left({x}\right)\:=\:\int{x}\mathrm{sin}{xdx}\:=\:\mathrm{sin}{x}−{x}\mathrm{cos}{x} \\ $$$$\mathrm{work}\:\mathrm{in}\:\mathrm{progress}... \\ $$
Commented by Eric002 last updated on 19/Sep/20

$${well}\:{done} \\ $$
