
Question Number 114461 by Jamshidbek2311 last updated on 19/Sep/20
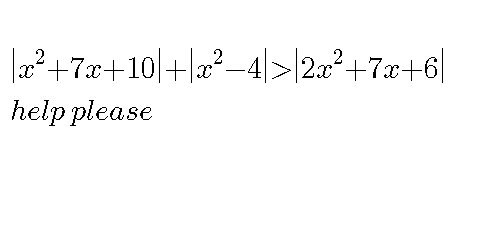
Commented by bemath last updated on 19/Sep/20
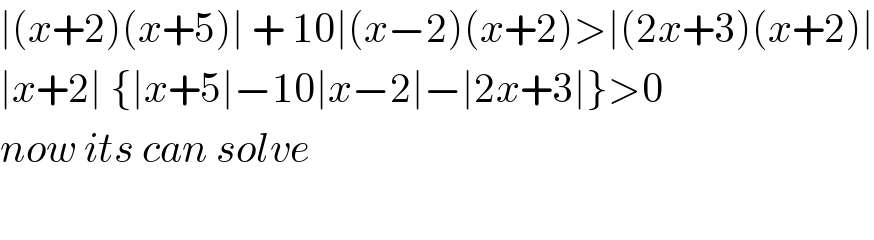
$$\mid\left({x}+\mathrm{2}\right)\left({x}+\mathrm{5}\right)\mid\:+\:\mathrm{10}\mid\left({x}−\mathrm{2}\right)\left({x}+\mathrm{2}\right)>\mid\left(\mathrm{2}{x}+\mathrm{3}\right)\left({x}+\mathrm{2}\right)\mid \\ $$$$\mid{x}+\mathrm{2}\mid\:\left\{\mid{x}+\mathrm{5}\mid−\mathrm{10}\mid{x}−\mathrm{2}\mid−\mid\mathrm{2}{x}+\mathrm{3}\mid\right\}>\mathrm{0} \\ $$$${now}\:{its}\:{can}\:{solve} \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 19/Sep/20
![Solve:∣x^2 +7x+10∣+∣x^2 −4∣>∣2x^2 +7x+6∣(1) x^2 +7x+10=(x+2)(x+5)≥0⇔x∈(−∞;−5)∪(−2;+∞) (x^2 −4)≥0⇔x∈(−∞;−2)∪(2;+∞) 2x^2 +7x+6≥0⇔(2x+3)(x+2)≥0⇔x∈(−∞;−2)∪(−(3/2);+∞) Hence we have followingtablet: determinant ((x,,(−5),,(−2),,(−(3/2)),,2,),(A,(x^2 +7x+10),0,(−x^2 −7x−10),0,(x^2 +7x+10),,(x^2 +7x+10),,(x^2 +7x+10)),(B,(x^2 −4),,(x^2 −4),,(4−x^2 ),,(4−x^2 ),0,(x^2 −4)),(C,(2x^2 +7x+6),,(2x^2 +7x+6),0,(−2x^2 −7x−6),0,(2x^2 +7x+6),,(2x^2 +7x+6))) From above we get i)For x∈(−∞;−5] (1)⇔2x^2 +7x+7>2x^2 +7x+6⇔has no roots ii)For x∈(−5;−2] (1)⇔−7x−14>2x^2 +7x+6 ⇔2x^2 +14x+20<0⇔x^2 +7x+10<0 ⇔(x+2)(x+5)<0⇔x∈ (−5;−2) we has the roots:x∈(−5;−2) iii)For x∈(−2;−(3/2)] (1)⇔7x+14>−2x^2 −7x−6 ⇔2x^2 +14x+20>0⇔x^2 +7x+10>0 ⇔(x+2)(x+5)>0⇔x∈(−∞;−5)∪(−2;+∞) we have the roots x∈(−2;−(3/2)) iv)For x∈(((−3)/2);2] (1)⇔7x+14>2x^2 +7x+6 ⇔2x^2 −8<0⇔x^2 −4<0⇔x∈(−2;2) we have the roots x∈(((−3)/2);2) v)For x∈(2;+∞) (1)⇔2x^2 +7x+6>2x^2 +7x+6 This inequality has no roots Combining five cases we get the roots of given inequality are: x∈(−5;−2)∪(−2;−(3/2))∪(−(3/2);2) or∈(−5;2)\{−2;−(3/2)}](Q114488.png)
$$\mathrm{Solve}:\mid\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{10}\mid+\mid\mathrm{x}^{\mathrm{2}} −\mathrm{4}\mid>\mid\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6}\mid\left(\mathrm{1}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{10}=\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{5}\right)\geqslant\mathrm{0}\Leftrightarrow\mathrm{x}\in\left(−\infty;−\mathrm{5}\right)\cup\left(−\mathrm{2};+\infty\right) \\ $$$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}\right)\geqslant\mathrm{0}\Leftrightarrow\mathrm{x}\in\left(−\infty;−\mathrm{2}\right)\cup\left(\mathrm{2};+\infty\right) \\ $$$$\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6}\geqslant\mathrm{0}\Leftrightarrow\left(\mathrm{2x}+\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2}\right)\geqslant\mathrm{0}\Leftrightarrow\mathrm{x}\in\left(−\infty;−\mathrm{2}\right)\cup\left(−\frac{\mathrm{3}}{\mathrm{2}};+\infty\right) \\ $$$$\mathrm{Hence}\:\mathrm{we}\:\mathrm{have}\:\mathrm{followingtablet}: \\ $$$$\begin{vmatrix}{\mathrm{x}}&{}&{−\mathrm{5}}&{}&{−\mathrm{2}}&{}&{−\frac{\mathrm{3}}{\mathrm{2}}}&{}&{\mathrm{2}}&{}\\{\mathrm{A}}&{\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{10}}&{\mathrm{0}}&{−\mathrm{x}^{\mathrm{2}} −\mathrm{7x}−\mathrm{10}}&{\mathrm{0}}&{\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{10}}&{}&{\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{10}}&{}&{\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{10}}\\{\mathrm{B}}&{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}&{}&{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}&{}&{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }&{}&{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }&{\mathrm{0}}&{\mathrm{x}^{\mathrm{2}} −\mathrm{4}}\\{\mathrm{C}}&{\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6}}&{}&{\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6}}&{\mathrm{0}}&{−\mathrm{2x}^{\mathrm{2}} −\mathrm{7x}−\mathrm{6}}&{\mathrm{0}}&{\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6}}&{}&{\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6}}\end{vmatrix} \\ $$$$\mathrm{From}\:\mathrm{above}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left.\mathrm{i}\right)\mathrm{For}\:\mathrm{x}\in\left(−\infty;−\mathrm{5}\right] \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{7}>\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6}\Leftrightarrow\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\left.\mathrm{ii}\right)\mathrm{For}\:\mathrm{x}\in\left(−\mathrm{5};−\mathrm{2}\right] \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow−\mathrm{7x}−\mathrm{14}>\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6} \\ $$$$\Leftrightarrow\mathrm{2x}^{\mathrm{2}} +\mathrm{14x}+\mathrm{20}<\mathrm{0}\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{10}<\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{5}\right)<\mathrm{0}\Leftrightarrow\mathrm{x}\in\:\left(−\mathrm{5};−\mathrm{2}\right) \\ $$$$\mathrm{we}\:\mathrm{has}\:\mathrm{the}\:\mathrm{roots}:\mathrm{x}\in\left(−\mathrm{5};−\mathrm{2}\right) \\ $$$$\left.\mathrm{iii}\right)\mathrm{For}\:\mathrm{x}\in\left(−\mathrm{2};−\frac{\mathrm{3}}{\mathrm{2}}\right] \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{7x}+\mathrm{14}>−\mathrm{2x}^{\mathrm{2}} −\mathrm{7x}−\mathrm{6} \\ $$$$\Leftrightarrow\mathrm{2x}^{\mathrm{2}} +\mathrm{14x}+\mathrm{20}>\mathrm{0}\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{10}>\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{5}\right)>\mathrm{0}\Leftrightarrow\mathrm{x}\in\left(−\infty;−\mathrm{5}\right)\cup\left(−\mathrm{2};+\infty\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{roots} \\ $$$$\mathrm{x}\in\left(−\mathrm{2};−\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$\left.\mathrm{iv}\right)\mathrm{For}\:\mathrm{x}\in\left(\frac{−\mathrm{3}}{\mathrm{2}};\mathrm{2}\right] \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{7x}+\mathrm{14}>\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6} \\ $$$$\Leftrightarrow\mathrm{2x}^{\mathrm{2}} −\mathrm{8}<\mathrm{0}\Leftrightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4}<\mathrm{0}\Leftrightarrow\mathrm{x}\in\left(−\mathrm{2};\mathrm{2}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{x}\in\left(\frac{−\mathrm{3}}{\mathrm{2}};\mathrm{2}\right) \\ $$$$\left.\mathrm{v}\right)\mathrm{For}\:\mathrm{x}\in\left(\mathrm{2};+\infty\right) \\ $$$$\left(\mathrm{1}\right)\Leftrightarrow\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6}>\mathrm{2x}^{\mathrm{2}} +\mathrm{7x}+\mathrm{6} \\ $$$$\mathrm{This}\:\mathrm{inequality}\:\mathrm{has}\:\mathrm{no}\:\mathrm{roots} \\ $$$$\mathrm{Combining}\:\mathrm{five}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{roots} \\ $$$$\mathrm{of}\:\mathrm{given}\:\mathrm{inequality}\:\mathrm{are}: \\ $$$$\mathrm{x}\in\left(−\mathrm{5};−\mathrm{2}\right)\cup\left(−\mathrm{2};−\frac{\mathrm{3}}{\mathrm{2}}\right)\cup\left(−\frac{\mathrm{3}}{\mathrm{2}};\mathrm{2}\right) \\ $$$$\mathrm{or}\in\left(−\mathrm{5};\mathrm{2}\right)\backslash\left\{−\mathrm{2};−\frac{\mathrm{3}}{\mathrm{2}}\right\} \\ $$
