
Question Number 114447 by bemath last updated on 19/Sep/20
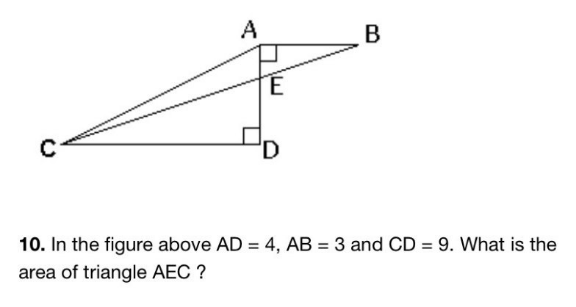
Commented by bemath last updated on 19/Sep/20
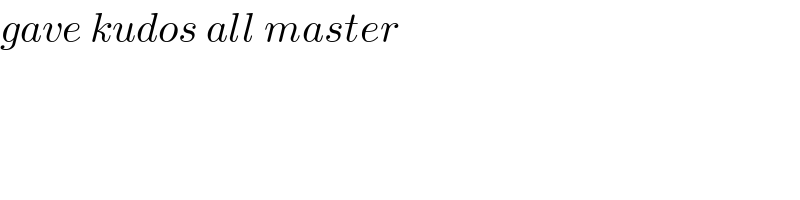
$${gave}\:{kudos}\:{all}\:{master}\: \\ $$
Answered by abdullahquwatan last updated on 19/Sep/20
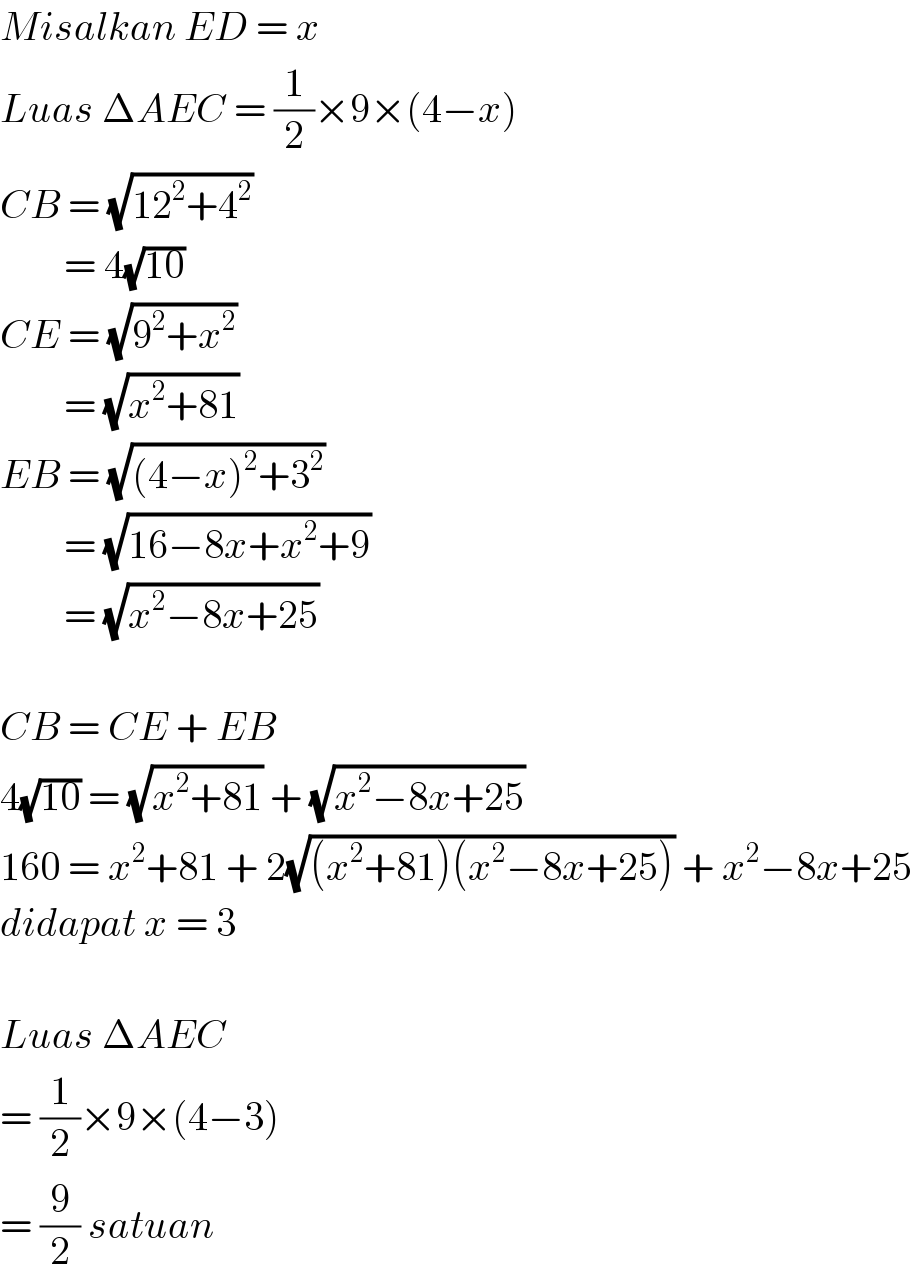
$${Misalkan}\:{ED}\:=\:{x} \\ $$$${Luas}\:\Delta{AEC}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{9}×\left(\mathrm{4}−{x}\right) \\ $$$${CB}\:=\:\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{4}\sqrt{\mathrm{10}} \\ $$$${CE}\:=\:\sqrt{\mathrm{9}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:=\:\sqrt{{x}^{\mathrm{2}} +\mathrm{81}} \\ $$$${EB}\:=\:\sqrt{\left(\mathrm{4}−{x}\right)^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:=\:\sqrt{\mathrm{16}−\mathrm{8}{x}+{x}^{\mathrm{2}} +\mathrm{9}} \\ $$$$\:\:\:\:\:\:\:\:=\:\sqrt{{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{25}} \\ $$$$ \\ $$$${CB}\:=\:{CE}\:+\:{EB} \\ $$$$\mathrm{4}\sqrt{\mathrm{10}}\:=\:\sqrt{{x}^{\mathrm{2}} +\mathrm{81}}\:+\:\sqrt{{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{25}} \\ $$$$\mathrm{160}\:=\:{x}^{\mathrm{2}} +\mathrm{81}\:+\:\mathrm{2}\sqrt{\left({x}^{\mathrm{2}} +\mathrm{81}\right)\left({x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{25}\right)}\:+\:{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{25} \\ $$$${didapat}\:{x}\:=\:\mathrm{3} \\ $$$$ \\ $$$${Luas}\:\Delta{AEC} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{9}×\left(\mathrm{4}−\mathrm{3}\right) \\ $$$$=\:\frac{\mathrm{9}}{\mathrm{2}}\:{satuan} \\ $$
Answered by 1549442205PVT last updated on 19/Sep/20

$$\mathrm{S}_{\mathrm{ABDC}} =\frac{\left(\mathrm{AB}+\mathrm{CD}\right).\mathrm{AD}}{\mathrm{2}}=\frac{\left(\mathrm{3}+\mathrm{9}\right).\mathrm{4}}{\mathrm{2}}=\mathrm{24} \\ $$$$\mathrm{AB}//\mathrm{CD}\:\mathrm{hence}\:\Delta\mathrm{AEB}\simeq\Delta\mathrm{DEC} \\ $$$$\Rightarrow\frac{\mathrm{BE}}{\mathrm{EC}}=\frac{\mathrm{AB}}{\mathrm{CD}}=\frac{\mathrm{3}}{\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}\right) \\ $$$$\Rightarrow\frac{\mathrm{S}_{\mathrm{AEB}} }{\mathrm{S}_{\mathrm{DEC}} }=\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{2}\right) \\ $$$$\mathrm{Since}\:\mathrm{S}_{\mathrm{ACD}} =\mathrm{S}_{\mathrm{BCD}} =\mathrm{m}\left(\mathrm{both}\:\mathrm{triangles}\right. \\ $$$$\mathrm{have}\:\mathrm{common}\:\mathrm{base}\:\mathrm{CD}\:\mathrm{and}\:\mathrm{two}\: \\ $$$$\left.\mathrm{equal}\:\mathrm{altitude}\:\mathrm{from}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{to}\:\mathrm{CD}\right), \\ $$$$\mathrm{S}_{\mathrm{AEC}} =\mathrm{S}_{\mathrm{BED}} =\mathrm{x}\left(\mathrm{both}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{m}−\mathrm{S}_{\mathrm{CDE}} \right) \\ $$$$\mathrm{Put}\:\mathrm{S}_{\mathrm{AEB}} =\mathrm{a},\:\mathrm{from}\:\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{getS}_{\mathrm{DEC}} =\mathrm{9a} \\ $$$$\mathrm{S}_{\mathrm{ABCD}} =\mathrm{24}=\mathrm{9a}+\mathrm{a}+\mathrm{2x}=\mathrm{10a}+\mathrm{2x}\left(\mathrm{3}\right) \\ $$$$\mathrm{We}\:\mathrm{have}\:\frac{\mathrm{S}_{\mathrm{AEC}} }{\mathrm{S}_{\mathrm{AEB}} }=\frac{\mathrm{CE}}{\mathrm{EB}}=\mathrm{3}\left(\mathrm{followsfrom}\left(\mathrm{1}\right)\right) \\ $$$$\Rightarrow\mathrm{S}_{\mathrm{AEC}} =\mathrm{x}=\mathrm{3a}.\mathrm{Replace}\:\mathrm{into}\:\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{24}=\mathrm{10a}+\mathrm{2}.\mathrm{3a}=\mathrm{16a}\Rightarrow\mathrm{a}=\mathrm{24}/\mathrm{16}=\mathrm{1}.\mathrm{5} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{3a}=\mathrm{4}.\mathrm{5} \\ $$$$\mathrm{Thus},\mathrm{S}_{\mathrm{AEC}} =\mathrm{4}.\mathrm{5} \\ $$
Answered by mr W last updated on 19/Sep/20
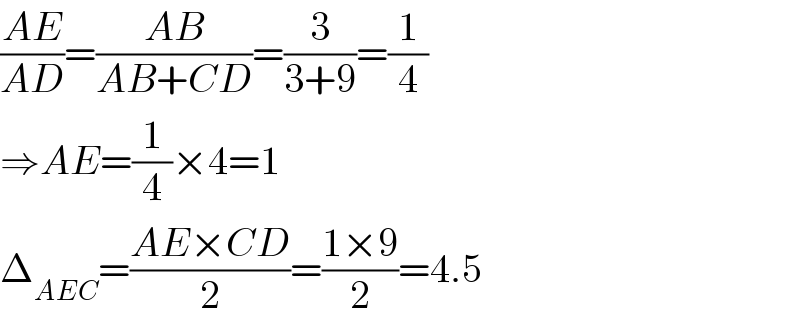
$$\frac{{AE}}{{AD}}=\frac{{AB}}{{AB}+{CD}}=\frac{\mathrm{3}}{\mathrm{3}+\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{AE}=\frac{\mathrm{1}}{\mathrm{4}}×\mathrm{4}=\mathrm{1} \\ $$$$\Delta_{{AEC}} =\frac{{AE}×{CD}}{\mathrm{2}}=\frac{\mathrm{1}×\mathrm{9}}{\mathrm{2}}=\mathrm{4}.\mathrm{5} \\ $$
Answered by Aziztisffola last updated on 19/Sep/20
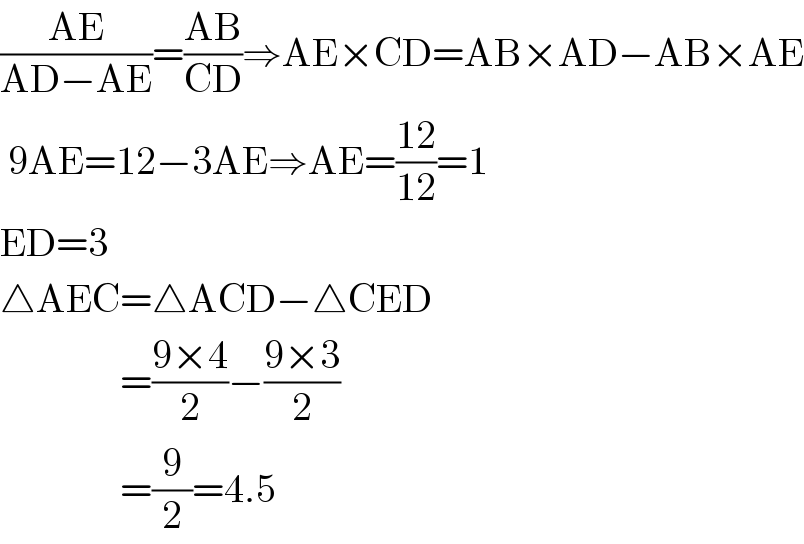
$$\frac{\mathrm{AE}}{\mathrm{AD}−\mathrm{AE}}=\frac{\mathrm{AB}}{\mathrm{CD}}\Rightarrow\mathrm{AE}×\mathrm{CD}=\mathrm{AB}×\mathrm{AD}−\mathrm{AB}×\mathrm{AE} \\ $$$$\:\mathrm{9AE}=\mathrm{12}−\mathrm{3AE}\Rightarrow\mathrm{AE}=\frac{\mathrm{12}}{\mathrm{12}}=\mathrm{1} \\ $$$$\mathrm{ED}=\mathrm{3} \\ $$$$\bigtriangleup\mathrm{AEC}=\bigtriangleup\mathrm{ACD}−\bigtriangleup\mathrm{CED} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{9}×\mathrm{4}}{\mathrm{2}}−\frac{\mathrm{9}×\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{4}.\mathrm{5} \\ $$
