
Question Number 11433 by FilupS last updated on 26/Mar/17
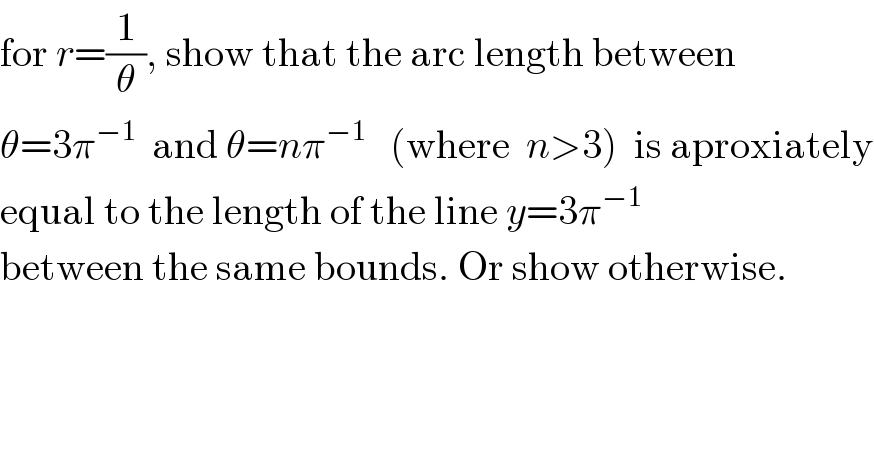
$$\mathrm{for}\:{r}=\frac{\mathrm{1}}{\theta},\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{arc}\:\mathrm{length}\:\mathrm{between} \\ $$ $$\theta=\mathrm{3}\pi^{−\mathrm{1}} \:\:\mathrm{and}\:\theta={n}\pi^{−\mathrm{1}} \:\:\:\left(\mathrm{where}\:\:{n}>\mathrm{3}\right)\:\:\mathrm{is}\:\mathrm{aproxiately} \\ $$ $$\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:{y}=\mathrm{3}\pi^{−\mathrm{1}} \\ $$ $$\mathrm{between}\:\mathrm{the}\:\mathrm{same}\:\mathrm{bounds}.\:\mathrm{Or}\:\mathrm{show}\:\mathrm{otherwise}. \\ $$ $$ \\ $$
Commented byFilupS last updated on 26/Mar/17
Commented by@ANTARES_VY last updated on 26/Mar/17

$$\boldsymbol{\mathrm{what}}\:\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{name}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{program}}.. \\ $$
Commented byFilupS last updated on 26/Mar/17

$$\mathrm{desmos} \\ $$
Commented bymrW1 last updated on 26/Mar/17
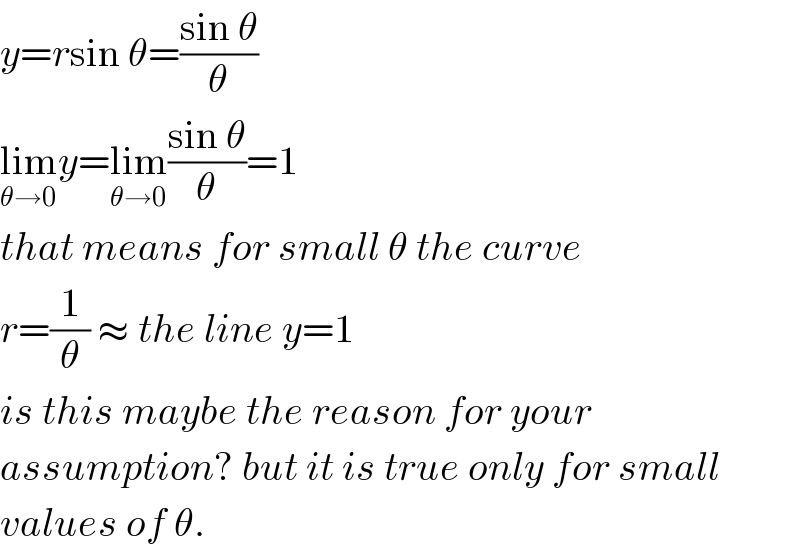
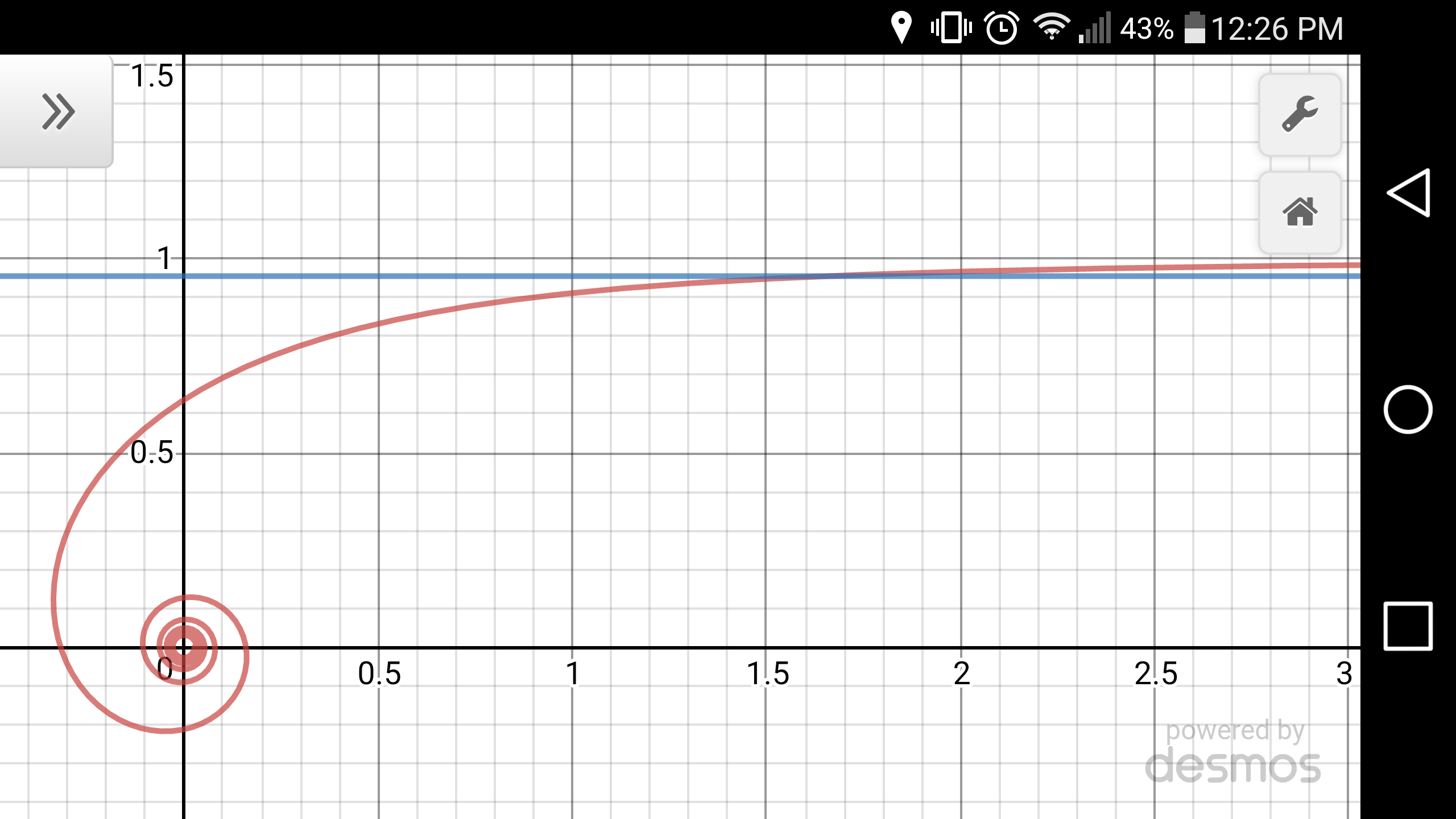
$${y}={r}\mathrm{sin}\:\theta=\frac{\mathrm{sin}\:\theta}{\theta} \\ $$ $$\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}{y}=\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\theta}{\theta}=\mathrm{1} \\ $$ $${that}\:{means}\:{for}\:{small}\:\theta\:{the}\:{curve} \\ $$ $${r}=\frac{\mathrm{1}}{\theta}\:\approx\:{the}\:{line}\:{y}=\mathrm{1} \\ $$ $${is}\:{this}\:{maybe}\:{the}\:{reason}\:{for}\:{your} \\ $$ $${assumption}?\:{but}\:{it}\:{is}\:{true}\:{only}\:{for}\:{small} \\ $$ $${values}\:{of}\:\theta. \\ $$
Commented byFilupS last updated on 26/Mar/17
$$\mathrm{This}\:\mathrm{makes}\:\mathrm{sense}!\:\mathrm{Thanks} \\ $$
Answered by mrW1 last updated on 26/Mar/17
![curve r=(1/θ): (dr/dθ)=−(1/θ^2 ) (√(r^2 +((dr/dθ))^2 ))=(√((1/θ^2 )+(1/θ^4 )))=((√(1+θ^2 ))/θ^2 ) L=∫_θ_1 ^θ_2 (√(r^2 +((dr/dθ))^2 ))dθ=∫_θ_1 ^θ_2 ((√(1+θ^2 ))/θ^2 )dθ [−((√(1+θ^2 ))/θ)+ln (θ+(√(1+θ^2 )))]_θ_1 ^θ_2 =[((√(1+θ_1 ^2 ))/θ_1 )−((√(1+θ_2 ^2 ))/θ_2 )+ln (((ϑ_2 +(√(1+θ_2 ^2 )))/(θ_1 +(√(1+θ_1 ^2 )))))] with θ_1 =3π^(−1) and θ_2 =nπ^(−1) line y=3π^(−1) : ⇒x=y×cot θ=3π^(−1) cot θ x_1 =3π^(−1) cot θ_1 x_2 =3π^(−1) cot θ_2 L_1 =∣∫_x_1 ^x_2 (√(1+(y′)^2 ))dx∣=∣∫_x_1 ^x_2 dx∣=x_1 −x_2 =3π^(−1) (cot θ_1 −cot θ_2 ) =3π^(−1) [cot (3π^(−1) )−cot (nπ^(−1) )] L≠L_1](Q11448.png)
$${curve}\:{r}=\frac{\mathrm{1}}{\theta}: \\ $$ $$\frac{{dr}}{{d}\theta}=−\frac{\mathrm{1}}{\theta^{\mathrm{2}} } \\ $$ $$\sqrt{{r}^{\mathrm{2}} +\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} }=\sqrt{\frac{\mathrm{1}}{\theta^{\mathrm{2}} }+\frac{\mathrm{1}}{\theta^{\mathrm{4}} }}=\frac{\sqrt{\mathrm{1}+\theta^{\mathrm{2}} }}{\theta^{\mathrm{2}} } \\ $$ $${L}=\int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \sqrt{{r}^{\mathrm{2}} +\left(\frac{{dr}}{{d}\theta}\right)^{\mathrm{2}} }{d}\theta=\int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \frac{\sqrt{\mathrm{1}+\theta^{\mathrm{2}} }}{\theta^{\mathrm{2}} }{d}\theta \\ $$ $$\left[−\frac{\sqrt{\mathrm{1}+\theta^{\mathrm{2}} }}{\theta}+\mathrm{ln}\:\left(\theta+\sqrt{\mathrm{1}+\theta^{\mathrm{2}} }\right)\right]_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{2}} } \\ $$ $$=\left[\frac{\sqrt{\mathrm{1}+\theta_{\mathrm{1}} ^{\mathrm{2}} }}{\theta_{\mathrm{1}} }−\frac{\sqrt{\mathrm{1}+\theta_{\mathrm{2}} ^{\mathrm{2}} }}{\theta_{\mathrm{2}} }+\mathrm{ln}\:\left(\frac{\vartheta_{\mathrm{2}} +\sqrt{\mathrm{1}+\theta_{\mathrm{2}} ^{\mathrm{2}} }}{\theta_{\mathrm{1}} +\sqrt{\mathrm{1}+\theta_{\mathrm{1}} ^{\mathrm{2}} }}\right)\right] \\ $$ $${with}\:\theta_{\mathrm{1}} =\mathrm{3}\pi^{−\mathrm{1}} \:{and}\:\theta_{\mathrm{2}} ={n}\pi^{−\mathrm{1}} \\ $$ $$ \\ $$ $$ \\ $$ $${line}\:{y}=\mathrm{3}\pi^{−\mathrm{1}} : \\ $$ $$\Rightarrow{x}={y}×\mathrm{cot}\:\theta=\mathrm{3}\pi^{−\mathrm{1}} \mathrm{cot}\:\theta \\ $$ $${x}_{\mathrm{1}} =\mathrm{3}\pi^{−\mathrm{1}} \mathrm{cot}\:\theta_{\mathrm{1}} \\ $$ $${x}_{\mathrm{2}} =\mathrm{3}\pi^{−\mathrm{1}} \mathrm{cot}\:\theta_{\mathrm{2}} \\ $$ $${L}_{\mathrm{1}} =\mid\int_{{x}_{\mathrm{1}} } ^{{x}_{\mathrm{2}} } \sqrt{\mathrm{1}+\left({y}'\right)^{\mathrm{2}} }{dx}\mid=\mid\int_{{x}_{\mathrm{1}} } ^{{x}_{\mathrm{2}} } {dx}\mid={x}_{\mathrm{1}} −{x}_{\mathrm{2}} \\ $$ $$=\mathrm{3}\pi^{−\mathrm{1}} \left(\mathrm{cot}\:\theta_{\mathrm{1}} −\mathrm{cot}\:\theta_{\mathrm{2}} \right) \\ $$ $$=\mathrm{3}\pi^{−\mathrm{1}} \left[\mathrm{cot}\:\left(\mathrm{3}\pi^{−\mathrm{1}} \right)−\mathrm{cot}\:\left({n}\pi^{−\mathrm{1}} \right)\right] \\ $$ $$ \\ $$ $${L}\neq{L}_{\mathrm{1}} \\ $$
Commented bymrW1 last updated on 26/Mar/17
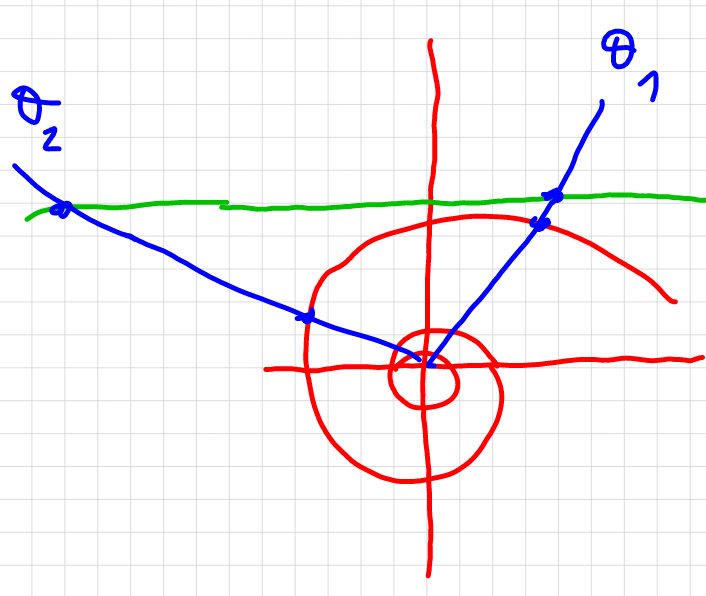
Commented byajfour last updated on 26/Mar/17
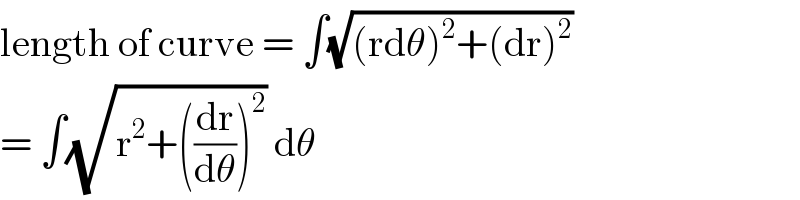
$$\mathrm{length}\:\mathrm{of}\:\mathrm{curve}\:=\:\int\sqrt{\left(\mathrm{rd}\theta\right)^{\mathrm{2}} +\left(\mathrm{dr}\right)^{\mathrm{2}} } \\ $$ $$=\:\int\sqrt{\mathrm{r}^{\mathrm{2}} +\left(\frac{\mathrm{dr}}{\mathrm{d}\theta}\right)^{\mathrm{2}} }\:\mathrm{d}\theta \\ $$
Commented bymrW1 last updated on 26/Mar/17

$${I}=\int\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} }{dx} \\ $$ $${u}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$ $${u}'=\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$ $${v}=−\frac{\mathrm{1}}{{x}} \\ $$ $${v}^{'} =\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$ $${I}=\int{uv}'{dx}={uv}−\int{vu}'{dx} \\ $$ $$=−\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}+\int\frac{{xdx}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$ $$=−\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}+\int\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$ $$=−\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}+\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)+{C} \\ $$
Commented bymrW1 last updated on 26/Mar/17

$${you}\:{are}\:{right}! \\ $$
Commented byajfour last updated on 26/Mar/17
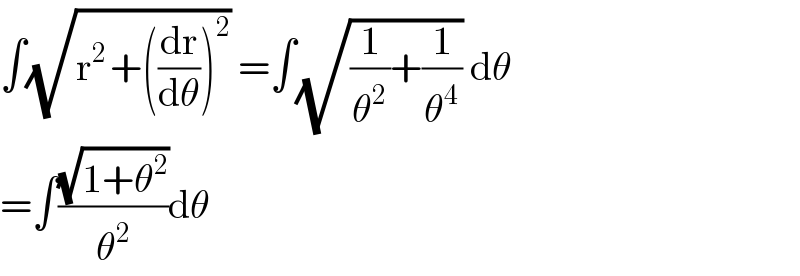
$$\int\sqrt{\mathrm{r}^{\mathrm{2}\:} +\left(\frac{\mathrm{dr}}{\mathrm{d}\theta}\right)^{\mathrm{2}} }\:=\int\sqrt{\frac{\mathrm{1}}{\theta^{\mathrm{2}} }+\frac{\mathrm{1}}{\theta^{\mathrm{4}} }}\:\mathrm{d}\theta \\ $$ $$=\int\frac{\sqrt{\mathrm{1}+\theta^{\mathrm{2}} }}{\theta^{\mathrm{2}} }\mathrm{d}\theta \\ $$
Commented byajfour last updated on 26/Mar/17
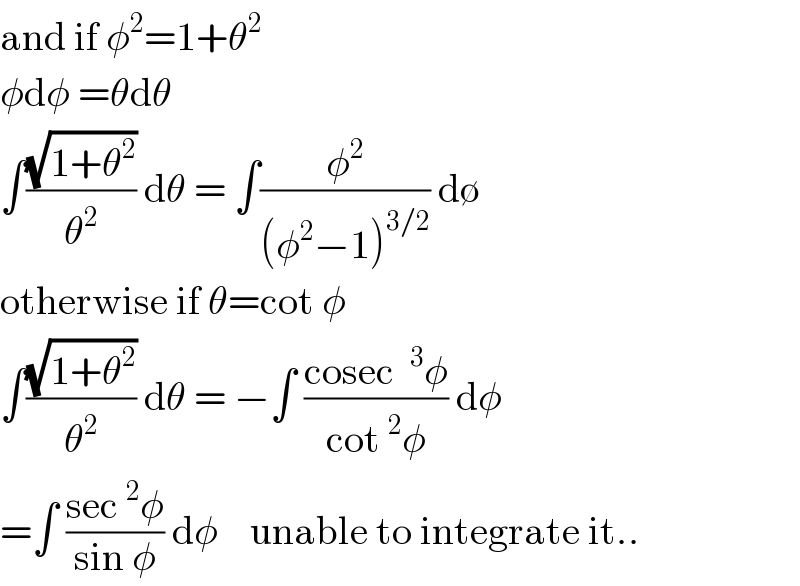
$$\mathrm{and}\:\mathrm{if}\:\phi^{\mathrm{2}} =\mathrm{1}+\theta^{\mathrm{2}} \\ $$ $$\phi\mathrm{d}\phi\:=\theta\mathrm{d}\theta \\ $$ $$\int\frac{\sqrt{\mathrm{1}+\theta^{\mathrm{2}} }}{\theta^{\mathrm{2}} }\:\mathrm{d}\theta\:=\:\int\frac{\phi^{\mathrm{2}} }{\left(\phi^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }\:\mathrm{d}\emptyset \\ $$ $$\mathrm{otherwise}\:\mathrm{if}\:\theta=\mathrm{cot}\:\phi \\ $$ $$\int\frac{\sqrt{\mathrm{1}+\theta^{\mathrm{2}} }}{\theta^{\mathrm{2}} }\:\mathrm{d}\theta\:=\:−\int\:\frac{\mathrm{cosec}\:\:^{\mathrm{3}} \phi}{\mathrm{cot}\:^{\mathrm{2}} \phi}\:\mathrm{d}\phi \\ $$ $$=\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \phi}{\mathrm{sin}\:\phi}\:\mathrm{d}\phi\:\:\:\:\mathrm{unable}\:\mathrm{to}\:\mathrm{integrate}\:\mathrm{it}.. \\ $$
